
Ehresmann connection
Encyclopedia
In differential geometry, an Ehresmann connection (after the French mathematician Charles Ehresmann
who first formalized this concept) is a version of the notion of a connection
, which makes sense on any smooth fibre bundle. In particular, it does not rely on the possible vector bundle structure of the underlying fibre bundle, but nevertheless, linear connections
may be viewed as a special case. Another important special case of Ehresmann connections are principal connections
on principal bundle
s, which are required to be equivariant
in the principal Lie group
action.
in differential geometry is a linear differential operator which takes the directional derivative
of a section of a vector bundle
in a covariant manner. It also allows one to formulate a notion of a parallel
section of a bundle in the direction of a vector: a section s is parallel along a vector X if ∇Xs = 0. So a covariant derivative provides at least two things: a differential operator, and a notion of what it means to be parallel in each direction. An Ehresmann connection drops the differential operator completely and defines a connection axiomatically in terms of the sections parallel in each direction . Specifically, an Ehresmann connection singles out a vector subspace of each tangent space
to the total space of the fibre bundle, called the horizontal space. A section s is then horizontal (i.e., parallel) in the direction X if ds(X) lies in a horizontal space. Here we are regarding s as a function s : M → E from the base M to the fibre bundle E, so that ds : TM → s*TE is then the pushforward of tangent vectors. The horizontal spaces together form a vector subbundle of TE.
This has the immediate benefit of being definable on a much broader class of structures than mere vector bundles. In particular, it is well-defined on a general fibre bundle. Furthermore, many of the features of the covariant derivative still remain: parallel transport, curvature
, and holonomy
.
The missing ingredient of the connection, apart from linearity, is covariance. With the classical covariant derivatives, covariance is an a posteriori feature of the derivative. In their construction one specifies the transformation law of the Christoffel symbols
— which is not covariant — and then general covariance of the derivative follows as a result. For an Ehresmann connection, it is possible to impose a generalized covariance principle from the beginning by introducing a Lie group
acting on the fibres of the fibre bundle. The appropriate condition is to require that the horizontal spaces be, in a certain sense, equivariant
with respect to the group action.
The final finishing touch for an Ehresmann connection is that it can be represented as a differential form
, in much the same way as the case of a connection form
. If the group acts on the fibres and the connection is equivariant, then the form will also be equivariant. Furthermore, the connection form allows for a definition of curvature as a curvature form
as well.
. Let V = ker (dπ : TE → π*TM) be the vertical bundle
consisting of the vectors tangent to the fibres E, so that the fibre of V at e∈E is Te(Eπ(e)).
of the connection, which is complementary to V, in the sense that it defines a direct sum decomposition TE = H⊕V . In more detail, the horizontal bundle has the following properties.
In more sophisticated terms, such an assignment of horizontal spaces satisfying these properties corresponds precisely to a smooth section of the jet bundle
J1E → E.
of the Ehresmann connection. Thus v is a vector bundle homomorphism from TE to itself with the following properties:
Conversely, if v is a vector bundle endomorphism
of TE satisfying these two properties, then H = ker v is the horizontal subbundle of an Ehresmann connection.
Finally, note that v, being a linear mapping of each tangent space into itself, may also be regarded as a TE-valued 1-form. This will be a useful perspective in sections to come.
for other versions of the connection formalism.
Specifically, suppose that γ(t) is a smooth curve in M through the point x = γ(0). Let e ∈ Ex be a point in the fibre over x. A lift of γ through e is a curve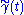 in the total space E such that
in the total space E such that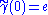 , and
, and 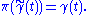
A lift is horizontal if, in addition, every tangent of the curve lies in the horizontal subbundle of TE: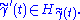
It can be shown using the rank-nullity theorem
applied to π and v that each vector X∈TxM has a unique horizontal lift to a vector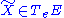 . In particular, the tangent field to γ generates a horizontal vector field in the total space of the pullback bundle
. In particular, the tangent field to γ generates a horizontal vector field in the total space of the pullback bundle
γ*E. By the Picard–Lindelöf theorem, this vector field is integrable. Thus, for any curve γ and point e over x = γ(0), there exists a unique horizontal lift of γ through e for small time t.
Note that, for general Ehresmann connections, the horizontal lift is path-dependent. When two smooth curves in M, coinciding at γ1(0) = γ2(0) = x0 and also intersecting at another point x1 ∈ M, are lifted horizontally to E through the same e ∈ π−1(x0), they will generally pass through different points of π−1(x1). This has important consequences for the differential geometry of fibre bundles: the space of sections of H is not a Lie subalgebra of the space of vector fields on E, because it is not (in general) closed under the Lie bracket of vector fields
. This failure of closure under Lie bracket is measured by the curvature.

where [-,-] denotes the Frölicher-Nijenhuis bracket
of v ∈ Ω1(E,TE) with itself. Thus R ∈ Ω2(E,TE) is the two-form on E with values in TE defined by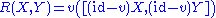 ,
,
or, in other terms,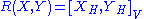 ,
,
where X = XH + XV denotes the direct sum decomposition into H and V components, respectively. From this last expression for the curvature, it is seen to vanish identically if, and only if, the horizontal subbundle is Frobenius integrable. Thus the curvature is the integrability condition for the horizontal subbundle to yield transverse sections of the fibre bundle E → M.
The curvature of an Ehresmann connection also satisfies a version of the Bianchi identity: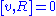
where again [-,-] is the Frölicher-Nijenhuis bracket of v ∈ Ω1(E,TE) and R ∈ Ω2(E,TE).
. For a complete Ehresmann connection, a curve can be horizontally lifted over its entire domain.
of the connection.
over M. Then an Ehresmann connection H on E is said to be a principal (Ehresmann) connection if it is invariant with respect to the G action on E in the sense that for any e∈E and g∈G; here
for any e∈E and g∈G; here 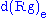 denotes the differential of the right action
denotes the differential of the right action
of g on E at e.
The one-parameter subgroups of G act vertically on E. The differential of this action allows one to identify the subspace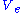 with the Lie algebra g of group G, say by map
with the Lie algebra g of group G, say by map  . The connection form v of the Ehresmann connection may then be viewed as a 1-form ω on E with values in g defined by ω(X)=ι(v(X)).
. The connection form v of the Ehresmann connection may then be viewed as a 1-form ω on E with values in g defined by ω(X)=ι(v(X)).
Thus reinterpreted, the connection form ω satisfies the following two properties:
Conversely, it can be shown that such a g-valued 1-form on a principal bundle generates a horizontal distribution satisfying the aforementioned properties.
Given a local trivialization one can reduce ω to the horizontal vector fields (in this trivialization). It defines a 1-form ω' on B via pullback. The form ω determines ω completely, but it depends on the choice of trivialization. (This form is often also called a connection form
and denoted simply by ω.)
over M. Then an Ehresmann connection H on E is said to be a linear (Ehresmann) connection if He depends linearly on e ∈ Ex for each x ∈ M. To make this precise, let Sλ denote scalar multiplication by λ on E, and let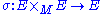 denote addition.
denote addition.
Then H is linear if and only if for all x ∈ M, the following properties are satisfied. 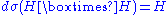 where
where 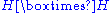 denotes the corresponding horizontal subbundle on
denotes the corresponding horizontal subbundle on 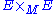 .
.
Since E is a vector bundle, its vertical bundle V is isomorphic to π*E. Therefore if s is a section of E, then
v(ds):TM→s*V=s*π*E=E. The fact that the Ehresmann connection is linear implies that this is a vector bundle homomorphism, and is therefore given by a section ∇s of the vector bundle Hom(TM,E), called the covariant derivative of s.
Conversely a covariant derivative
∇ on a vector bundle defines a linear Ehresmann connection by defining He, for e ∈ E with x=π(e), to be the image dsx(TxM) where s is a section of E with ∇Xs=0 for all X ∈ TxM.
Note that (for historical reasons) the term linear when applied to connections, is sometimes used (like the word affine — see Affine connection
) to refer to connections defined on the tangent bundle or frame bundle
.
. For instance, a (linear) connection in a vector bundle
E, thought of giving a parallelism of E as above, induces a connection on the associated bundle of frames PE of E. Conversely, a connection in PE gives rise to a (linear) connection in E provided that the connection in PE is equivariant with respect to the action of the general linear group on the frames (and thus a principal connection
). It is not always possible for an Ehresmann connection to induce, in a natural way, a connection on an associated bundle. For example, a non-equivariant Ehresmann connection on a bundle of frames of a vector bundle may not induce a connection on the vector bundle.
Suppose that E is an associated bundle of P, so that E = P ×G F. A G-connection on E is an Ehresmann connection such that the parallel transport map τ : Fx → Fx′ is given by a G-transformation of the fibres (over sufficiently nearby points x and x′ in M joined by a curve).
Given a principal connection on P, one obtains a G-connection on the associated fibre bundle E = P ×G F via pullback.
Conversely, given a G-connection on E it is possible to recover the principal connection on the associated principal bundle P. To recover this principal connection, one introduces the notion of a frame on the typical fibre F. Since G is a finite-dimensional Lie group acting effectively on F, there must exist a finite configuration of points (y1,...,ym) within F such that the G-orbit R = {(gy1,...,gym) | g ∈ G} is a principal homogeneous space of G. One can think of R as giving a generalization of the notion of a frame for the G-action on F. Note that, since R is a principal homogeneous space for G, the fibre bundle E(R) associated to E with typical fibre R is (equivalent to) the principal bundle associated to E. But it is also a subbundle of the m-fold product bundle of E with itself. The distribution of horizontal spaces on E induces a distribution of spaces on this product bundle. Since the parallel transport maps associated to the connection are G-maps, they preserve the subspace E(R), and so the G-connection descends to a principal G-connection on E(R).
In summary, there is a one-to-one correspondence (up to equivalence) between the descents of principal connections to associated fibre bundles, and G-connections on associated fibre bundles. For this reason, in the category of fibre bundles with a structure group G, the principal connection contains all relevant information for G-connections on the associated bundles. Hence, unless there is an overriding reason to consider connections on associated bundles (as there is, for instance, in the case of Cartan connection
s) one usually works directly with the principal connection.
Charles Ehresmann
Charles Ehresmann was a French mathematician who worked on differential topology and category theory. He is known for work on the topology of Lie groups, the jet concept , and his seminar on category theory.He attended the École Normale Supérieure in Paris before performing one year of military...
who first formalized this concept) is a version of the notion of a connection
Connection (mathematics)
In geometry, the notion of a connection makes precise the idea of transporting data along a curve or family of curves in a parallel and consistent manner. There are a variety of kinds of connections in modern geometry, depending on what sort of data one wants to transport...
, which makes sense on any smooth fibre bundle. In particular, it does not rely on the possible vector bundle structure of the underlying fibre bundle, but nevertheless, linear connections
Connection (vector bundle)
In mathematics, a connection on a fiber bundle is a device that defines a notion of parallel transport on the bundle; that is, a way to "connect" or identify fibers over nearby points. If the fiber bundle is a vector bundle, then the notion of parallel transport is required to be linear...
may be viewed as a special case. Another important special case of Ehresmann connections are principal connections
Connection (principal bundle)
In mathematics, a connection is a device that defines a notion of parallel transport on the bundle; that is, a way to "connect" or identify fibers over nearby points...
on principal bundle
Principal bundle
In mathematics, a principal bundle is a mathematical object which formalizes some of the essential features of the Cartesian product X × G of a space X with a group G...
s, which are required to be equivariant
Equivariant
In mathematics, an equivariant map is a function between two sets that commutes with the action of a group. Specifically, let G be a group and let X and Y be two associated G-sets. A function f : X → Y is said to be equivariant iffor all g ∈ G and all x in X...
in the principal Lie group
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
action.
Introduction
A covariant derivativeConnection (vector bundle)
In mathematics, a connection on a fiber bundle is a device that defines a notion of parallel transport on the bundle; that is, a way to "connect" or identify fibers over nearby points. If the fiber bundle is a vector bundle, then the notion of parallel transport is required to be linear...
in differential geometry is a linear differential operator which takes the directional derivative
Directional derivative
In mathematics, the directional derivative of a multivariate differentiable function along a given vector V at a given point P intuitively represents the instantaneous rate of change of the function, moving through P in the direction of V...
of a section of a vector bundle
Vector bundle
In mathematics, a vector bundle is a topological construction that makes precise the idea of a family of vector spaces parameterized by another space X : to every point x of the space X we associate a vector space V in such a way that these vector spaces fit together...
in a covariant manner. It also allows one to formulate a notion of a parallel
Parallel transport
In geometry, parallel transport is a way of transporting geometrical data along smooth curves in a manifold. If the manifold is equipped with an affine connection , then this connection allows one to transport vectors of the manifold along curves so that they stay parallel with respect to the...
section of a bundle in the direction of a vector: a section s is parallel along a vector X if ∇Xs = 0. So a covariant derivative provides at least two things: a differential operator, and a notion of what it means to be parallel in each direction. An Ehresmann connection drops the differential operator completely and defines a connection axiomatically in terms of the sections parallel in each direction . Specifically, an Ehresmann connection singles out a vector subspace of each tangent space
Tangent space
In mathematics, the tangent space of a manifold facilitates the generalization of vectors from affine spaces to general manifolds, since in the latter case one cannot simply subtract two points to obtain a vector pointing from one to the other....
to the total space of the fibre bundle, called the horizontal space. A section s is then horizontal (i.e., parallel) in the direction X if ds(X) lies in a horizontal space. Here we are regarding s as a function s : M → E from the base M to the fibre bundle E, so that ds : TM → s*TE is then the pushforward of tangent vectors. The horizontal spaces together form a vector subbundle of TE.
This has the immediate benefit of being definable on a much broader class of structures than mere vector bundles. In particular, it is well-defined on a general fibre bundle. Furthermore, many of the features of the covariant derivative still remain: parallel transport, curvature
Curvature
In mathematics, curvature refers to any of a number of loosely related concepts in different areas of geometry. Intuitively, curvature is the amount by which a geometric object deviates from being flat, or straight in the case of a line, but this is defined in different ways depending on the context...
, and holonomy
Holonomy
In differential geometry, the holonomy of a connection on a smooth manifold is a general geometrical consequence of the curvature of the connection measuring the extent to which parallel transport around closed loops fails to preserve the geometrical data being transported. For flat connections,...
.
The missing ingredient of the connection, apart from linearity, is covariance. With the classical covariant derivatives, covariance is an a posteriori feature of the derivative. In their construction one specifies the transformation law of the Christoffel symbols
Christoffel symbols
In mathematics and physics, the Christoffel symbols, named for Elwin Bruno Christoffel , are numerical arrays of real numbers that describe, in coordinates, the effects of parallel transport in curved surfaces and, more generally, manifolds. As such, they are coordinate-space expressions for the...
— which is not covariant — and then general covariance of the derivative follows as a result. For an Ehresmann connection, it is possible to impose a generalized covariance principle from the beginning by introducing a Lie group
Lie group
In mathematics, a Lie group is a group which is also a differentiable manifold, with the property that the group operations are compatible with the smooth structure...
acting on the fibres of the fibre bundle. The appropriate condition is to require that the horizontal spaces be, in a certain sense, equivariant
Equivariant
In mathematics, an equivariant map is a function between two sets that commutes with the action of a group. Specifically, let G be a group and let X and Y be two associated G-sets. A function f : X → Y is said to be equivariant iffor all g ∈ G and all x in X...
with respect to the group action.
The final finishing touch for an Ehresmann connection is that it can be represented as a differential form
Differential form
In the mathematical fields of differential geometry and tensor calculus, differential forms are an approach to multivariable calculus that is independent of coordinates. Differential forms provide a better definition for integrands in calculus...
, in much the same way as the case of a connection form
Connection form
In mathematics, and specifically differential geometry, a connection form is a manner of organizing the data of a connection using the language of moving frames and differential forms....
. If the group acts on the fibres and the connection is equivariant, then the form will also be equivariant. Furthermore, the connection form allows for a definition of curvature as a curvature form
Curvature form
In differential geometry, the curvature form describes curvature of a connection on a principal bundle. It can be considered as an alternative to or generalization of curvature tensor in Riemannian geometry.-Definition:...
as well.
Formal definition
Let π: E → M be a smooth fiber bundleFiber bundle
In mathematics, and particularly topology, a fiber bundle is intuitively a space which locally "looks" like a certain product space, but globally may have a different topological structure...
. Let V = ker (dπ : TE → π*TM) be the vertical bundle
Vertical bundle
The vertical bundle of a smooth fiber bundle is the subbundle of the tangent bundle that consists of all vectors which are tangent to the fibers...
consisting of the vectors tangent to the fibres E, so that the fibre of V at e∈E is Te(Eπ(e)).
Definition via horizontal subspaces
An Ehresmann connection on E is a smooth subbundle H of TE, called the horizontal bundleHorizontal bundle
In mathematics, in the field of differential topology, givena smooth fiber bundle over a smooth manifold M, then the vertical bundle VE of E is the subbundle of the tangent bundle TE consisting of the vectors which are tangent to the fibers of E over M...
of the connection, which is complementary to V, in the sense that it defines a direct sum decomposition TE = H⊕V . In more detail, the horizontal bundle has the following properties.
- For each point e ∈ E, He is a vector subspaceVector spaceA vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
of the tangent space TeE to E at e, called the horizontal subspace of the connection at e. - He depends smoothly on e.
- For each e ∈ E, He ∩ Ve = {0}.
- Any tangent vector in TeE (for any e∈E) is the sum of a horizontal and vertical component, so that TeE = He + Ve.
In more sophisticated terms, such an assignment of horizontal spaces satisfying these properties corresponds precisely to a smooth section of the jet bundle
Jet bundle
In differential geometry, the jet bundle is a certain construction which makes a new smooth fiber bundle out of a given smooth fiber bundle. It makes it possible to write differential equations on sections of a fiber bundle in an invariant form...
J1E → E.
Definition via a connection form
Equivalently, let v be the projection onto the vertical bundle V along H (so that H = ker v). This is determined by the above direct sum decomposition of TE into horizontal and vertical parts and is sometimes called the connection formConnection form
In mathematics, and specifically differential geometry, a connection form is a manner of organizing the data of a connection using the language of moving frames and differential forms....
of the Ehresmann connection. Thus v is a vector bundle homomorphism from TE to itself with the following properties:
- v2 = v;
- The image of v is V.
Conversely, if v is a vector bundle endomorphism
Endomorphism
In mathematics, an endomorphism is a morphism from a mathematical object to itself. For example, an endomorphism of a vector space V is a linear map ƒ: V → V, and an endomorphism of a group G is a group homomorphism ƒ: G → G. In general, we can talk about...
of TE satisfying these two properties, then H = ker v is the horizontal subbundle of an Ehresmann connection.
Finally, note that v, being a linear mapping of each tangent space into itself, may also be regarded as a TE-valued 1-form. This will be a useful perspective in sections to come.
Parallel transport via horizontal lifts
An Ehresmann connection also prescribes a manner for lifting curves from the base manifold M into the total space of the fibre bundle E so that the tangents to the curve are horizontal. These horizontal lifts are a direct analogue of parallel transportParallel transport
In geometry, parallel transport is a way of transporting geometrical data along smooth curves in a manifold. If the manifold is equipped with an affine connection , then this connection allows one to transport vectors of the manifold along curves so that they stay parallel with respect to the...
for other versions of the connection formalism.
Specifically, suppose that γ(t) is a smooth curve in M through the point x = γ(0). Let e ∈ Ex be a point in the fibre over x. A lift of γ through e is a curve
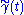 in the total space E such that
in the total space E such that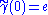 , and
, and 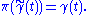
A lift is horizontal if, in addition, every tangent of the curve lies in the horizontal subbundle of TE:
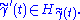
It can be shown using the rank-nullity theorem
Rank-nullity theorem
In mathematics, the rank–nullity theorem of linear algebra, in its simplest form, states that the rank and the nullity of a matrix add up to the number of columns of the matrix. Specifically, if A is an m-by-n matrix over some field, thenThis applies to linear maps as well...
applied to π and v that each vector X∈TxM has a unique horizontal lift to a vector
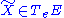 . In particular, the tangent field to γ generates a horizontal vector field in the total space of the pullback bundle
. In particular, the tangent field to γ generates a horizontal vector field in the total space of the pullback bundlePullback bundle
In mathematics, a pullback bundle or induced bundle is a useful construction in the theory of fiber bundles. Given a fiber bundle π : E → B and a continuous map f : B′ → B one can define a "pullback" of E by f as a bundle f*E over B′...
γ*E. By the Picard–Lindelöf theorem, this vector field is integrable. Thus, for any curve γ and point e over x = γ(0), there exists a unique horizontal lift of γ through e for small time t.
Note that, for general Ehresmann connections, the horizontal lift is path-dependent. When two smooth curves in M, coinciding at γ1(0) = γ2(0) = x0 and also intersecting at another point x1 ∈ M, are lifted horizontally to E through the same e ∈ π−1(x0), they will generally pass through different points of π−1(x1). This has important consequences for the differential geometry of fibre bundles: the space of sections of H is not a Lie subalgebra of the space of vector fields on E, because it is not (in general) closed under the Lie bracket of vector fields
Lie derivative
In mathematics, the Lie derivative , named after Sophus Lie by Władysław Ślebodziński, evaluates the change of a vector field or more generally a tensor field, along the flow of another vector field...
. This failure of closure under Lie bracket is measured by the curvature.
Curvature
Let v be an Ehresmann connection. Then the curvature of v is given by
where [-,-] denotes the Frölicher-Nijenhuis bracket
Frölicher-Nijenhuis bracket
In mathematics, the Frölicher–Nijenhuis bracket is an extension of the Lie bracket of vector fields to vector-valued differential forms on a differentiable manifold...
of v ∈ Ω1(E,TE) with itself. Thus R ∈ Ω2(E,TE) is the two-form on E with values in TE defined by
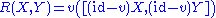 ,
,or, in other terms,
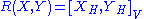 ,
,where X = XH + XV denotes the direct sum decomposition into H and V components, respectively. From this last expression for the curvature, it is seen to vanish identically if, and only if, the horizontal subbundle is Frobenius integrable. Thus the curvature is the integrability condition for the horizontal subbundle to yield transverse sections of the fibre bundle E → M.
The curvature of an Ehresmann connection also satisfies a version of the Bianchi identity:
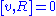
where again [-,-] is the Frölicher-Nijenhuis bracket of v ∈ Ω1(E,TE) and R ∈ Ω2(E,TE).
Completeness
An Ehresmann connection allows curves to have unique horizontal lifts locallyLocal property
In mathematics, a phenomenon is sometimes said to occur locally if, roughly speaking, it occurs on sufficiently small or arbitrarily small neighborhoods of points.-Properties of a single space:...
. For a complete Ehresmann connection, a curve can be horizontally lifted over its entire domain.
Holonomy
Flatness of the connection corresponds locally to the Frobenius integrability of the horizontal spaces. At the other extreme, non-vanishing curvature implies the presence of holonomyHolonomy
In differential geometry, the holonomy of a connection on a smooth manifold is a general geometrical consequence of the curvature of the connection measuring the extent to which parallel transport around closed loops fails to preserve the geometrical data being transported. For flat connections,...
of the connection.
Principal bundles and principal connections
Suppose that E is a smooth principal G-bundlePrincipal bundle
In mathematics, a principal bundle is a mathematical object which formalizes some of the essential features of the Cartesian product X × G of a space X with a group G...
over M. Then an Ehresmann connection H on E is said to be a principal (Ehresmann) connection if it is invariant with respect to the G action on E in the sense that
 for any e∈E and g∈G; here
for any e∈E and g∈G; here 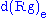 denotes the differential of the right action
denotes the differential of the right actionGroup action
In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
of g on E at e.
The one-parameter subgroups of G act vertically on E. The differential of this action allows one to identify the subspace
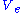 with the Lie algebra g of group G, say by map
with the Lie algebra g of group G, say by map  . The connection form v of the Ehresmann connection may then be viewed as a 1-form ω on E with values in g defined by ω(X)=ι(v(X)).
. The connection form v of the Ehresmann connection may then be viewed as a 1-form ω on E with values in g defined by ω(X)=ι(v(X)).Thus reinterpreted, the connection form ω satisfies the following two properties:
- It transforms equivariantEquivariantIn mathematics, an equivariant map is a function between two sets that commutes with the action of a group. Specifically, let G be a group and let X and Y be two associated G-sets. A function f : X → Y is said to be equivariant iffor all g ∈ G and all x in X...
ly under the G action: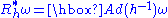 for all h∈G, where Rh* is the pullback under the right action and Ad is the adjoint representationAdjoint representationIn mathematics, the adjoint representation of a Lie group G is the natural representation of G on its own Lie algebra...
for all h∈G, where Rh* is the pullback under the right action and Ad is the adjoint representationAdjoint representationIn mathematics, the adjoint representation of a Lie group G is the natural representation of G on its own Lie algebra...
of G on its Lie algebra. - It maps vertical vector fields to their associated elements of the Lie algebra: ω(X)=ι(X) for all X∈V.
Conversely, it can be shown that such a g-valued 1-form on a principal bundle generates a horizontal distribution satisfying the aforementioned properties.
Given a local trivialization one can reduce ω to the horizontal vector fields (in this trivialization). It defines a 1-form ω' on B via pullback. The form ω determines ω completely, but it depends on the choice of trivialization. (This form is often also called a connection form
Connection form
In mathematics, and specifically differential geometry, a connection form is a manner of organizing the data of a connection using the language of moving frames and differential forms....
and denoted simply by ω.)
Vector bundles and covariant derivatives
Suppose that E is a smooth vector bundleVector bundle
In mathematics, a vector bundle is a topological construction that makes precise the idea of a family of vector spaces parameterized by another space X : to every point x of the space X we associate a vector space V in such a way that these vector spaces fit together...
over M. Then an Ehresmann connection H on E is said to be a linear (Ehresmann) connection if He depends linearly on e ∈ Ex for each x ∈ M. To make this precise, let Sλ denote scalar multiplication by λ on E, and let
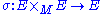 denote addition.
denote addition.Then H is linear if and only if for all x ∈ M, the following properties are satisfied.
-
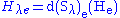 for any
for any
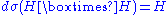 where
where 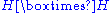 denotes the corresponding horizontal subbundle on
denotes the corresponding horizontal subbundle on 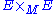 .
.Since E is a vector bundle, its vertical bundle V is isomorphic to π*E. Therefore if s is a section of E, then
v(ds):TM→s*V=s*π*E=E. The fact that the Ehresmann connection is linear implies that this is a vector bundle homomorphism, and is therefore given by a section ∇s of the vector bundle Hom(TM,E), called the covariant derivative of s.
Conversely a covariant derivative
Connection (vector bundle)
In mathematics, a connection on a fiber bundle is a device that defines a notion of parallel transport on the bundle; that is, a way to "connect" or identify fibers over nearby points. If the fiber bundle is a vector bundle, then the notion of parallel transport is required to be linear...
∇ on a vector bundle defines a linear Ehresmann connection by defining He, for e ∈ E with x=π(e), to be the image dsx(TxM) where s is a section of E with ∇Xs=0 for all X ∈ TxM.
Note that (for historical reasons) the term linear when applied to connections, is sometimes used (like the word affine — see Affine connection
Affine connection
In the branch of mathematics called differential geometry, an affine connection is a geometrical object on a smooth manifold which connects nearby tangent spaces, and so permits tangent vector fields to be differentiated as if they were functions on the manifold with values in a fixed vector space...
) to refer to connections defined on the tangent bundle or frame bundle
Frame bundle
In mathematics, a frame bundle is a principal fiber bundle F associated to any vector bundle E. The fiber of F over a point x is the set of all ordered bases, or frames, for Ex...
.
Associated bundles
An Ehresmann connection on a fibre bundle (endowed with a structure group) sometimes gives rise to an Ehresmann connection on an associated bundleAssociated bundle
In mathematics, the theory of fiber bundles with a structure group G allows an operation of creating an associated bundle, in which the typical fiber of a bundle changes from F_1 to F_2, which are both topological spaces with a group action of G...
. For instance, a (linear) connection in a vector bundle
Connection (vector bundle)
In mathematics, a connection on a fiber bundle is a device that defines a notion of parallel transport on the bundle; that is, a way to "connect" or identify fibers over nearby points. If the fiber bundle is a vector bundle, then the notion of parallel transport is required to be linear...
E, thought of giving a parallelism of E as above, induces a connection on the associated bundle of frames PE of E. Conversely, a connection in PE gives rise to a (linear) connection in E provided that the connection in PE is equivariant with respect to the action of the general linear group on the frames (and thus a principal connection
Connection (principal bundle)
In mathematics, a connection is a device that defines a notion of parallel transport on the bundle; that is, a way to "connect" or identify fibers over nearby points...
). It is not always possible for an Ehresmann connection to induce, in a natural way, a connection on an associated bundle. For example, a non-equivariant Ehresmann connection on a bundle of frames of a vector bundle may not induce a connection on the vector bundle.
Suppose that E is an associated bundle of P, so that E = P ×G F. A G-connection on E is an Ehresmann connection such that the parallel transport map τ : Fx → Fx′ is given by a G-transformation of the fibres (over sufficiently nearby points x and x′ in M joined by a curve).
Given a principal connection on P, one obtains a G-connection on the associated fibre bundle E = P ×G F via pullback.
Conversely, given a G-connection on E it is possible to recover the principal connection on the associated principal bundle P. To recover this principal connection, one introduces the notion of a frame on the typical fibre F. Since G is a finite-dimensional Lie group acting effectively on F, there must exist a finite configuration of points (y1,...,ym) within F such that the G-orbit R = {(gy1,...,gym) | g ∈ G} is a principal homogeneous space of G. One can think of R as giving a generalization of the notion of a frame for the G-action on F. Note that, since R is a principal homogeneous space for G, the fibre bundle E(R) associated to E with typical fibre R is (equivalent to) the principal bundle associated to E. But it is also a subbundle of the m-fold product bundle of E with itself. The distribution of horizontal spaces on E induces a distribution of spaces on this product bundle. Since the parallel transport maps associated to the connection are G-maps, they preserve the subspace E(R), and so the G-connection descends to a principal G-connection on E(R).
In summary, there is a one-to-one correspondence (up to equivalence) between the descents of principal connections to associated fibre bundles, and G-connections on associated fibre bundles. For this reason, in the category of fibre bundles with a structure group G, the principal connection contains all relevant information for G-connections on the associated bundles. Hence, unless there is an overriding reason to consider connections on associated bundles (as there is, for instance, in the case of Cartan connection
Cartan connection
In the mathematical field of differential geometry, a Cartan connection is a flexible generalization of the notion of an affine connection. It may also be regarded as a specialization of the general concept of a principal connection, in which the geometry of the principal bundle is tied to the...
s) one usually works directly with the principal connection.
Further reading
- Raoul BottRaoul BottRaoul Bott, FRS was a Hungarian mathematician known for numerous basic contributions to geometry in its broad sense...
(1970) "Topological obstruction to integrability", Proc. Symp. Pure Math., 16 Amer. Math. Soc., Providence, RI.

