
Free particle
Encyclopedia
In physics
, a free particle is a particle that, in some sense, is not bound. In classical physics, this means the particle is present in a "field-free" space.
given by
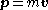
and the energy by
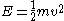
where m is the mass of the particle and v is the vector velocity of the particle.
for a free particle is:
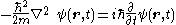
The solution for a particular momentum is given by a plane wave
:
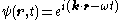
with the constraint
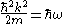
where r is the position vector, t is time, k is the wave vector
, and ω is the angular frequency
. Since the integral of ψψ* over all space must be unity, the wave function must first be normalized. This is a problem for general free particles, but is not a problem for a slightly non-free particle that is somewhat localized in momentum and position. (See particle in a box
for a further discussion.)
The expectation value of the momentum p is
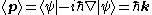
The expectation value of the energy E is
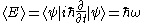
Solving for k and ω and substituting into the constraint equation yields the familiar relationship between energy and momentum for non-relativistic massive particles
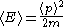
where p=|p|. The group velocity of the wave is defined as
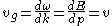
where v is the classical velocity of the particle.
The phase velocity of the wave is defined as
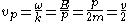
A general free particle need not have a specific momentum or energy. In this case, the free particle wavefunction may be represented by a superposition of free particle momentum eigenfunctions:
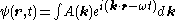
where the integral is over all k-space.
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
, a free particle is a particle that, in some sense, is not bound. In classical physics, this means the particle is present in a "field-free" space.
Classical Free Particle
The classical free particle is characterized simply by a fixed velocity. The momentum isgiven by
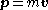
and the energy by
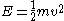
where m is the mass of the particle and v is the vector velocity of the particle.
Non-Relativistic Quantum Free Particle
The Schrödinger equationSchrödinger equation
The Schrödinger equation was formulated in 1926 by Austrian physicist Erwin Schrödinger. Used in physics , it is an equation that describes how the quantum state of a physical system changes in time....
for a free particle is:
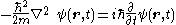
The solution for a particular momentum is given by a plane wave
Plane wave
In the physics of wave propagation, a plane wave is a constant-frequency wave whose wavefronts are infinite parallel planes of constant peak-to-peak amplitude normal to the phase velocity vector....
:
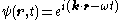
with the constraint
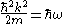
where r is the position vector, t is time, k is the wave vector
Wave vector
In physics, a wave vector is a vector which helps describe a wave. Like any vector, it has a magnitude and direction, both of which are important: Its magnitude is either the wavenumber or angular wavenumber of the wave , and its direction is ordinarily the direction of wave propagation In...
, and ω is the angular frequency
Angular frequency
In physics, angular frequency ω is a scalar measure of rotation rate. Angular frequency is the magnitude of the vector quantity angular velocity...
. Since the integral of ψψ* over all space must be unity, the wave function must first be normalized. This is a problem for general free particles, but is not a problem for a slightly non-free particle that is somewhat localized in momentum and position. (See particle in a box
Particle in a box
In quantum mechanics, the particle in a box model describes a particle free to move in a small space surrounded by impenetrable barriers. The model is mainly used as a hypothetical example to illustrate the differences between classical and quantum systems...
for a further discussion.)
The expectation value of the momentum p is
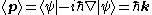
The expectation value of the energy E is
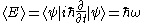
Solving for k and ω and substituting into the constraint equation yields the familiar relationship between energy and momentum for non-relativistic massive particles
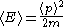
where p=|p|. The group velocity of the wave is defined as
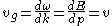
where v is the classical velocity of the particle.
The phase velocity of the wave is defined as
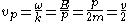
A general free particle need not have a specific momentum or energy. In this case, the free particle wavefunction may be represented by a superposition of free particle momentum eigenfunctions:
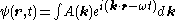
where the integral is over all k-space.
Relativistic free particle
There are a number of equations describing relativistic particles. For a description of the free particle solutions, see the individual articles.- The Klein-Gordon equationKlein-Gordon equationThe Klein–Gordon equation is a relativistic version of the Schrödinger equation....
describes charge-neutral, spinless, relativistic quantum particles
- The Dirac equationDirac equationThe Dirac equation is a relativistic quantum mechanical wave equation formulated by British physicist Paul Dirac in 1928. It provided a description of elementary spin-½ particles, such as electrons, consistent with both the principles of quantum mechanics and the theory of special relativity, and...
describes the relativistic electron (charged, spin 1/2)
See also
- Particle in a boxParticle in a boxIn quantum mechanics, the particle in a box model describes a particle free to move in a small space surrounded by impenetrable barriers. The model is mainly used as a hypothetical example to illustrate the differences between classical and quantum systems...
- Finite square well
- Delta potential
- Wave packetWave packetIn physics, a wave packet is a short "burst" or "envelope" of wave action that travels as a unit. A wave packet can be analyzed into, or can be synthesized from, an infinite set of component sinusoidal waves of different wavenumbers, with phases and amplitudes such that they interfere...

