In mathematics

Mathematics

Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...

, a partial function from X to Y is a function

Function (mathematics)

In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...

 ƒ: X' → Y, where X' is a subset

Subset

In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...

 of X. It generalizes the concept of a function by not forcing f to map every element of X to an element of Y (only some subset X' of X). If X' = X, then ƒ is called a total function and is equivalent to a function. Partial functions are often used when the exact domain

Domain (mathematics)

In mathematics, the domain of definition or simply the domain of a function is the set of "input" or argument values for which the function is defined...

, X' , is not known (e.g. many functions in computability theory

Computability theory

Computability theory, also called recursion theory, is a branch of mathematical logic that originated in the 1930s with the study of computable functions and Turing degrees. The field has grown to include the study of generalized computability and definability...

).

Specifically, we will say that for any x ∈ X, either:

• ƒ(x) = y ∈ Y (it is defined as a single element in Y) or
• ƒ(x) is undefined.

For example we can consider the square root

Square root

In mathematics, a square root of a number x is a number r such that r2 = x, or, in other words, a number r whose square is x...

 function restricted to the integer

Integer

The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...

s

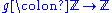
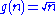
Thus g(n) is only defined for n that are perfect squares

Square number

In mathematics, a square number, sometimes also called a perfect square, is an integer that is the square of an integer; in other words, it is the product of some integer with itself...

 (i.e. 0, 1, 4, 9, 16, ...). So, g(25) = 5, but g(26) is undefined.

Domain of a partial function

There are two distinct meanings in current mathematical usage for the notion of the domain

Domain (mathematics)

In mathematics, the domain of definition or simply the domain of a function is the set of "input" or argument values for which the function is defined...

 of a partial function. Most mathematicians, including recursion theorists

Recursion theory

Computability theory, also called recursion theory, is a branch of mathematical logic that originated in the 1930s with the study of computable functions and Turing degrees. The field has grown to include the study of generalized computability and definability...

, use the term "domain of f" for the set of all values x such that f(x) is defined ( X' above). But some, particularly category theorists

Category theory

Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...

, consider the domain of a partial function f:X→Y to be X, and refer to X' as the domain of definition.

Occasionally, a partial function with domain X and codomain Y is written as f: X ⇸ Y, using an arrow with vertical stroke.

A partial function is said to be injective or surjective when the total function given by the restriction of the partial function to its domain of definition is. A partial function may be both injective and surjective, but the term bijection

Bijection

A bijection is a function giving an exact pairing of the elements of two sets. A bijection from the set X to the set Y has an inverse function from Y to X. If X and Y are finite sets, then the existence of a bijection means they have the same number of elements...

 generally only applies to total functions.

An injective partial function may be inverted

Inverse relation

In mathematics, the inverse relation of a binary relation is the relation that occurs when you switch the order of the elements in the relation. For example, the inverse of the relation 'child of' is the relation 'parent of'...

 to an injective partial function, and a partial function which is both injective and surjective has an injective function as inverse.

Discussion and examples

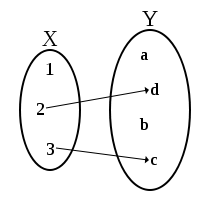
The first diagram above represents a partial function that is not a total function since the element 1 in the left-hand set is not associated with anything in the right-hand set.

Natural logarithm

Consider the natural logarithm

Natural logarithm

The natural logarithm is the logarithm to the base e, where e is an irrational and transcendental constant approximately equal to 2.718281828...

 function mapping the real number

Real number

In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...

s to themselves. The logarithm of a non-positive real is not a real number, so the natural logarithm function doesn't associate any real number in the codomain with any non-positive real number in the domain. Therefore, the natural logarithm function is not a total function when viewed as a function from the reals to themselves, but it is a partial function. If the domain is restricted to only include the positive reals (that is, if the natural logarithm function is viewed as a function from the positive reals to the reals), then the natural logarithm is a total function.

Subtraction of natural numbers

Subtraction of natural numbers (non-negative integers) can be viewed as a partial function: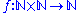


It is only defined when .

Bottom type

In some automated theorem proving

Automated theorem proving

Automated theorem proving or automated deduction, currently the most well-developed subfield of automated reasoning , is the proving of mathematical theorems by a computer program.- Decidability of the problem :...

 systems a partial function is considered as returning the bottom type

Bottom type

In type theory, a theory within mathematical logic, the bottom type is the type that has no values. It is also called the zero or empty type, and is sometimes denoted with falsum .A function whose return type is bottom cannot return any value...

 when it is undefined. The Curry-Howard correspondence uses this to map proofs and computer programs to each other.

In computer science

Computer science

Computer science or computing science is the study of the theoretical foundations of information and computation and of practical techniques for their implementation and application in computer systems...

 a partial function corresponds to a subroutine that raises an exception or loops forever. The IEEE floating point standard defines a Not-a-number value which is returned when a floating point operation is undefined and exceptions are suppressed, e.g. when the square root of a negative number is requested.

In a programming language

Programming language

A programming language is an artificial language designed to communicate instructions to a machine, particularly a computer. Programming languages can be used to create programs that control the behavior of a machine and/or to express algorithms precisely....

 where function parameters are statically typed, a function may be defined as a partial function because the language's type system

Type system

A type system associates a type with each computed value. By examining the flow of these values, a type system attempts to ensure or prove that no type errors can occur...

 cannot express the exact domain of the function, so the programmer instead gives it the smallest domain which is expressible as a type and contains the true domain.

See also

• Bijection
  Bijection
  A bijection is a function giving an exact pairing of the elements of two sets. A bijection from the set X to the set Y has an inverse function from Y to X. If X and Y are finite sets, then the existence of a bijection means they have the same number of elements...
  
  
• Injective function
  Injective function
  In mathematics, an injective function is a function that preserves distinctness: it never maps distinct elements of its domain to the same element of its codomain. In other words, every element of the function's codomain is mapped to by at most one element of its domain...
  
  
• Surjective function
  Surjective function
  In mathematics, a function f from a set X to a set Y is surjective , or a surjection, if every element y in Y has a corresponding element x in X so that f = y...
  
  
• Multivalued function
  Multivalued function
  In mathematics, a multivalued function is a left-total relation; i.e. every input is associated with one or more outputs...
  
  
• Symmetric inverse semigroup
• Densely-defined operator
  Densely-defined operator
  In mathematics — specifically, in operator theory — a densely defined operator is a type of partially defined function; in a topological sense, it is a linear operator that is defined "almost everywhere"...