
Pigeonhole principle
Encyclopedia

Computer science
Computer science or computing science is the study of the theoretical foundations of information and computation and of practical techniques for their implementation and application in computer systems...
, the pigeonhole principle states that if n item
Item
- Organizations :* ITeM, refers to the Uruguay-based Third World Institute , going by its Spanish acronym Instituto del Tercer Mundo* ITEM club, an economic forecasting group based in the United Kingdom- Newspapers :...
s are put into m pigeonholes with n > m, then at least one pigeonhole must contain more than one item. This theorem is exemplified in real-life by truisms like "there must be at least two left gloves or two right gloves in a group of three gloves". It is an example of a counting argument
Combinatorics
Combinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size , deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria ,...
, and despite seeming intuitive it can be used to demonstrate possibly unexpected results; for example, that two people in London have the same number of hairs on their heads (see below).
The first formalization of the idea is believed to have been made by Johann Dirichlet
Johann Peter Gustav Lejeune Dirichlet
Johann Peter Gustav Lejeune Dirichlet was a German mathematician with deep contributions to number theory , as well as to the theory of Fourier series and other topics in mathematical analysis; he is credited with being one of the first mathematicians to give the modern formal definition of a...
in 1834 under the name Schubfachprinzip ("drawer principle" or "shelf principle"). For this reason it is also commonly called Dirichlet's box principle, Dirichlet's drawer principle or simply "Dirichlet principle"—a name that could also refer to the minimum principle for harmonic function
Harmonic function
In mathematics, mathematical physics and the theory of stochastic processes, a harmonic function is a twice continuously differentiable function f : U → R which satisfies Laplace's equation, i.e....
s. The original "drawer" name is still in use in French
French language
French is a Romance language spoken as a first language in France, the Romandy region in Switzerland, Wallonia and Brussels in Belgium, Monaco, the regions of Quebec and Acadia in Canada, and by various communities elsewhere. Second-language speakers of French are distributed throughout many parts...
("principe des tiroirs"), Italian
Italian language
Italian is a Romance language spoken mainly in Europe: Italy, Switzerland, San Marino, Vatican City, by minorities in Malta, Monaco, Croatia, Slovenia, France, Libya, Eritrea, and Somalia, and by immigrant communities in the Americas and Australia...
("principio dei cassetti") and German
German language
German is a West Germanic language, related to and classified alongside English and Dutch. With an estimated 90 – 98 million native speakers, German is one of the world's major languages and is the most widely-spoken first language in the European Union....
("Schubfachprinzip").
Though the most straightforward application is to finite sets (such as pigeons and boxes), it is also used with infinite sets that cannot be put into one-to-one correspondence. To do so requires the formal statement of the pigeonhole principle, which is "there does not exist an injective function
Injective function
In mathematics, an injective function is a function that preserves distinctness: it never maps distinct elements of its domain to the same element of its codomain. In other words, every element of the function's codomain is mapped to by at most one element of its domain...
on finite sets whose codomain
Codomain
In mathematics, the codomain or target set of a function is the set into which all of the output of the function is constrained to fall. It is the set in the notation...
is smaller than its domain
Domain (mathematics)
In mathematics, the domain of definition or simply the domain of a function is the set of "input" or argument values for which the function is defined...
". Advanced mathematical proofs like Siegel's lemma
Siegel's lemma
In transcendental number theory and Diophantine approximation, Siegel's lemma refers to bounds on the solutions of linear equations obtained by the construction of auxiliary functions. The existence of these polynomials was proven by Axel Thue; Thue's proof used Dirichlet's box principle. Carl...
build upon this more general concept.
Softball team
Imagine five people who want to play softballSoftball
Softball is a bat-and-ball sport played between two teams of 10 to 14 players. It is a direct descendant of baseball although there are some key differences: softballs are larger than baseballs, and the pitches are thrown underhand rather than overhand...
items), with a limitation of only four softball teams holes) to choose from. A further limitation is imposed in the form of each of the five refusing to play on a team with any of the other four players. It is impossible to divide five people among four teams without putting two of the people on the same team, and since they refuse to play on the same team, by asserting the pigeonhole principle it is easily deducible that at most four of the five possible players will be able to play.
Sock-picking
Assuming that in a box there are 10 black socks and 12 blue socks, calculate the maximum number of socks needed to be drawn from the box before a pair of the same color can be made. Using the pigeonhole principle, to have at least one pair of the same color holes, one per colour) using one pigeonhole per color, you need only three socks items). In this example, if the first and second sock drawn are not of the same color, the very next sock drawn would complete at least one same-color pair.Hand-shaking
If there are n number of people who can shake hands with one another (where ), the pigeonhole principle shows that there is always a pair of people who will shake hands with the same number of people. As the 'holes', or m, correspond to number of hands shaken, and each person can shake hands with anybody from 0 to other people, this creates possible holes. This is because either the '0' or the hole must be empty (if one person shakes hands with everybody, it's not possible to have another person who shakes hands with nobody; likewise, if one person shakes hands with no one there cannot be a person who shakes hands with everybody). This leaves n people to be placed in at most non-empty holes, guaranteeing duplication.Hair-counting
We can demonstrate there must be at least two people in LondonLondon
London is the capital city of :England and the :United Kingdom, the largest metropolitan area in the United Kingdom, and the largest urban zone in the European Union by most measures. Located on the River Thames, London has been a major settlement for two millennia, its history going back to its...
with the same number of hairs on their heads as follows. A typical human head has around 150,000 hairs; therefore it is reasonable to assume that no one has more than 1,000,000 hairs on their head holes). Since there are more than 1,000,000 people in London (n is bigger than 1 million items), if we assign a pigeonhole to each number of hairs on a person's head, and assign people to pigeonholes according to the number of hairs on each person's head, there must be at least two people with the same number of hair on their heads (or). In the case with the fewest overlaps, there will be at least one person assigned to every pigeonhole, at which point the 1,000,001st person is assigned to the same pigeonhole as someone else. Of course, there may be empty pigeonholes in which case this "collision" happens before we get to the 1,000,000th person. The principle just proves the existence of an overlap; it says nothing of the number of overlaps.
Uses and applications
The pigeonhole principle arises in computer scienceComputer science
Computer science or computing science is the study of the theoretical foundations of information and computation and of practical techniques for their implementation and application in computer systems...
. For example, collisions are inevitable in a hash table
Hash table
In computer science, a hash table or hash map is a data structure that uses a hash function to map identifying values, known as keys , to their associated values . Thus, a hash table implements an associative array...
because the number of possible keys exceeds the number of indices in the array. A hashing algorithm, no matter how clever, cannot avoid these collisions. The principle can also be used to prove that any lossless compression algorithm
Lossless data compression
Lossless data compression is a class of data compression algorithms that allows the exact original data to be reconstructed from the compressed data. The term lossless is in contrast to lossy data compression, which only allows an approximation of the original data to be reconstructed, in exchange...
, provided it makes some inputs smaller (as the name compression suggests), will also make some other inputs larger. Otherwise, the set of all input sequences up to a given length l could be mapped to the (much) smaller set of all sequences of length less than l, and do so without collisions (because the compression is lossless), which possibility the pigeonhole principle excludes.
A notable problem in mathematical analysis
Mathematical analysis
Mathematical analysis, which mathematicians refer to simply as analysis, has its beginnings in the rigorous formulation of infinitesimal calculus. It is a branch of pure mathematics that includes the theories of differentiation, integration and measure, limits, infinite series, and analytic functions...
is, for a fixed irrational number
Irrational number
In mathematics, an irrational number is any real number that cannot be expressed as a ratio a/b, where a and b are integers, with b non-zero, and is therefore not a rational number....
a, to show that the set {[na]: n is an integer} of fractional parts is dense in [0, 1]. After a moment's thought, one finds that it is not easy to explicitly find integers n, m such that , where is a small positive number and a is some arbitrary irrational number. But if one takes M such that , by the pigeonhole principle there must be } such that n1a and n2a are in the same integer subdivision of size 1/M (there are only M such subdivisions between consecutive integers). In particular, we can find n1, n2 such that n1a is in , and n2a is in , for some p, q integers and k in }. We can then easily verify that is in . This implies that , where n = or n = . This shows that 0 is a limit point of {[na]}. We can then use this fact to prove the case for p in
Generalizations of the pigeonhole principle
A generalized version of this principle states that, if n discrete objects are to be allocated to m containers, then at least one container must hold no fewer than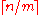 objects, where
objects, where  is the ceiling function, denoting the smallest integer larger than or equal to x. Similarly, at least one container must hold no more than
is the ceiling function, denoting the smallest integer larger than or equal to x. Similarly, at least one container must hold no more than 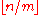 objects, where
objects, where  is the floor function
is the floor functionFloor function
In mathematics and computer science, the floor and ceiling functions map a real number to the largest previous or the smallest following integer, respectively...
, denoting the largest integer smaller than or equal to x.
A probabilistic generalization of the pigeonhole principle states that if n pigeons are randomly put into m pigeonholes with uniform probability 1/m, then at least one pigeonhole will hold more than one pigeon with probability
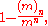
where (m)n is the falling factorial . For n = 0 and for n = 1 (and m > 0), that probability is zero; in other words, if there is just one pigeon, there cannot be a conflict. For n > m (more pigeons than pigeonholes) it is one, in which case it coincides with the ordinary pigeonhole principle. But even if the number of pigeons does not exceed the number of pigeonholes (n ≤ m), due to the random nature of the assignment of pigeons to pigeonholes there is often a substantial chance that clashes will occur. For example, if 2 pigeons are randomly assigned to 4 pigeonholes, there is a 25% chance that at least one pigeonhole will hold more than one pigeon; for 5 pigeons and 10 holes, that probability is 69.76%; and for 10 pigeons and 20 holes it is about 93.45%. If the number of holes stays fixed, there is always a greater probability of a pair when you add more pigeons. This problem is treated at much greater length at birthday paradox
Birthday paradox
In probability theory, the birthday problem or birthday paradox pertains to the probability that, in a set of n randomly chosen people, some pair of them will have the same birthday. By the pigeonhole principle, the probability reaches 100% when the number of people reaches 366. However, 99%...
.
A further probabilistic generalisation is that when a real-valued random variable
Random variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
X has a finite mean
Mean
In statistics, mean has two related meanings:* the arithmetic mean .* the expected value of a random variable, which is also called the population mean....
E(X), then the probability is nonzero that X is greater than or equal to E(X), and similarly the probability is nonzero that X is less than or equal to E(X). To see that this implies the standard pigeonhole principle, take any fixed arrangement of n pigeons into m holes and let X be the number of pigeons in a hole chosen uniformly at random. The mean of X is n/m, so if there are more pigeons than holes the mean is greater than one. Therefore, X is sometimes at least 2.
Infinite sets
The pigeonhole principle can be extended to infinite sets by phrasing it in terms of cardinal numberCardinal number
In mathematics, cardinal numbers, or cardinals for short, are a generalization of the natural numbers used to measure the cardinality of sets. The cardinality of a finite set is a natural number – the number of elements in the set. The transfinite cardinal numbers describe the sizes of infinite...
s: if the cardinality of set A is greater than the cardinality of set B, then there is no injection from A to B. However in this form the principle is tautological
Tautology (logic)
In logic, a tautology is a formula which is true in every possible interpretation. Philosopher Ludwig Wittgenstein first applied the term to redundancies of propositional logic in 1921; it had been used earlier to refer to rhetorical tautologies, and continues to be used in that alternate sense...
, since the meaning of the statement that the cardinality of set A is greater than the cardinality of set B is exactly that there is no injective map from A to B. What makes the situation of finite sets particular is that adding at least one element to a set is sufficient to ensure that the cardinality increases.
See also
- Combinatorial principlesCombinatorial principlesIn proving results in combinatorics several useful combinatorial rules or combinatorial principles are commonly recognized and used.The rule of sum, rule of product, and inclusion-exclusion principle are often used for enumerative purposes. Bijective proofs are utilized to demonstrate that two sets...
- Dedekind-infinite setDedekind-infinite setIn mathematics, a set A is Dedekind-infinite if some proper subset B of A is equinumerous to A. Explicitly, this means that there is a bijective function from A onto some proper subset B of A. A set is Dedekind-finite if it is not Dedekind-infinite.A vaguely related notion is that of a...
- Hilbert's paradox of the Grand HotelHilbert's paradox of the Grand HotelHilbert's paradox of the Grand Hotel is a mathematical veridical paradox about infinite sets presented by German mathematician David Hilbert .-The paradox:...
- Multinomial theoremMultinomial theoremIn mathematics, the multinomial theorem says how to expand a power of a sum in terms of powers of the terms in that sum. It is the generalization of the binomial theorem to polynomials.-Theorem:...
- Ramsey's theoremRamsey's theoremIn combinatorics, Ramsey's theorem states that in any colouring of the edges of a sufficiently large complete graph, one will find monochromatic complete subgraphs...
- Combinatorial proofCombinatorial proofIn mathematics, the term combinatorial proof is often used to mean either of two types of proof of an identity in enumerative combinatorics that either states that two sets of combinatorial configurations, depending on one or more parameters, have the same number of elements , or gives a formula...
External links
- "The strange case of The Pigeon-hole Principle"; Edsger DijkstraEdsger DijkstraEdsger Wybe Dijkstra ; ) was a Dutch computer scientist. He received the 1972 Turing Award for fundamental contributions to developing programming languages, and was the Schlumberger Centennial Chair of Computer Sciences at The University of Texas at Austin from 1984 until 2000.Shortly before his...
investigates interpretations and reformulations of the principle. - "The Pigeon Hole Principle"; Elementary examples of the principle in use by Larry Cusick.
- "Pigeonhole Principle from Interactive Mathematics Miscellany and Puzzles"; basic Pigeonhole Principle analysis and examples by Alexander Bogomolny.
- "The Puzzlers' Pigeonhole"; Alexander Bogomolny on the importance of the principle in the field of puzzle solving and analysis.

