Hyperbolic quaternion multiplication

×	1	i	j	k
1	1	i	j	k
i	i	+1	k	−j
j	j	−k	+1	i
k	k	j	−i	+1

In the abstract algebra

Abstract algebra

Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...

 of algebras over a field

Algebra over a field

In mathematics, an algebra over a field is a vector space equipped with a bilinear vector product. That is to say, it isan algebraic structure consisting of a vector space together with an operation, usually called multiplication, that combines any two vectors to form a third vector; to qualify as...

, the hyperbolic quaternion
is a mutated quaternion

Quaternion

In mathematics, the quaternions are a number system that extends the complex numbers. They were first described by Irish mathematician Sir William Rowan Hamilton in 1843 and applied to mechanics in three-dimensional space...

 where 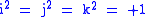instead of the usual −1.

The four-dimensional algebra of hyperbolic quaternions incorporates some of the features of the older and larger algebra of biquaternions. They both contain subalgebras isomorphic to the split complex number plane. Furthermore, just as the quaternion algebra H can be viewed as a union of complex planes, so the hyperbolic quaternion algebra is a union of split-complex number planes sharing the same real line

Real line

In mathematics, the real line, or real number line is the line whose points are the real numbers. That is, the real line is the set of all real numbers, viewed as a geometric space, namely the Euclidean space of dimension one...

.

It was Alexander Macfarlane

Alexander Macfarlane

Alexander Macfarlane was a Nova Scotia lawyer and political figure. He was a member of the Canadian Senate from 1870 to 1898. His surname also appears as McFarlane in some sources....

 who promoted this concept in the 1890s as his Algebra of Physics, first through the American Association for the Advancement of Science

American Association for the Advancement of Science

The American Association for the Advancement of Science is an international non-profit organization with the stated goals of promoting cooperation among scientists, defending scientific freedom, encouraging scientific responsibility, and supporting scientific education and science outreach for the...

 in 1891, then through his 1894 book of five Papers in Space Analysis, and in a series of lectures at Lehigh University

Lehigh University

Lehigh University is a private, co-educational university located in Bethlehem, Pennsylvania, in the Lehigh Valley region of the United States. It was established in 1865 by Asa Packer as a four-year technical school, but has grown to include studies in a wide variety of disciplines...

 in 1900 (see Historical Review below).

The hyperbolic quaternions form a non-associative ring; the failure of associativity

Associativity

In mathematics, associativity is a property of some binary operations. It means that, within an expression containing two or more occurrences in a row of the same associative operator, the order in which the operations are performed does not matter as long as the sequence of the operands is not...

 in this algebra curtails the facility of this algebra in transformation theory. Nevertheless,
this algebra put a focus on analytical kinematics by suggesting a mathematical model

Mathematical model

A mathematical model is a description of a system using mathematical concepts and language. The process of developing a mathematical model is termed mathematical modeling. Mathematical models are used not only in the natural sciences and engineering disciplines A mathematical model is a...

:
When one selects a unit vector r in the hyperbolic quaternions, then r ² = +1. The plane 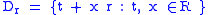with hyperbolic quaternion multiplication is a commutative and associative subalgebra isomorphic to the split-complex number plane.
The hyperbolic versor 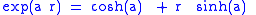 transforms D_r by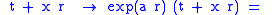
Since the direction r in space is arbitrary, this hyperbolic quaternion multiplication can express any Lorentz boost using the parameter a called rapidity

Rapidity

In relativity, rapidity is an alternative to speed as a framework for measuring motion. On parallel velocities rapidities are simply additive, unlike speeds at relativistic velocities. For low speeds, rapidity and speed are proportional, but for high speeds, rapidity takes a larger value. The...

. However, the hyperbolic quaternion algebra is deficient for representing the full Lorentz group

Lorentz group

In physics , the Lorentz group is the group of all Lorentz transformations of Minkowski spacetime, the classical setting for all physical phenomena...

 (see biquaternion instead).

Writing in 1967 about the dialogue on vector methods in the 1890s, a historian commented

The introduction of another system of vector analysis, even a sort of compromise system such as Macfarlane's, could scarcely be well received by the advocates of the already existing systems and moreover probably acted to broaden the question beyond the comprehension of the as-yet uninitiated reader.

Algebraic structure

Like the quaternions, the set of hyperbolic quaternions form a vector space

Vector space

A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...

 over the real numbers of dimension

Dimension

In physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...

 4. A linear combination

Linear combination

In mathematics, a linear combination is an expression constructed from a set of terms by multiplying each term by a constant and adding the results...

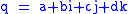
is a hyperbolic quaternion when 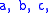and are real numbers and the basis set 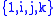has these products:


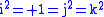
Unlike the ordinary quaternions, the hyperbolic quaternions are not associative. For example, , while 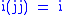. The first three relations show that products of the (non-real) basis elements are anti-commutative. Although this basis set does not form a group

Group (mathematics)

In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...

, the set


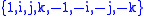
forms a quasigroup

Quasigroup

In mathematics, especially in abstract algebra, a quasigroup is an algebraic structure resembling a group in the sense that "division" is always possible...

. One also notes that any subplane of the set M of hyperbolic quaternions that contains the real axis forms a plane of split-complex number

Split-complex number

In abstract algebra, the split-complex numbers are a two-dimensional commutative algebra over the real numbers different from the complex numbers. Every split-complex number has the formwhere x and y are real numbers...

s. If


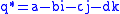
is the conjugate of , then the product


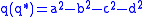
is the quadratic form

Quadratic form

In mathematics, a quadratic form is a homogeneous polynomial of degree two in a number of variables. For example,4x^2 + 2xy - 3y^2\,\!is a quadratic form in the variables x and y....

 used in spacetime theory.
In fact, the bilinear form called the Minkowski inner product arises as the negative of the real part of the hyperbolic quaternion product pq* :.
Note that the set of units

Unit (ring theory)

In mathematics, an invertible element or a unit in a ring R refers to any element u that has an inverse element in the multiplicative monoid of R, i.e. such element v that...

 U = {q : qq* ≠ 0 } is not closed under multiplication. See the references (external link) for details.

Geometry

Later, Macfarlane published an article in the Proceedings of the Royal Society at Edinburgh in 1900. In it he treats a model for hyperbolic space

Hyperbolic space

In mathematics, hyperbolic space is a type of non-Euclidean geometry. Whereas spherical geometry has a constant positive curvature, hyperbolic geometry has a negative curvature: every point in hyperbolic space is a saddle point...

 H³ on the hyperboloid
.

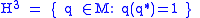This isotropic model is called the hyperboloid model

Hyperboloid model

In geometry, the hyperboloid model, also known as the Minkowski model or the Lorentz model , is a model of n-dimensional hyperbolic geometry in which points are represented by the points on the forward sheet S+ of a two-sheeted hyperboloid in -dimensional Minkowski space and m-planes are...

 and consists of all the hyperbolic versors in the ring of hyperbolic quaternions.

Historical review

The 1890s felt the influence of the posthumous publications of W. K. Clifford

W. K. Clifford

W. K. Clifford may refer to:*William Kingdon Clifford, British mathematician and philosopher*Lucy Clifford Mrs W. K. Clifford, wife of the above, British novelist and journalist...

 and the continuous groups of Sophus Lie

Sophus Lie

Marius Sophus Lie was a Norwegian mathematician. He largely created the theory of continuous symmetry, and applied it to the study of geometry and differential equations.- Biography :...

. An example of a one-parameter group

One-parameter group

In mathematics, a one-parameter group or one-parameter subgroup usually means a continuous group homomorphismfrom the real line R to some other topological group G...

 is the hyperbolic versor with the hyperbolic angle

Hyperbolic angle

In mathematics, a hyperbolic angle is a geometric figure that divides a hyperbola. The science of hyperbolic angle parallels the relation of an ordinary angle to a circle...

 parameter. This parameter is part of the polar decomposition of a split-complex number. But it is a startling aspect of finite mathematics that makes the hyperbolic quaternion ring different:

The basis 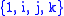of the vector space of hyperbolic quaternions is not closed

Closure (mathematics)

In mathematics, a set is said to be closed under some operation if performance of that operation on members of the set always produces a unique member of the same set. For example, the real numbers are closed under subtraction, but the natural numbers are not: 3 and 8 are both natural numbers, but...

 under multiplication: for example, 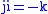. Nevertheless, the set 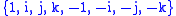is closed under multiplication. It satisfies all the properties of an abstract group except the associativity property; being finite, it is a latin square

Latin square

In combinatorics and in experimental design, a Latin square is an n × n array filled with n different symbols, each occurring exactly once in each row and exactly once in each column...

 or quasigroup

Quasigroup

In mathematics, especially in abstract algebra, a quasigroup is an algebraic structure resembling a group in the sense that "division" is always possible...

, a peripheral mathematical structure

Mathematical structure

In mathematics, a structure on a set, or more generally a type, consists of additional mathematical objects that in some manner attach to the set, making it easier to visualize or work with, or endowing the collection with meaning or significance....

. Loss of the associativity property of multiplication as found in quasigroup theory is not consistent with linear algebra

Linear algebra

Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...

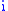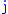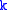 since all linear transformations compose in an associative manner. Yet physical scientists were calling in the 1890s for mutation of the squares of ,, and to be 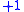instead of :
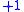The Yale University

Yale University

Yale University is a private, Ivy League university located in New Haven, Connecticut, United States. Founded in 1701 in the Colony of Connecticut, the university is the third-oldest institution of higher education in the United States...

 physicist Willard Gibbs had pamphlets with the plus one square in his three-dimensional vector system. Oliver Heaviside

Oliver Heaviside

Oliver Heaviside was a self-taught English electrical engineer, mathematician, and physicist who adapted complex numbers to the study of electrical circuits, invented mathematical techniques to the solution of differential equations , reformulated Maxwell's field equations in terms of electric and...

 in England wrote columns in the Electrician, a trade paper, advocating the positive square. In 1892 he brought his work together in Transactions of the Royal Society A where he says his vector system is

simply the elements of Quaternions without quaternions, with the notation simplified to the uttermost, and with the very inconvenient minus sign before scalar product done away with.

So the appearance of Macfarlane's hyperbolic quaternions had some motivation, but the disagreeable non-associativity precipitated a reaction. Cargill Gilston Knott

Cargill Gilston Knott

Cargill Gilston Knott was a Scottish physicist and mathematician who was a pioneer in seismological research. He spent his early career in Japan...

 was moved to offer the following:

Theorem (Knott 1893)

If a 4-algebra on basis 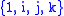is associative and off-diagonal products are given by Hamilton's rules, then .

Proof: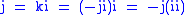, so . Cycle the letters 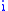, , 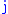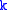to obtain 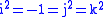. QED.

This theorem needed statement to justify resistance to the call of the physicists and the Electrician. The quasigroup stimulated a considerable stir in the 1890s: the journal Nature

Nature (journal)

Nature, first published on 4 November 1869, is ranked the world's most cited interdisciplinary scientific journal by the Science Edition of the 2010 Journal Citation Reports...

was especially conducive to an exhibit of what was known by giving two digests of Knott's work as well as those of several other vector theorists. Michael J. Crowe devotes chapter six of his book A History of Vector Analysis

A History of Vector Analysis

A History of Vector Analysis is a book on the history of vector analysis by Michael J. Crowe, originally published by the University of Notre Dame Press....

to the various published views, and notes the hyperbolic quaternion:

Macfarlane constructed a new system of vector analysis more in harmony with Gibbs-Heaviside system than with the quaternion system. ...he...defined a full product of two vectors which was comparable to the full quaternion product except that the scalar part was positive, not negative as in the older system.

In 1899 Charles Jasper Joly

Charles Jasper Joly

Charles Jasper Joly was an Irish mathematician and astronomer who became Royal Astronomer of Ireland.-Life:...

 noted the hyperbolic quaternion and the non-associativity property while ascribing its origin to Oliver Heaviside.

The hyperbolic quaternions, as the Algebra of Physics, undercut the claim that ordinary quaternions made on physics. As for mathematics, the hyperbolic quaternion is another hypercomplex number

Hypercomplex number

In mathematics, a hypercomplex number is a traditional term for an element of an algebra over a field where the field is the real numbers or the complex numbers. In the nineteenth century number systems called quaternions, tessarines, coquaternions, biquaternions, and octonions became established...

, as such structures were called at the time. By the 1890s Richard Dedekind

Richard Dedekind

Julius Wilhelm Richard Dedekind was a German mathematician who did important work in abstract algebra , algebraic number theory and the foundations of the real numbers.-Life:...

 had introduced the ring

Ring (mathematics)

In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...

 concept into commutative algebra, and the vector space

Vector space

A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...

 concept was being abstracted by Peano. In 1899 Alfred North Whitehead

Alfred North Whitehead

Alfred North Whitehead, OM FRS was an English mathematician who became a philosopher. He wrote on algebra, logic, foundations of mathematics, philosophy of science, physics, metaphysics, and education...

 promoted Universal algebra

Universal algebra

Universal algebra is the field of mathematics that studies algebraic structures themselves, not examples of algebraic structures....

, advocating for inclusivity. The concepts of quasigroup and algebra over a field

Algebra over a field

In mathematics, an algebra over a field is a vector space equipped with a bilinear vector product. That is to say, it isan algebraic structure consisting of a vector space together with an operation, usually called multiplication, that combines any two vectors to form a third vector; to qualify as...

 are examples of mathematical structure

Mathematical structure

In mathematics, a structure on a set, or more generally a type, consists of additional mathematical objects that in some manner attach to the set, making it easier to visualize or work with, or endowing the collection with meaning or significance....

s describing hyperbolic quaternions. More generally, abstract algebra

Abstract algebra

Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...

 developed in the twentieth century with the sorting of mathematical structures as well as delving into their contents. Referring to the abstract structures as categories

Category (mathematics)

In mathematics, a category is an algebraic structure that comprises "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose...

, the science of category theory

Category theory

Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...

 describes the system of structures.

MacFarlane's hyperbolic quaternion paper of 1900

The Proceedings of the Royal Society at Edinburgh published "Hyperbolic Quaternions"
in 1900, a paper in which Macfarlane regains associativity for multiplication by reverting
to complexified quaternions. While there he used some expressions later
made famous by Wolfgang Pauli

Wolfgang Pauli

Wolfgang Ernst Pauli was an Austrian theoretical physicist and one of the pioneers of quantum physics. In 1945, after being nominated by Albert Einstein, he received the Nobel Prize in Physics for his "decisive contribution through his discovery of a new law of Nature, the exclusion principle or...

: where Macfarlane wrote,
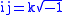
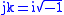
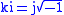the Pauli matrices

Pauli matrices

The Pauli matrices are a set of three 2 × 2 complex matrices which are Hermitian and unitary. Usually indicated by the Greek letter "sigma" , they are occasionally denoted with a "tau" when used in connection with isospin symmetries...

 satisfy
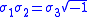
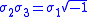
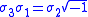
while referring to the same complexified quaternions.

The opening sentence of the paper is "It is well known that quaternions are intimately connected with spherical trigonometry

Spherical trigonometry

Spherical trigonometry is a branch of spherical geometry which deals with polygons on the sphere and the relationships between the sides and the angles...

 and in fact they reduce the subject to a branch of algebra." This statement may be verified by reference to the contemporary work Vector Analysis which works with a reduced quaternion system based on dot product

Dot product

In mathematics, the dot product or scalar product is an algebraic operation that takes two equal-length sequences of numbers and returns a single number obtained by multiplying corresponding entries and then summing those products...

 and cross product

Cross product

In mathematics, the cross product, vector product, or Gibbs vector product is a binary operation on two vectors in three-dimensional space. It results in a vector which is perpendicular to both of the vectors being multiplied and normal to the plane containing them...

. In Macfarlane's paper there is an effort to produce "trigonometry on the surface of the equilateral hyperboloids" through the algebra of hyperbolic quaternions, now re-identified in an associative ring of eight real dimensions. The effort is reinforced by a plate of nine figures on page 181. They illustrate the descriptive power of his "space analysis" method. For example, figure 7 is the
common Minkowski diagram

Minkowski diagram

The Minkowski diagram was developed in 1908 by Hermann Minkowski and provides an illustration of the properties of space and time in the special theory of relativity. It allows a quantitative understanding of the corresponding phenomena like time dilation and length contraction without mathematical...

 used today in special relativity

Special relativity

Special relativity is the physical theory of measurement in an inertial frame of reference proposed in 1905 by Albert Einstein in the paper "On the Electrodynamics of Moving Bodies".It generalizes Galileo's...

 to discuss change of velocity of a frame of reference and relativity of simultaneity

Relativity of simultaneity

In physics, the relativity of simultaneity is the concept that simultaneity–whether two events occur at the same time–is not absolute, but depends on the observer's reference frame. According to the special theory of relativity, it is impossible to say in an absolute sense whether two events occur...

.

On page 173 Macfarlane expands on his greater theory of quaternion variables. By way of contrast he notes that Felix Klein

Felix Klein

Christian Felix Klein was a German mathematician, known for his work in group theory, function theory, non-Euclidean geometry, and on the connections between geometry and group theory...

 appears not to look beyond the theory of Quaternions and spatial rotation

Quaternions and spatial rotation

Unit quaternions provide a convenient mathematical notation for representing orientations and rotations of objects in three dimensions. Compared to Euler angles they are simpler to compose and avoid the problem of gimbal lock. Compared to rotation matrices they are more numerically stable and may...

.