In geometry, the Poincaré disk model, also called the conformal disk model, is a model of n-dimensional hyperbolic geometry

Hyperbolic geometry

In mathematics, hyperbolic geometry is a non-Euclidean geometry, meaning that the parallel postulate of Euclidean geometry is replaced...

 in which the points of the geometry are in an n-dimensional disk, or unit ball

Ball (mathematics)

In mathematics, a ball is the space inside a sphere. It may be a closed ball or an open ball ....

, and the straight lines of the hyperbolic geometry are segments of circles contained in the disk orthogonal to the boundary of the disk, or else diameters of the disk. Along with the Klein model

Klein model

In geometry, the Beltrami–Klein model, also called the projective model, Klein disk model, and the Cayley–Klein model, is a model of n-dimensional hyperbolic geometry in which points are represented by the points in the interior of the n-dimensional unit ball and lines are represented by the...

 and the Poincaré half-space model, it was proposed by Eugenio Beltrami

Eugenio Beltrami

Eugenio Beltrami was an Italian mathematician notable for his work concerning differential geometry and mathematical physics...

 who used these models to show hyperbolic geometry was equiconsistent

Equiconsistency

In mathematical logic, two theories are equiconsistent if, roughly speaking, they are "as consistent as each other".It is not in general possible to prove the absolute consistency of a theory T...

 with Euclidean geometry.

Metric

If u and v are two vectors in real n-dimensional vector space Rⁿ with the usual Euclidean norm, both of which have norm less than 1, then we may define an isometric invariant

Isometry

In mathematics, an isometry is a distance-preserving map between metric spaces. Geometric figures which can be related by an isometry are called congruent.Isometries are often used in constructions where one space is embedded in another space...

 by


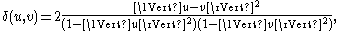
where 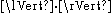denotes the usual Euclidean norm. Then the distance function is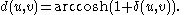


Such a distance function is defined for any two vectors of norm less than one, and makes the set of such vectors into a metric space which is a model of hyperbolic space of constant curvature −1. The model has the conformal property that the angle between two intersecting curves in hyperbolic space is the same as the angle in the model.

The associated metric tensor

Metric tensor

In the mathematical field of differential geometry, a metric tensor is a type of function defined on a manifold which takes as input a pair of tangent vectors v and w and produces a real number g in a way that generalizes many of the familiar properties of the dot product of vectors in Euclidean...

 of the Poincaré disk model is given by


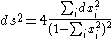
where the x_i are the Cartesian coordinates of the ambient Euclidean space. The geodesic

Geodesic

In mathematics, a geodesic is a generalization of the notion of a "straight line" to "curved spaces". In the presence of a Riemannian metric, geodesics are defined to be the shortest path between points in the space...

s of the disk model are circles perpendicular to the boundary sphere Sⁿ⁻¹.

Relation to the hyperboloid model

The Poincaré disk model, as well as the Klein model

Klein model

In geometry, the Beltrami–Klein model, also called the projective model, Klein disk model, and the Cayley–Klein model, is a model of n-dimensional hyperbolic geometry in which points are represented by the points in the interior of the n-dimensional unit ball and lines are represented by the...

, are related to the hyperboloid model

Hyperboloid model

In geometry, the hyperboloid model, also known as the Minkowski model or the Lorentz model , is a model of n-dimensional hyperbolic geometry in which points are represented by the points on the forward sheet S+ of a two-sheeted hyperboloid in -dimensional Minkowski space and m-planes are...

 projectively. If we have a point [t, x₁, ..., x_n] on the upper sheet of the hyperboloid of the hyperboloid model, thereby defining a point in the hyperboloid model, we may project it onto the hypersurface t = 0 by intersecting it with a line drawn through [−1, 0, ..., 0]. The result is the corresponding point of the Poincaré disk model.

For Cartesian coordinates (t, x_i) on the hyperboloid and (y_i) on the plane, the conversion formulae are:



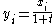
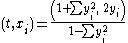
Compare the formulae for stereographic projection

Stereographic projection

The stereographic projection, in geometry, is a particular mapping that projects a sphere onto a plane. The projection is defined on the entire sphere, except at one point — the projection point. Where it is defined, the mapping is smooth and bijective. It is conformal, meaning that it...

 between a sphere and a plane.

Analytic geometry constructions in the hyperbolic plane

A basic construction of analytic geometry

Analytic geometry

Analytic geometry, or analytical geometry has two different meanings in mathematics. The modern and advanced meaning refers to the geometry of analytic varieties...

 is to find a line through two given points. In the Poincaré disk model, lines in the plane are defined by portions of circles having equations of the form


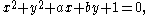
which is the general form of a circle orthogonal to the unit circle, or else by diameters. Given two points u and v in the disk which do not lie on a diameter, we can solve for the circle of this form passing through both points, and obtain


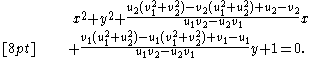
If the points u and v are points on the boundary of the disk not lying at the endpoints of a diameter, the above simplifies to

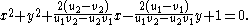
Angles

We may compute the angle between the circular arc whose endpoints (ideal points) are given by unit vectors u and v, and the arc whose endpoints are s and t, by means of a formula. Since the ideal points are the same in the Klein model and the Poincaré disk model, the formulas are identical for each model.

If both models' lines are diameters, so that v = −u and t = −s, then we are merely finding the angle between two unit vectors, and the formula for the angle θ is


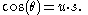
If v = −u but not t = −s, the formula becomes, in terms of the wedge product,


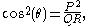
where




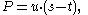
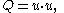
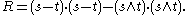
If both chords are not diameters, the general formula obtains


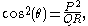
where




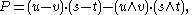
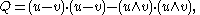
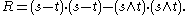
Using the Binet–Cauchy identity and the fact that these are unit vectors we may rewrite the above expressions purely in terms of the dot product

Dot product

In mathematics, the dot product or scalar product is an algebraic operation that takes two equal-length sequences of numbers and returns a single number obtained by multiplying corresponding entries and then summing those products...

, as

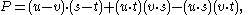
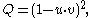
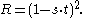
Artistic realizations

The M.C. Escher

M. C. Escher

Maurits Cornelis Escher , usually referred to as M. C. Escher , was a Dutch graphic artist. He is known for his often mathematically inspired woodcuts, lithographs, and mezzotints...

 print Circle Limit IV is an artistic visualization of the Poincaré disk.

See also

• Hyperbolic geometry
  Hyperbolic geometry
  In mathematics, hyperbolic geometry is a non-Euclidean geometry, meaning that the parallel postulate of Euclidean geometry is replaced...
  
  
• Klein model
  Klein model
  In geometry, the Beltrami–Klein model, also called the projective model, Klein disk model, and the Cayley–Klein model, is a model of n-dimensional hyperbolic geometry in which points are represented by the points in the interior of the n-dimensional unit ball and lines are represented by the...
  
  
• Poincaré half-plane model
  Poincaré half-plane model
  In non-Euclidean geometry, the Poincaré half-plane model is the upper half-plane , together with a metric, the Poincaré metric, that makes it a model of two-dimensional hyperbolic geometry....
  
  
• Poincaré metric
  Poincaré metric
  In mathematics, the Poincaré metric, named after Henri Poincaré, is the metric tensor describing a two-dimensional surface of constant negative curvature. It is the natural metric commonly used in a variety of calculations in hyperbolic geometry or Riemann surfaces.There are three equivalent...
  
  
• Pseudosphere
  Pseudosphere
  In geometry, the term pseudosphere is used to describe various surfaces with constant negative gaussian curvature. Depending on context, it can refer to either a theoretical surface of constant negative curvature, to a tractricoid, or to a hyperboloid....
  
  
• Hyperboloid model
  Hyperboloid model
  In geometry, the hyperboloid model, also known as the Minkowski model or the Lorentz model , is a model of n-dimensional hyperbolic geometry in which points are represented by the points on the forward sheet S+ of a two-sheeted hyperboloid in -dimensional Minkowski space and m-planes are...
  
  
• Inversive geometry
• Uniform tilings in hyperbolic plane
  Uniform tilings in hyperbolic plane
  There are an infinite number of uniform tilings on the hyperbolic plane based on the where 1/p + 1/q + 1/r ...