
Cauchy-Riemann equations
Encyclopedia
In mathematics
, the Cauchy–Riemann differential equations in complex analysis
, named after Augustin Cauchy
and Bernhard Riemann
, consist of a system of two partial differential equation
s which must be satisfied if we know that a complex function is complex differentiable. Moreover, the equations are necessary and sufficient conditions for complex differentiation once we assume that its real and imaginary parts are differentiable real functions of two variables. This system of equations first appeared in the work of Jean le Rond d'Alembert
. Later, Leonhard Euler
connected this system to the analytic functions . then used these equations to construct his theory of functions. Riemann's dissertation on the theory of functions appeared in 1851.
The Cauchy–Riemann equations on a pair of real-valued functions of two real variables u(x,y) and v(x,y) are the two equations:
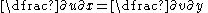
and
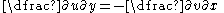
Typically u and v are taken to be the real and imaginary parts respectively of a complex
-valued function of a single complex variable z=x+iy, f(x + iy) = u(x,y) + iv(x,y). Suppose that u and v are real-differentiable at a point in an open subset of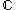 , which can be considered as functions from
, which can be considered as functions from 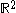 to
to 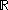 . This implies that the partial derivatives of u and v exist (although they need not be continuous) and we can approximate small variations of f linearly. Then f = u + iv is complex-differentiable at that point if and only if the partial derivatives of u and v satisfy the Cauchy–Riemann equations (1a) and (1b) at that point. The sole existence of partial derivatives satisfying the Cauchy-Riemann equations is not enough to ensure complex differentiability at that point. It is necessary to make sure that u and v are real differentiable, which is a stronger condition than the existence of the partial derivatives but it is not necessary to require continuity of these partial derivatives.
. This implies that the partial derivatives of u and v exist (although they need not be continuous) and we can approximate small variations of f linearly. Then f = u + iv is complex-differentiable at that point if and only if the partial derivatives of u and v satisfy the Cauchy–Riemann equations (1a) and (1b) at that point. The sole existence of partial derivatives satisfying the Cauchy-Riemann equations is not enough to ensure complex differentiability at that point. It is necessary to make sure that u and v are real differentiable, which is a stronger condition than the existence of the partial derivatives but it is not necessary to require continuity of these partial derivatives.
Holomorphy is the property of a complex function of being differentiable at every point of an open and connected subset of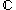 (this is called a domain in
(this is called a domain in 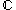 ). Consequently, we can assert that a complex function f, whose real and imaginary parts u and v are real-differentiable functions, is holomorphic if and only if, equations (1a) and (1b) are satisfied throughout the domain we are dealing with.
). Consequently, we can assert that a complex function f, whose real and imaginary parts u and v are real-differentiable functions, is holomorphic if and only if, equations (1a) and (1b) are satisfied throughout the domain we are dealing with.
The reason why Euler and some other authors relate the Cauchy-Riemann equations with analyticity
is that a major theorem in complex analysis
says that holomorphic functions are analytic
and viceversa. This means that, in complex analysis, a function that is complex-differentiable in a whole domain (holomorphic) is the same as an analytic function. This is not true for real differentiable functions.
: in other words they encapsulate the notion of function of a complex variable by means of conventional differential calculus
. In the theory there are several other major ways of looking at this notion, and the translation of the condition into other language is often needed.
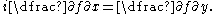
In this form, the equations correspond structurally to the condition that the Jacobian matrix is of the form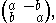
where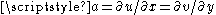 and
and 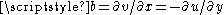 . A matrix of this form is the matrix representation of a complex number. Geometrically, such a matrix is always the composition
. A matrix of this form is the matrix representation of a complex number. Geometrically, such a matrix is always the composition
of a rotation
with a scaling, and in particular preserves angle
s. Consequently, a function satisfying the Cauchy–Riemann equations, with a nonzero derivative, preserves the angle between curves in the plane. That is, the Cauchy–Riemann equations are the conditions for a function to be conformal
.
f(z) = u(z) + i v(z)
is a function of a complex number z. Then the complex derivative of ƒ at a point zis defined by
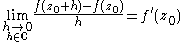
provided this limit exists.
If this limit exists, then it may be computed by taking the limit as h → 0 along the real axis or imaginary axis; in either case it should give the same result. Approaching along the real axis, one finds

On the other hand, approaching along the imaginary axis,
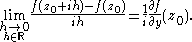
The equality of the derivative of ƒ taken along the two axes is
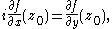
which are the Cauchy–Riemann equations (2) at the point z0.
Conversely, if ƒ : C → C is a function which is differentiable when regarded as a function on R2, then ƒ is complex differentiable if and only if the Cauchy–Riemann equations hold. In other words, if u and v are real-differentiable functions of two real variables, obviously u+iv is a (complex-valued) real-differentiable function, but u+iv is complex-differentiable if and only if the Cauchy-Riemann equations hold.
Indeed, following , suppose ƒ is a complex function defined in an open set Ω ⊂ C. Then, writing z = x + i y for every z ∈ Ω, one can also regard Ω as an open subset of R2, and ƒ as a function of two real variables x and y, which maps Ω ⊂ R2 to C. We consider the Cauchy–Riemann equations at z = 0 assuming ƒ(z) = 0, just for notational simplicity – the proof is identical in general case. So assume ƒ is differentiable at 0, as a function of two real variables from Ω to C. This is equivalent to the existence of two complex numbers and
and 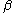 (which are the partial derivatives of ƒ) such that
(which are the partial derivatives of ƒ) such that
where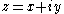 and
and 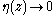 as
as 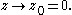 Since
Since  and
and 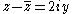 , the above can be re-written as
, the above can be re-written as
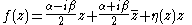
Defining the two Wirtinger derivatives
as
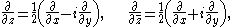
the above equality can be written as
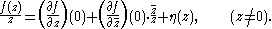
For real values of , we have
, we have 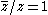 and for purely imaginary
and for purely imaginary  we have
we have 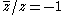 hence
hence 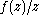 has a limit at 0 (i.e., ƒ is complex differentiable at 0) if and only if
has a limit at 0 (i.e., ƒ is complex differentiable at 0) if and only if 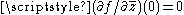 . But this is exactly the Cauchy–Riemann equations, thus ƒ is differentiable at 0 if and only if the Cauchy–Riemann equations hold at 0.
. But this is exactly the Cauchy–Riemann equations, thus ƒ is differentiable at 0 if and only if the Cauchy–Riemann equations hold at 0.
of z, denoted , is defined by
, is defined by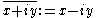
for real x and y. The Cauchy–Riemann equations can then be written as a single equation
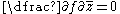
by using the Wirtinger derivative respect to the conjugate variable
. In this form, the Cauchy–Riemann equations can be interpreted as the statement that f is independent of the variable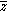 . As such, we can view analytic functions as true functions of one complex variable as opposed to complex functions of two real variables.
. As such, we can view analytic functions as true functions of one complex variable as opposed to complex functions of two real variables.
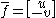
regarded as a (real) two-component vector. Then the second Cauchy–Riemann equation (1b) asserts that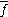 is irrotational
is irrotational
:

The first Cauchy–Riemann equation (1a) asserts that the vector field is solenoidal (or divergence
-free):
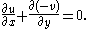
Owing respectively to Green's theorem
and the divergence theorem
, such a field is necessarily conserved and free from sources or sinks, having net flux equal to zero through any open domain. (These two observations combine as real and imaginary parts in Cauchy's integral theorem
.) In fluid dynamics
, such a vector field is a potential flow
. In magnetostatics
, such vector fields model static magnetic field
s on a region of the plane containing no current. In electrostatics
, they model static electric fields in a region of the plane containing no electric charge.
s. If (1a) and (1b) hold for a differentiable pair of functions u and v, then so do
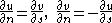
for any coordinate system such that the pair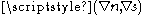 is orthonormal and positively oriented
is orthonormal and positively oriented
. As a consequence, in particular, in the system of coordinates given by the polar representation , the equations then take the form
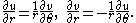
Combining these into one equation for ƒ gives
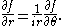
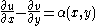
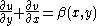
for some given functions α(x,y) and β(x,y) defined in an open subset of R2. These equations are usually combined into a single equation
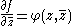
where f = u + iv and φ = (α + iβ)/2.
If φ is Ck, then the inhomogeneous equation is explicitly solvable in any bounded domain D, provided φ is continuous on the closure
of D. Indeed, by the Cauchy integral formula,
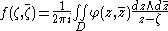
for all ζ ∈ D.
as a function . Then Goursat's theorem asserts that ƒ is analytic in an open complex domain Ω if and only if it satisfies the Cauchy–Riemann equation in the domain . In particular, continuous differentiability of ƒ need not be assumed .
The hypotheses of Goursat's theorem can be weakened significantly. If is continuous in an open set Ω and the partial derivative
s of ƒ with respect to x and y exist in Ω, and satisfies the Cauchy–Riemann equations throughout Ω, then ƒ is holomorphic (and thus analytic). This result is the Looman–Menchoff theorem
.
The hypothesis that ƒ obey the Cauchy–Riemann equations throughout the domain Ω is essential. It is possible to construct a continuous function satisfying the Cauchy–Riemann equations at a point, but which is not analytic at the point (e.g., ƒ(z) = . Similarly, some additional assumption is needed besides the Cauchy–Riemann equations (such as continuity), as the following example illustrates
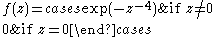
which satisfies the Cauchy–Riemann equations everywhere, but fails to be continuous at z = 0.
Nevertheless, if a function satisfies the Cauchy–Riemann equations in an open set in a weak sense
, then the function is analytic. More precisely :
This is in fact a special case of a more general result on the regularity of solutions of hypoelliptic partial differential equations.
. They form a significant overdetermined system
of PDEs. As often formulated, the d-bar operator
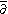
annihilates holomorphic functions. This generalizes most directly the formulation
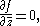
where

. More complicated, generally non-linear Bäcklund transforms, such as in the sine-Gordon equation
, are of great interest in the theory of soliton
s and integrable system
s.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the Cauchy–Riemann differential equations in complex analysis
Complex analysis
Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is useful in many branches of mathematics, including number theory and applied mathematics; as well as in physics,...
, named after Augustin Cauchy
Augustin Louis Cauchy
Baron Augustin-Louis Cauchy was a French mathematician who was an early pioneer of analysis. He started the project of formulating and proving the theorems of infinitesimal calculus in a rigorous manner, rejecting the heuristic principle of the generality of algebra exploited by earlier authors...
and Bernhard Riemann
Bernhard Riemann
Georg Friedrich Bernhard Riemann was an influential German mathematician who made lasting contributions to analysis and differential geometry, some of them enabling the later development of general relativity....
, consist of a system of two partial differential equation
Partial differential equation
In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
s which must be satisfied if we know that a complex function is complex differentiable. Moreover, the equations are necessary and sufficient conditions for complex differentiation once we assume that its real and imaginary parts are differentiable real functions of two variables. This system of equations first appeared in the work of Jean le Rond d'Alembert
Jean le Rond d'Alembert
Jean-Baptiste le Rond d'Alembert was a French mathematician, mechanician, physicist, philosopher, and music theorist. He was also co-editor with Denis Diderot of the Encyclopédie...
. Later, Leonhard Euler
Leonhard Euler
Leonhard Euler was a pioneering Swiss mathematician and physicist. He made important discoveries in fields as diverse as infinitesimal calculus and graph theory. He also introduced much of the modern mathematical terminology and notation, particularly for mathematical analysis, such as the notion...
connected this system to the analytic functions . then used these equations to construct his theory of functions. Riemann's dissertation on the theory of functions appeared in 1851.
The Cauchy–Riemann equations on a pair of real-valued functions of two real variables u(x,y) and v(x,y) are the two equations:
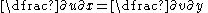
and
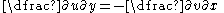
Typically u and v are taken to be the real and imaginary parts respectively of a complex
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
-valued function of a single complex variable z=x+iy, f(x + iy) = u(x,y) + iv(x,y). Suppose that u and v are real-differentiable at a point in an open subset of
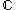 , which can be considered as functions from
, which can be considered as functions from 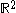 to
to 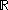 . This implies that the partial derivatives of u and v exist (although they need not be continuous) and we can approximate small variations of f linearly. Then f = u + iv is complex-differentiable at that point if and only if the partial derivatives of u and v satisfy the Cauchy–Riemann equations (1a) and (1b) at that point. The sole existence of partial derivatives satisfying the Cauchy-Riemann equations is not enough to ensure complex differentiability at that point. It is necessary to make sure that u and v are real differentiable, which is a stronger condition than the existence of the partial derivatives but it is not necessary to require continuity of these partial derivatives.
. This implies that the partial derivatives of u and v exist (although they need not be continuous) and we can approximate small variations of f linearly. Then f = u + iv is complex-differentiable at that point if and only if the partial derivatives of u and v satisfy the Cauchy–Riemann equations (1a) and (1b) at that point. The sole existence of partial derivatives satisfying the Cauchy-Riemann equations is not enough to ensure complex differentiability at that point. It is necessary to make sure that u and v are real differentiable, which is a stronger condition than the existence of the partial derivatives but it is not necessary to require continuity of these partial derivatives.Holomorphy is the property of a complex function of being differentiable at every point of an open and connected subset of
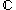 (this is called a domain in
(this is called a domain in 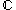 ). Consequently, we can assert that a complex function f, whose real and imaginary parts u and v are real-differentiable functions, is holomorphic if and only if, equations (1a) and (1b) are satisfied throughout the domain we are dealing with.
). Consequently, we can assert that a complex function f, whose real and imaginary parts u and v are real-differentiable functions, is holomorphic if and only if, equations (1a) and (1b) are satisfied throughout the domain we are dealing with.The reason why Euler and some other authors relate the Cauchy-Riemann equations with analyticity
Analytic function
In mathematics, an analytic function is a function that is locally given by a convergent power series. There exist both real analytic functions and complex analytic functions, categories that are similar in some ways, but different in others...
is that a major theorem in complex analysis
Complex analysis
Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is useful in many branches of mathematics, including number theory and applied mathematics; as well as in physics,...
says that holomorphic functions are analytic
Holomorphic functions are analytic
In complex analysis, a branch of mathematics, a complex-valued function ƒ of a complex variable z.*is said to be holomorphic at a point a if it is differentiable at every point within some open disk centered at a, and...
and viceversa. This means that, in complex analysis, a function that is complex-differentiable in a whole domain (holomorphic) is the same as an analytic function. This is not true for real differentiable functions.
Interpretation and reformulation
The equations are one way of looking at the condition on a function to be differentiable in the sense of complex analysisComplex analysis
Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is useful in many branches of mathematics, including number theory and applied mathematics; as well as in physics,...
: in other words they encapsulate the notion of function of a complex variable by means of conventional differential calculus
Differential calculus
In mathematics, differential calculus is a subfield of calculus concerned with the study of the rates at which quantities change. It is one of the two traditional divisions of calculus, the other being integral calculus....
. In the theory there are several other major ways of looking at this notion, and the translation of the condition into other language is often needed.
Conformal mappings
First, the Cauchy–Riemann equations may be written in complex form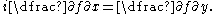
In this form, the equations correspond structurally to the condition that the Jacobian matrix is of the form
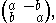
where
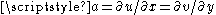 and
and 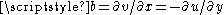 . A matrix of this form is the matrix representation of a complex number. Geometrically, such a matrix is always the composition
. A matrix of this form is the matrix representation of a complex number. Geometrically, such a matrix is always the compositionFunction composition
In mathematics, function composition is the application of one function to the results of another. For instance, the functions and can be composed by computing the output of g when it has an argument of f instead of x...
of a rotation
Rotation
A rotation is a circular movement of an object around a center of rotation. A three-dimensional object rotates always around an imaginary line called a rotation axis. If the axis is within the body, and passes through its center of mass the body is said to rotate upon itself, or spin. A rotation...
with a scaling, and in particular preserves angle
Angle
In geometry, an angle is the figure formed by two rays sharing a common endpoint, called the vertex of the angle.Angles are usually presumed to be in a Euclidean plane with the circle taken for standard with regard to direction. In fact, an angle is frequently viewed as a measure of an circular arc...
s. Consequently, a function satisfying the Cauchy–Riemann equations, with a nonzero derivative, preserves the angle between curves in the plane. That is, the Cauchy–Riemann equations are the conditions for a function to be conformal
Conformal map
In mathematics, a conformal map is a function which preserves angles. In the most common case the function is between domains in the complex plane.More formally, a map,...
.
Complex differentiability
Suppose thatf(z) = u(z) + i v(z)
is a function of a complex number z. Then the complex derivative of ƒ at a point zis defined by
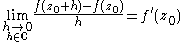
provided this limit exists.
If this limit exists, then it may be computed by taking the limit as h → 0 along the real axis or imaginary axis; in either case it should give the same result. Approaching along the real axis, one finds

On the other hand, approaching along the imaginary axis,
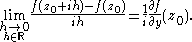
The equality of the derivative of ƒ taken along the two axes is
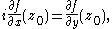
which are the Cauchy–Riemann equations (2) at the point z0.
Conversely, if ƒ : C → C is a function which is differentiable when regarded as a function on R2, then ƒ is complex differentiable if and only if the Cauchy–Riemann equations hold. In other words, if u and v are real-differentiable functions of two real variables, obviously u+iv is a (complex-valued) real-differentiable function, but u+iv is complex-differentiable if and only if the Cauchy-Riemann equations hold.
Indeed, following , suppose ƒ is a complex function defined in an open set Ω ⊂ C. Then, writing z = x + i y for every z ∈ Ω, one can also regard Ω as an open subset of R2, and ƒ as a function of two real variables x and y, which maps Ω ⊂ R2 to C. We consider the Cauchy–Riemann equations at z = 0 assuming ƒ(z) = 0, just for notational simplicity – the proof is identical in general case. So assume ƒ is differentiable at 0, as a function of two real variables from Ω to C. This is equivalent to the existence of two complex numbers
 and
and 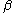 (which are the partial derivatives of ƒ) such that
(which are the partial derivatives of ƒ) such that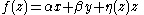
where
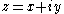 and
and 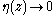 as
as 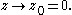 Since
Since  and
and 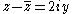 , the above can be re-written as
, the above can be re-written as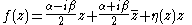
Defining the two Wirtinger derivatives
Wirtinger derivatives
In complex analysis of one and several complex variables, Wirtinger derivatives , named after Wilhelm Wirtinger who introduced them in 1927 in the course of his studies on the theory of functions of several complex variables, are partial differential operators of the first order which behave in a...
as
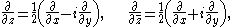
the above equality can be written as
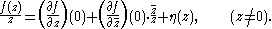
For real values of
 , we have
, we have 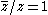 and for purely imaginary
and for purely imaginary  we have
we have 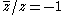 hence
hence 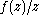 has a limit at 0 (i.e., ƒ is complex differentiable at 0) if and only if
has a limit at 0 (i.e., ƒ is complex differentiable at 0) if and only if 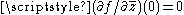 . But this is exactly the Cauchy–Riemann equations, thus ƒ is differentiable at 0 if and only if the Cauchy–Riemann equations hold at 0.
. But this is exactly the Cauchy–Riemann equations, thus ƒ is differentiable at 0 if and only if the Cauchy–Riemann equations hold at 0.Independence of the complex conjugate
The above proof suggests another interpretation of the Cauchy–Riemann equations. The complex conjugateComplex conjugate
In mathematics, complex conjugates are a pair of complex numbers, both having the same real part, but with imaginary parts of equal magnitude and opposite signs...
of z, denoted
 , is defined by
, is defined by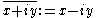
for real x and y. The Cauchy–Riemann equations can then be written as a single equation
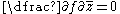
by using the Wirtinger derivative respect to the conjugate variable
Wirtinger derivatives
In complex analysis of one and several complex variables, Wirtinger derivatives , named after Wilhelm Wirtinger who introduced them in 1927 in the course of his studies on the theory of functions of several complex variables, are partial differential operators of the first order which behave in a...
. In this form, the Cauchy–Riemann equations can be interpreted as the statement that f is independent of the variable
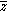 . As such, we can view analytic functions as true functions of one complex variable as opposed to complex functions of two real variables.
. As such, we can view analytic functions as true functions of one complex variable as opposed to complex functions of two real variables.Physical interpretation
One interpretation of the Cauchy–Riemann equations does not involve complex variables directly. Suppose that u and v satisfy the Cauchy–Riemann equations in an open subset of R2, and consider the vector fieldVector field
In vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...
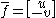
regarded as a (real) two-component vector. Then the second Cauchy–Riemann equation (1b) asserts that
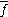 is irrotational
is irrotationalIrrotational vector field
In vector calculus a conservative vector field is a vector field which is the gradient of a function, known in this context as a scalar potential. Conservative vector fields have the property that the line integral from one point to another is independent of the choice of path connecting the two...
:

The first Cauchy–Riemann equation (1a) asserts that the vector field is solenoidal (or divergence
Divergence
In vector calculus, divergence is a vector operator that measures the magnitude of a vector field's source or sink at a given point, in terms of a signed scalar. More technically, the divergence represents the volume density of the outward flux of a vector field from an infinitesimal volume around...
-free):
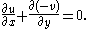
Owing respectively to Green's theorem
Green's theorem
In mathematics, Green's theorem gives the relationship between a line integral around a simple closed curve C and a double integral over the plane region D bounded by C...
and the divergence theorem
Divergence theorem
In vector calculus, the divergence theorem, also known as Gauss' theorem , Ostrogradsky's theorem , or Gauss–Ostrogradsky theorem is a result that relates the flow of a vector field through a surface to the behavior of the vector field inside the surface.More precisely, the divergence theorem...
, such a field is necessarily conserved and free from sources or sinks, having net flux equal to zero through any open domain. (These two observations combine as real and imaginary parts in Cauchy's integral theorem
Cauchy's integral theorem
In mathematics, the Cauchy integral theorem in complex analysis, named after Augustin-Louis Cauchy, is an important statement about line integrals for holomorphic functions in the complex plane...
.) In fluid dynamics
Fluid dynamics
In physics, fluid dynamics is a sub-discipline of fluid mechanics that deals with fluid flow—the natural science of fluids in motion. It has several subdisciplines itself, including aerodynamics and hydrodynamics...
, such a vector field is a potential flow
Potential flow
In fluid dynamics, potential flow describes the velocity field as the gradient of a scalar function: the velocity potential. As a result, a potential flow is characterized by an irrotational velocity field, which is a valid approximation for several applications...
. In magnetostatics
Magnetostatics
Magnetostatics is the study of magnetic fields in systems where the currents are steady . It is the magnetic analogue of electrostatics, where the charges are stationary. The magnetization need not be static; the equations of magnetostatics can be used to predict fast magnetic switching events that...
, such vector fields model static magnetic field
Magnetic field
A magnetic field is a mathematical description of the magnetic influence of electric currents and magnetic materials. The magnetic field at any given point is specified by both a direction and a magnitude ; as such it is a vector field.Technically, a magnetic field is a pseudo vector;...
s on a region of the plane containing no current. In electrostatics
Electrostatics
Electrostatics is the branch of physics that deals with the phenomena and properties of stationary or slow-moving electric charges....
, they model static electric fields in a region of the plane containing no electric charge.
Other representations
Other representations of the Cauchy–Riemann equations occasionally arise in other coordinate systemCoordinate system
In geometry, a coordinate system is a system which uses one or more numbers, or coordinates, to uniquely determine the position of a point or other geometric element. The order of the coordinates is significant and they are sometimes identified by their position in an ordered tuple and sometimes by...
s. If (1a) and (1b) hold for a differentiable pair of functions u and v, then so do
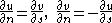
for any coordinate system such that the pair
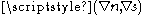 is orthonormal and positively oriented
is orthonormal and positively orientedOrientation (mathematics)
In mathematics, orientation is a notion that in two dimensions allows one to say when a cycle goes around clockwise or counterclockwise, and in three dimensions when a figure is left-handed or right-handed. In linear algebra, the notion of orientation makes sense in arbitrary dimensions...
. As a consequence, in particular, in the system of coordinates given by the polar representation , the equations then take the form
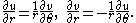
Combining these into one equation for ƒ gives
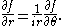
Inhomogeneous equations
The inhomogeneous Cauchy–Riemann equations consist of the two equations for a pair of unknown functions u(x,y) and v(x,y) of two real variables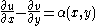
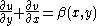
for some given functions α(x,y) and β(x,y) defined in an open subset of R2. These equations are usually combined into a single equation
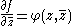
where f = u + iv and φ = (α + iβ)/2.
If φ is Ck, then the inhomogeneous equation is explicitly solvable in any bounded domain D, provided φ is continuous on the closure
Closure (topology)
In mathematics, the closure of a subset S in a topological space consists of all points in S plus the limit points of S. Intuitively, these are all the points that are "near" S. A point which is in the closure of S is a point of closure of S...
of D. Indeed, by the Cauchy integral formula,
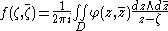
for all ζ ∈ D.
Goursat's theorem and its generalizations
Suppose that is a complex-valued function which is differentiableFréchet derivative
In mathematics, the Fréchet derivative is a derivative defined on Banach spaces. Named after Maurice Fréchet, it is commonly used to formalize the concept of the functional derivative used widely in the calculus of variations. Intuitively, it generalizes the idea of linear approximation from...
as a function . Then Goursat's theorem asserts that ƒ is analytic in an open complex domain Ω if and only if it satisfies the Cauchy–Riemann equation in the domain . In particular, continuous differentiability of ƒ need not be assumed .
The hypotheses of Goursat's theorem can be weakened significantly. If is continuous in an open set Ω and the partial derivative
Partial derivative
In mathematics, a partial derivative of a function of several variables is its derivative with respect to one of those variables, with the others held constant...
s of ƒ with respect to x and y exist in Ω, and satisfies the Cauchy–Riemann equations throughout Ω, then ƒ is holomorphic (and thus analytic). This result is the Looman–Menchoff theorem
Looman–Menchoff theorem
In the mathematical field of complex analysis, the Looman–Menchoff theorem states that a continuous complex-valued function defined in an open set of the complex plane is holomorphic if and only if it satisfies the Cauchy–Riemann equations...
.
The hypothesis that ƒ obey the Cauchy–Riemann equations throughout the domain Ω is essential. It is possible to construct a continuous function satisfying the Cauchy–Riemann equations at a point, but which is not analytic at the point (e.g., ƒ(z) = . Similarly, some additional assumption is needed besides the Cauchy–Riemann equations (such as continuity), as the following example illustrates
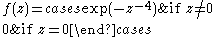
which satisfies the Cauchy–Riemann equations everywhere, but fails to be continuous at z = 0.
Nevertheless, if a function satisfies the Cauchy–Riemann equations in an open set in a weak sense
Weak derivative
In mathematics, a weak derivative is a generalization of the concept of the derivative of a function for functions not assumed differentiable, but only integrable, i.e. to lie in the Lebesgue space L^1. See distributions for an even more general definition.- Definition :Let u be a function in the...
, then the function is analytic. More precisely :
- If ƒ(z) is locally integrable in an open domain Ω ⊂ C, and satisfies the Cauchy–Riemann equations weakly, then ƒ agrees almost everywhereAlmost everywhereIn measure theory , a property holds almost everywhere if the set of elements for which the property does not hold is a null set, that is, a set of measure zero . In cases where the measure is not complete, it is sufficient that the set is contained within a set of measure zero...
with an analytic function in Ω.
This is in fact a special case of a more general result on the regularity of solutions of hypoelliptic partial differential equations.
Several variables
There are Cauchy–Riemann equations, appropriately generalized, in the theory of several complex variablesSeveral complex variables
The theory of functions of several complex variables is the branch of mathematics dealing with functionson the space Cn of n-tuples of complex numbers...
. They form a significant overdetermined system
Overdetermined system
In mathematics, a system of linear equations is considered overdetermined if there are more equations than unknowns. The terminology can be described in terms of the concept of counting constraints. Each unknown can be seen as an available degree of freedom...
of PDEs. As often formulated, the d-bar operator
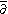
annihilates holomorphic functions. This generalizes most directly the formulation
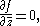
where

Bäcklund transform
Viewed as conjugate harmonic functions, the Cauchy–Riemann equations are a simple example of a Bäcklund transformBäcklund transform
In mathematics, Bäcklund transforms or Bäcklund transformations relate partial differential equations and their solutions. They are an important tool in soliton theory and integrable systems...
. More complicated, generally non-linear Bäcklund transforms, such as in the sine-Gordon equation
Sine-Gordon equation
The sine–Gordon equation is a nonlinear hyperbolic partial differential equation in 1 + 1 dimensions involving the d'Alembert operator and the sine of the unknown function. It was originally considered in the nineteenth century in the course of study of surfaces of constant negative...
, are of great interest in the theory of soliton
Soliton
In mathematics and physics, a soliton is a self-reinforcing solitary wave that maintains its shape while it travels at constant speed. Solitons are caused by a cancellation of nonlinear and dispersive effects in the medium...
s and integrable system
Integrable system
In mathematics and physics, there are various distinct notions that are referred to under the name of integrable systems.In the general theory of differential systems, there is Frobenius integrability, which refers to overdetermined systems. In the classical theory of Hamiltonian dynamical...
s.

