Sine-Gordon equation
Encyclopedia
The sine–Gordon equation is a nonlinear hyperbolic partial differential equation
in 1 + 1 dimensions involving the d'Alembert operator
and the sine of the unknown function. It was originally considered in the nineteenth century in the course of study of surfaces of constant negative curvature
. This equation attracted a lot of attention in the 1970s due to the presence of soliton
solutions.
) space-time coordinates, denoted (x, t), the equation reads
Passing to the light cone coordinates (u, v), akin to asymptotic coordinates where
the equation takes the form:
This is the original form of the sine–Gordon equation, as it was considered in the nineteenth century in the course of investigation of surfaces
of constant Gaussian curvature
K = −1, also called pseudospherical surfaces. Choose a coordinate system for such a surface in which the coordinate mesh u = constant, v = constant is given by the asymptotic line
s parameterized with respect to the arc length. The first fundamental form
of the surface in these coordinates has a special form
where φ expresses the angle between the asymptotic lines, and for the second fundamental form, L = N = 0. Then the Codazzi-Mainardi equation expressing a compatibility condition between the first and second fundamental forms results in the sine–Gordon equation. The study of this equation and of the associated transformations of pseudospherical surfaces in the 19th century by Bianchi
and Bäcklund
led to the discovery of Bäcklund transformations.
The name "sine–Gordon equation" is a pun on the well-known Klein–Gordon equation in physics:
The sine–Gordon equation is the Euler–Lagrange equation of the field whose Lagrangian density is given by
Using the Taylor series expansion of the cosine in the Lagrangian,
it can be rewritten as the Klein–Gordon Lagrangian plus higher order terms
and multisoliton solutions.
solutions:
where
The 1-soliton solution for which we have chosen the positive root for
is called a kink, and represents a twist in the variable 
which takes the system from one solution 
to an adjacent with 
. The states 
are known as vacuum states as they are constant solutions of zero energy. The 1-soliton solution in which we take the negative root for 
is called an antikink. The form of the 1-soliton solutions can be obtained through application of a Bäcklund transform to the trivial (constant vacuum) solution and the integration of the resulting first-order differentials:
for all time.
The 1-soliton solutions can be visualized with the use of the elastic ribbon sine–Gordon model as discussed by Dodd and co-workers. Here we take a clockwise (left-handed
) twist of the elastic ribbon to be a kink with topological charge
. The alternative counterclockwise (right-handed
) twist with topological charge
will be an antikink.
solutions can be obtained through continued application of the Bäcklund transform
to the 1-soliton solution, as prescribed by a Bianchi lattice relating the transformed results. The 2-soliton solutions of the sine–Gordon equation show some of the characteristic features of the solitons. The traveling sine–Gordon kinks and/or antikinks pass through each other as if perfectly permeable, and the only observed effect is a phase shift
. Since the colliding solitons recover their velocity
and shape
such kind of interaction
is called an elastic collision
.
Another interesting 2-soliton solutions arise from the possibility of coupled kink-antikink behaviour known as a breather
. There are known three types of breathers: standing breather, traveling large amplitude breather, and traveling small amplitude breather.
the shift of the breather
is given by:
where
is the velocity of the kink, and 
is the breather's frequency. If the old position of the standing breather is 
, after the collision the new position will be 
.
This is the Euler–Lagrange equation of the Lagrangian
Another closely related equation is the elliptic sine–Gordon equation, given by
where
is now a function of the variables x and y. This is no longer a soliton equation, but it has many similar properties, as it is related to the sine–Gordon equation by the analytic continuation
(or Wick rotation
) y = it.
The elliptic sinh–Gordon equation may be defined in a similar way.
A generalization is given by Toda field theory
.
. The particle spectrum consists of a soliton, an anti-soliton and a finite (possibly zero) number of breathers. The number of the breathers depends on the value of the parameter. Multi particle productions cancels on mass shell. Vanishing of two into four amplitude was explicitly checked in one loop approximation.
Semi-classical quantization of the sine–Gordon model was done by Ludwig Faddeev and Vladimir Korepin
. Exact quantum scattering matrix was discovered by Alexander Zamolodchikov
.
This model is S-dual
to the Thirring model
.
Partial differential equation
In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
in 1 + 1 dimensions involving the d'Alembert operator
D'Alembert operator
In special relativity, electromagnetism and wave theory, the d'Alembert operator , also called the d'Alembertian or the wave operator, is the Laplace operator of Minkowski space. The operator is named for French mathematician and physicist Jean le Rond d'Alembert...
and the sine of the unknown function. It was originally considered in the nineteenth century in the course of study of surfaces of constant negative curvature
Pseudosphere
In geometry, the term pseudosphere is used to describe various surfaces with constant negative gaussian curvature. Depending on context, it can refer to either a theoretical surface of constant negative curvature, to a tractricoid, or to a hyperboloid....
. This equation attracted a lot of attention in the 1970s due to the presence of soliton
Soliton
In mathematics and physics, a soliton is a self-reinforcing solitary wave that maintains its shape while it travels at constant speed. Solitons are caused by a cancellation of nonlinear and dispersive effects in the medium...
solutions.
Origin of the equation and its name
There are two equivalent forms of the sine–Gordon equation. In the (realReal number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
) space-time coordinates, denoted (x, t), the equation reads
Passing to the light cone coordinates (u, v), akin to asymptotic coordinates where
the equation takes the form:
This is the original form of the sine–Gordon equation, as it was considered in the nineteenth century in the course of investigation of surfaces
Differential geometry of surfaces
In mathematics, the differential geometry of surfaces deals with smooth surfaces with various additional structures, most often, a Riemannian metric....
of constant Gaussian curvature
Gaussian curvature
In differential geometry, the Gaussian curvature or Gauss curvature of a point on a surface is the product of the principal curvatures, κ1 and κ2, of the given point. It is an intrinsic measure of curvature, i.e., its value depends only on how distances are measured on the surface, not on the way...
K = −1, also called pseudospherical surfaces. Choose a coordinate system for such a surface in which the coordinate mesh u = constant, v = constant is given by the asymptotic line
Asymptotic curve
In the differential geometry of surfaces, an asymptotic curve is a curve always tangent to an asymptotic direction of the surface . It is sometimes called an asymptotic line, although it need not be a line....
s parameterized with respect to the arc length. The first fundamental form
First fundamental form
In differential geometry, the first fundamental form is the inner product on the tangent space of a surface in three-dimensional Euclidean space which is induced canonically from the dot product of R3. It permits the calculation of curvature and metric properties of a surface such as length and...
of the surface in these coordinates has a special form
where φ expresses the angle between the asymptotic lines, and for the second fundamental form, L = N = 0. Then the Codazzi-Mainardi equation expressing a compatibility condition between the first and second fundamental forms results in the sine–Gordon equation. The study of this equation and of the associated transformations of pseudospherical surfaces in the 19th century by Bianchi
Luigi Bianchi
- External links :* offers translations of some of Bianchi's papers, plus a biography of Bianchi.* PDF copy at * * * *...
and Bäcklund
Albert Victor Bäcklund
Albert Victor Bäcklund was a Swedish mathematician and physicist. He was a professor at Lund University and its rector from 1907 to 1909....
led to the discovery of Bäcklund transformations.
The name "sine–Gordon equation" is a pun on the well-known Klein–Gordon equation in physics:
The sine–Gordon equation is the Euler–Lagrange equation of the field whose Lagrangian density is given by
Using the Taylor series expansion of the cosine in the Lagrangian,
it can be rewritten as the Klein–Gordon Lagrangian plus higher order terms
Soliton solutions
An interesting feature of the sine–Gordon equation is the existence of solitonSoliton
In mathematics and physics, a soliton is a self-reinforcing solitary wave that maintains its shape while it travels at constant speed. Solitons are caused by a cancellation of nonlinear and dispersive effects in the medium...
and multisoliton solutions.
1-soliton solutions
The sine–Gordon equation has the following 1-solitonSoliton
In mathematics and physics, a soliton is a self-reinforcing solitary wave that maintains its shape while it travels at constant speed. Solitons are caused by a cancellation of nonlinear and dispersive effects in the medium...
solutions:
where
The 1-soliton solution for which we have chosen the positive root for
is called a kink, and represents a twist in the variable which takes the system from one solution to an adjacent with . The states are known as vacuum states as they are constant solutions of zero energy. The 1-soliton solution in which we take the negative root for is called an antikink. The form of the 1-soliton solutions can be obtained through application of a Bäcklund transform to the trivial (constant vacuum) solution and the integration of the resulting first-order differentials:for all time.
The 1-soliton solutions can be visualized with the use of the elastic ribbon sine–Gordon model as discussed by Dodd and co-workers. Here we take a clockwise (left-handed
Right-hand rule
In mathematics and physics, the right-hand rule is a common mnemonic for understanding notation conventions for vectors in 3 dimensions. It was invented for use in electromagnetism by British physicist John Ambrose Fleming in the late 19th century....
) twist of the elastic ribbon to be a kink with topological charge
. The alternative counterclockwise (right-handedRight-hand rule
In mathematics and physics, the right-hand rule is a common mnemonic for understanding notation conventions for vectors in 3 dimensions. It was invented for use in electromagnetism by British physicist John Ambrose Fleming in the late 19th century....
) twist with topological charge
will be an antikink.  |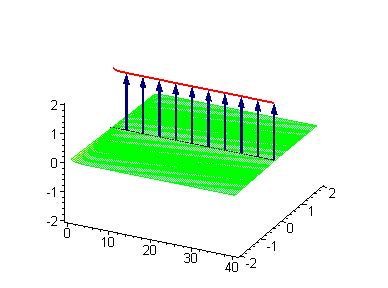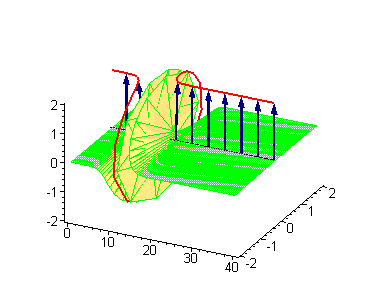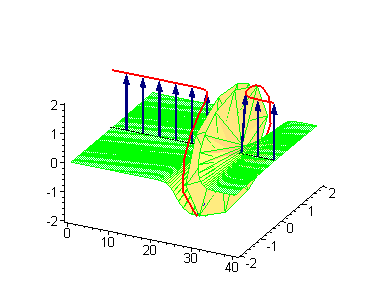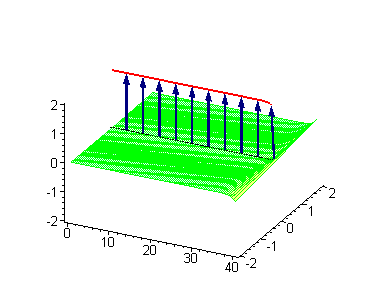
 |
2-soliton solutions
Multi-solitonSoliton
In mathematics and physics, a soliton is a self-reinforcing solitary wave that maintains its shape while it travels at constant speed. Solitons are caused by a cancellation of nonlinear and dispersive effects in the medium...
solutions can be obtained through continued application of the Bäcklund transform
Bäcklund transform
In mathematics, Bäcklund transforms or Bäcklund transformations relate partial differential equations and their solutions. They are an important tool in soliton theory and integrable systems...
to the 1-soliton solution, as prescribed by a Bianchi lattice relating the transformed results. The 2-soliton solutions of the sine–Gordon equation show some of the characteristic features of the solitons. The traveling sine–Gordon kinks and/or antikinks pass through each other as if perfectly permeable, and the only observed effect is a phase shift
Phase (waves)
Phase in waves is the fraction of a wave cycle which has elapsed relative to an arbitrary point.-Formula:The phase of an oscillation or wave refers to a sinusoidal function such as the following:...
. Since the colliding solitons recover their velocity
Velocity
In physics, velocity is speed in a given direction. Speed describes only how fast an object is moving, whereas velocity gives both the speed and direction of the object's motion. To have a constant velocity, an object must have a constant speed and motion in a constant direction. Constant ...
and shape
Shape
The shape of an object located in some space is a geometrical description of the part of that space occupied by the object, as determined by its external boundary – abstracting from location and orientation in space, size, and other properties such as colour, content, and material...
such kind of interaction
Interaction
Interaction is a kind of action that occurs as two or more objects have an effect upon one another. The idea of a two-way effect is essential in the concept of interaction, as opposed to a one-way causal effect...
is called an elastic collision
Elastic collision
An elastic collision is an encounter between two bodies in which the total kinetic energy of the two bodies after the encounter is equal to their total kinetic energy before the encounter...
.
 |
 |
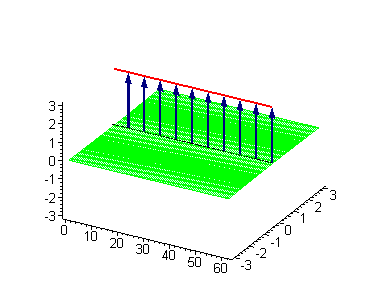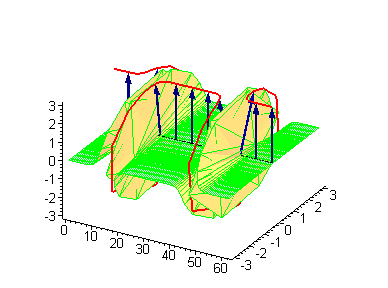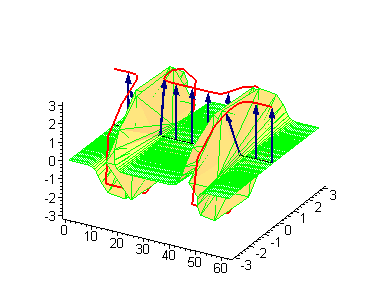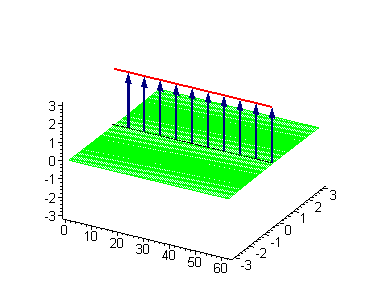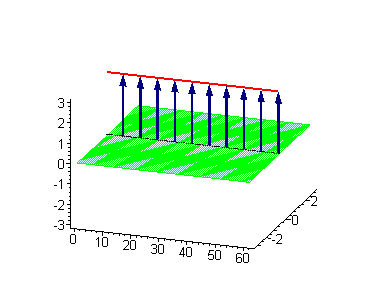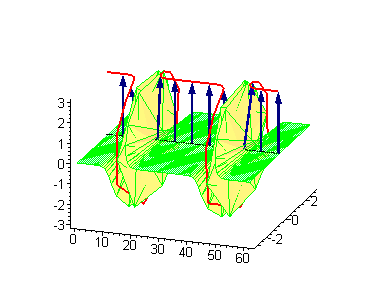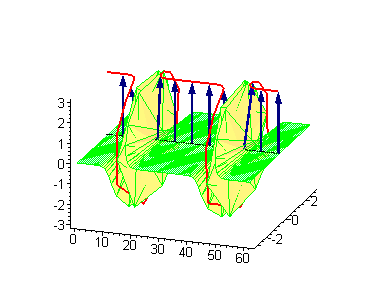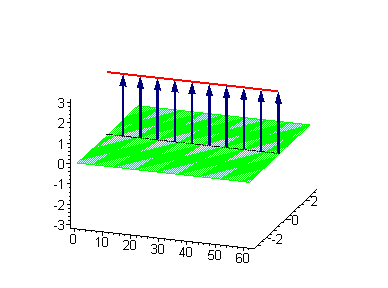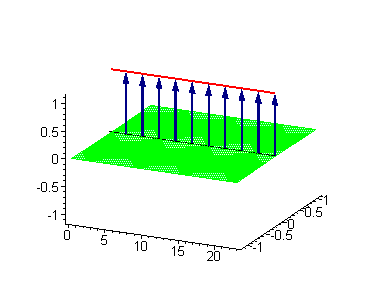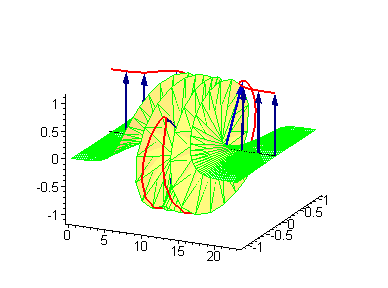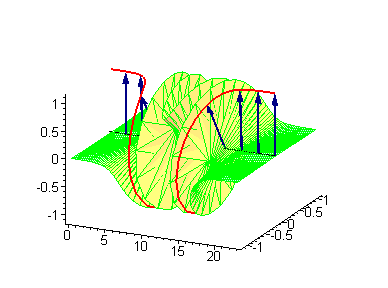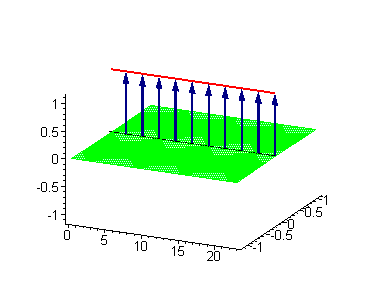
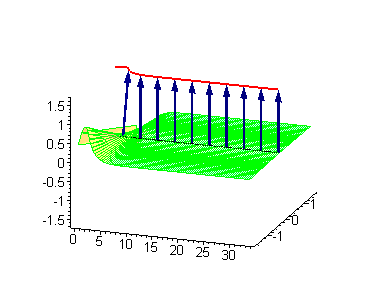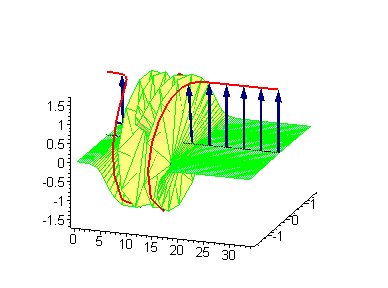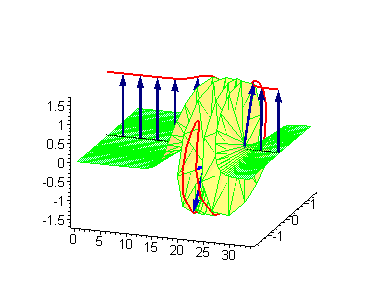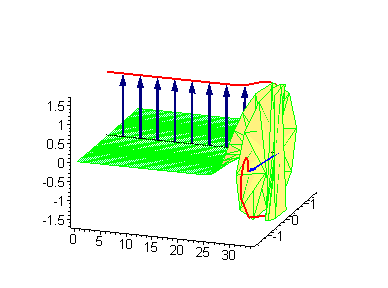
Another interesting 2-soliton solutions arise from the possibility of coupled kink-antikink behaviour known as a breather
Breather
A breather is a nonlinear wave in which energy concentrates in a localized and oscillatory fashion. This contradicts with the expectations derived from the corresponding linear system for infinitesimal amplitudes, which tends towards an even distribution of initially localized energy.A discrete...
. There are known three types of breathers: standing breather, traveling large amplitude breather, and traveling small amplitude breather.
 |
 |
 |
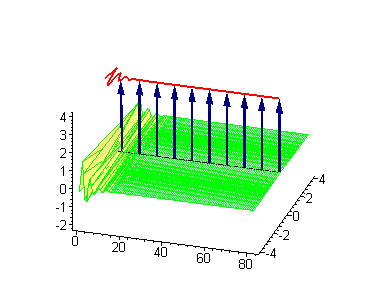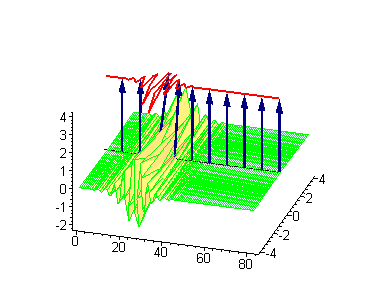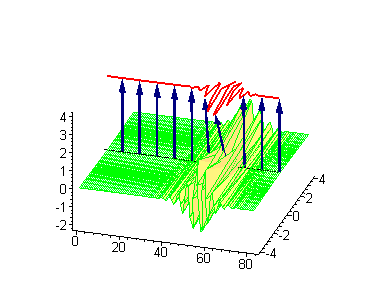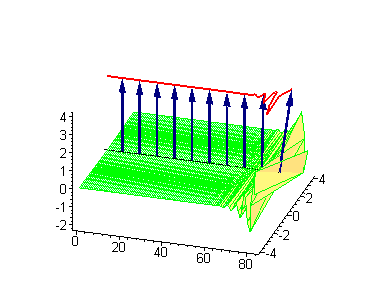3-soliton solutions
3-soliton collisions between a traveling kink and a standing breather or a traveling antikink and a standing breather results in a phase shift of the standing breather. In the process of collision between a moving kink and a standing breather,the shift of the breather
is given by:
where
is the velocity of the kink, and is the breather's frequency. If the old position of the standing breather is , after the collision the new position will be .  |
 |
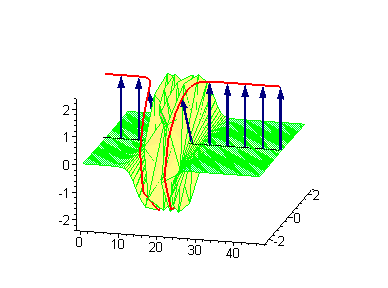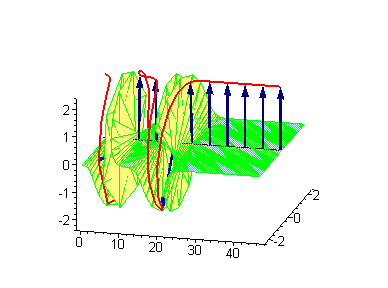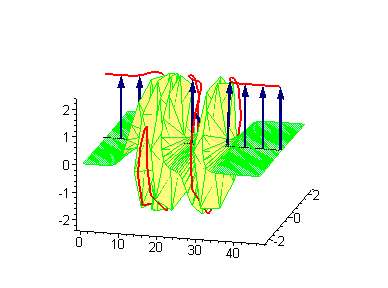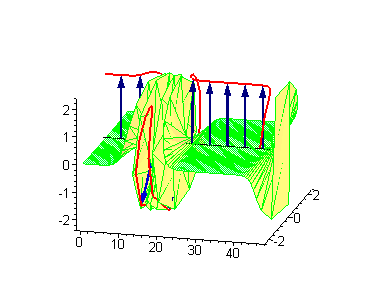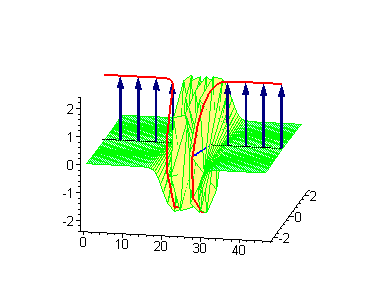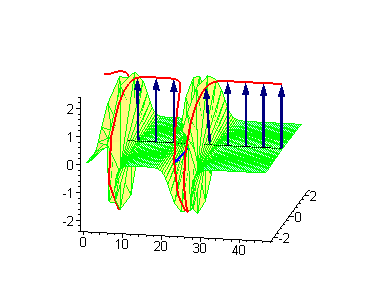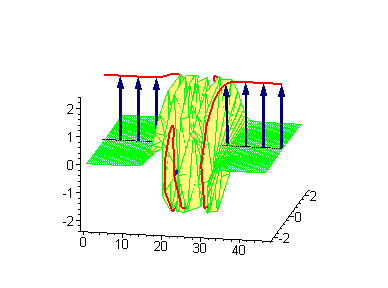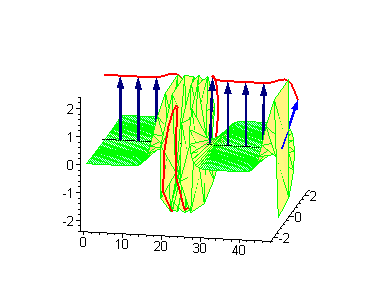Related equations
The is given byThis is the Euler–Lagrange equation of the Lagrangian
Lagrangian
The Lagrangian, L, of a dynamical system is a function that summarizes the dynamics of the system. It is named after Joseph Louis Lagrange. The concept of a Lagrangian was originally introduced in a reformulation of classical mechanics by Irish mathematician William Rowan Hamilton known as...
Another closely related equation is the elliptic sine–Gordon equation, given by
where
is now a function of the variables x and y. This is no longer a soliton equation, but it has many similar properties, as it is related to the sine–Gordon equation by the analytic continuationAnalytic continuation
In complex analysis, a branch of mathematics, analytic continuation is a technique to extend the domain of a given analytic function. Analytic continuation often succeeds in defining further values of a function, for example in a new region where an infinite series representation in terms of which...
(or Wick rotation
Wick rotation
In physics, Wick rotation, named after Gian-Carlo Wick, is a method of finding a solution to a mathematical problem in Minkowski space from a solution to a related problem in Euclidean space by means of a transformation that substitutes an imaginary-number variable for a real-number variable...
) y = it.
The elliptic sinh–Gordon equation may be defined in a similar way.
A generalization is given by Toda field theory
Toda field theory
In the study of field theory and partial differential equations, a Toda field theory is derived from the following Lagrangian:...
.
Quantum version
In quantum field theory the sine–Gordon model contains a parameter, it can be identified with Planck constantPlanck constant
The Planck constant , also called Planck's constant, is a physical constant reflecting the sizes of energy quanta in quantum mechanics. It is named after Max Planck, one of the founders of quantum theory, who discovered it in 1899...
. The particle spectrum consists of a soliton, an anti-soliton and a finite (possibly zero) number of breathers. The number of the breathers depends on the value of the parameter. Multi particle productions cancels on mass shell. Vanishing of two into four amplitude was explicitly checked in one loop approximation.
Semi-classical quantization of the sine–Gordon model was done by Ludwig Faddeev and Vladimir Korepin
Vladimir Korepin
Vladimir Korepin is a Russian-American physicist and mathematician. He is a professor at the C. N. Yang Institute of Theoretical Physics of the State University of New York at Stony Brook...
. Exact quantum scattering matrix was discovered by Alexander Zamolodchikov
Alexander Zamolodchikov
Alexander Borissowitsch Zamolodchikov is a Russian physicist, known for his contributions to condensed matter physics and string theory.Born near Dubna,...
.
This model is S-dual
S-duality
In theoretical physics, S-duality is an equivalence of two quantum field theories or string theories. An S-duality transformation maps states and vacua with coupling constant g in one theory to states and vacua with coupling constant 1/g in the dual theory...
to the Thirring model
Thirring model
The Thirring model is an exactly solvable quantum field theory which describes the self-interactions of a Dirac field in two dimension.-Definition:The Thirring model is given by the Lagrangian density...
.
In finite volume and on a half line
One can also consider the sine–Gordon model on a circle, on a line segment, or on a half line. It is possible to find boundary conditions which preserve the integrability of the model. On a half line the spectrum contains boundary bound states in addition to the solitons and breathers.Supersymmetric sine–Gordon model
A supersymmetric extension of the sine–Gordon model also exists. Integrability preserving boundary conditions for this extension can be found as well.External links
- Sine–Gordon Equation at EqWorld: The World of Mathematical Equations.
- Sinh–Gordon Equation at EqWorld: The World of Mathematical Equations.
- Sine–Gordon equation at NEQwiki, the nonlinear equations encyclopedia.