Hypoelliptic operator
Encyclopedia
In mathematics
, more specifically in the theory of partial differential equation
s, a partial differential operator
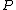defined on an open subset
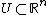
is called hypoelliptic if for every distribution
defined on an open subset 
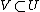such that 
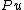is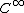 
(smooth
),
must also be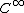 
.
If this assertion holds with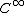
replaced by real analytic
, then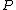
is said to be analytically hypoelliptic.
Every elliptic operator
with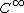
coefficients is hypoelliptic. In particular, the Laplacian is an example of a hypoelliptic operator (the Laplacian is also analytically hypoelliptic). The heat equation
operator
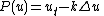
(where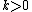
) is hypoelliptic but not elliptic. The wave equation
operator
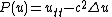
(where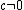
) is not hypoelliptic.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, more specifically in the theory of partial differential equation
Partial differential equation
In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables...
s, a partial differential operator
Differential operator
In mathematics, a differential operator is an operator defined as a function of the differentiation operator. It is helpful, as a matter of notation first, to consider differentiation as an abstract operation, accepting a function and returning another .This article considers only linear operators,...
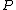defined on an open subset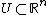is called hypoelliptic if for every distribution
Distribution (mathematics)
In mathematical analysis, distributions are objects that generalize functions. Distributions make it possible to differentiate functions whose derivatives do not exist in the classical sense. In particular, any locally integrable function has a distributional derivative...
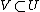defined on an open subset such that 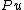is 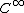(smoothSmooth function
In mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
),
must also be 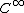.If this assertion holds with
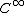replaced by real analyticMathematical analysis
Mathematical analysis, which mathematicians refer to simply as analysis, has its beginnings in the rigorous formulation of infinitesimal calculus. It is a branch of pure mathematics that includes the theories of differentiation, integration and measure, limits, infinite series, and analytic functions...
, then
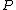is said to be analytically hypoelliptic.Every elliptic operator
Elliptic operator
In the theory of partial differential equations, elliptic operators are differential operators that generalize the Laplace operator. They are defined by the condition that the coefficients of the highest-order derivatives be positive, which implies the key property that the principal symbol is...
with
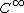coefficients is hypoelliptic. In particular, the Laplacian is an example of a hypoelliptic operator (the Laplacian is also analytically hypoelliptic). The heat equationHeat equation
The heat equation is an important partial differential equation which describes the distribution of heat in a given region over time...
operator
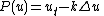
(where
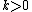) is hypoelliptic but not elliptic. The wave equationWave equation
The wave equation is an important second-order linear partial differential equation for the description of waves – as they occur in physics – such as sound waves, light waves and water waves. It arises in fields like acoustics, electromagnetics, and fluid dynamics...
operator
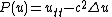
(where
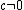) is not hypoelliptic.