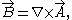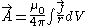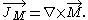Magnetostatics
Encyclopedia
Magnetostatics is the study of magnetic field
s in systems where the currents are steady (not changing with time). It is the magnetic analogue of electrostatics, where the charges are stationary. The magnetization need not be static; the equations of magnetostatics can be used to predict fast magnetic switching
events that occur on time scales of nanoseconds or less. Magnetostatics is even a good approximation when the currents are not static — as long as the currents do not alternate rapidly. Magnetostatics is widely used in applications of micromagnetics such as models of magnetic recording devices.
and assuming that charges are either fixed or move as a steady current
, the equations separate into two equations for the electric field
(see electrostatics
) and two for the magnetic field
. The fields are independent of time and each other. The magnetostatic equations, in both differential and integral forms, are shown in the table below.
The first integral is over a surface
with oriented surface element 
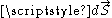. The second is a line integral around a closed loop 
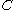with line element 
. The current going through the loop is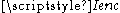 
.
The quality of this approximation may be guessed by comparing the above equations with the full version of Maxwell's equations
and considering the importance of the terms that have been removed. Of particular significance is the comparison of the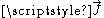
term against the 
term. If the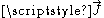 
term is substantially larger, then the smaller term may be ignored without significant loss of accuracy.
. Plugging this result into Faraday's Law
finds a value for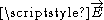
(which had previously been ignored). This method is not a true solution of Maxwell's equations
but can provide a good approximation for slowly changing fields.
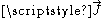is available) then
the magnetic field can be determined from the currents by the Biot-Savart
equation:
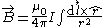
This technique works well for problems where the medium is a vacuum
or air or some similar material with a relative permeability
of 1. This includes Air core inductors and Air core transformers. One advantage of this technique is that a complex coil geometry can be integrated in sections, or for a very difficult geometry numerical integration
may be used. Since this equation is primarily used to solve linear
problems, the complete answer will be a sum of the integral of each component section.
For problems where the dominant magnetic material is a highly permeable magnetic core
with relatively small air gaps, a magnetic circuit
approach is useful. When the air gaps are large in comparison to the magnetic circuit
length, fringing becomes significant and usually requires a finite element calculation. The finite element calculation uses a modified form of the magnetostatic equations above in order to calculate magnetic potential
. The value of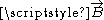
can be found from the magnetic potential
.
The magnetic field can be derived from the vector potential
. Since the divergence of the magnetic flux density is always zero,
and the relation of the vector potential to current is:
where
is the current density
.
that is primarily due to electron spins
. In such materials the magnetization must be explicitly included using the relation
Except in metals, electric currents can be ignored. Then Ampère's law is simply
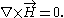
This has the general solution
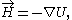
where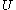
is a scalar potential
. Substituting this in Gauss's law gives
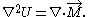
Thus, the divergence of the magnetization,
has a role analogous to the electric charge in electrostatics and is often referred to as an effective charge density 
.
The vector potential method can also be employed with an effective current density
Magnetic field
A magnetic field is a mathematical description of the magnetic influence of electric currents and magnetic materials. The magnetic field at any given point is specified by both a direction and a magnitude ; as such it is a vector field.Technically, a magnetic field is a pseudo vector;...
s in systems where the currents are steady (not changing with time). It is the magnetic analogue of electrostatics, where the charges are stationary. The magnetization need not be static; the equations of magnetostatics can be used to predict fast magnetic switching
Magnetization reversal
Magnetization reversal, or switching, represents the process that leads to a 180° reorientation of the magnetization vector with respect to its initial direction, from one stable orientation to the opposite one. Technologically, this is one of the most important processes in magnetism that is...
events that occur on time scales of nanoseconds or less. Magnetostatics is even a good approximation when the currents are not static — as long as the currents do not alternate rapidly. Magnetostatics is widely used in applications of micromagnetics such as models of magnetic recording devices.
Magnetostatics as a special case of Maxwell's equations
Starting from Maxwell's equationsMaxwell's equations
Maxwell's equations are a set of partial differential equations that, together with the Lorentz force law, form the foundation of classical electrodynamics, classical optics, and electric circuits. These fields in turn underlie modern electrical and communications technologies.Maxwell's equations...
and assuming that charges are either fixed or move as a steady current
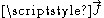, the equations separate into two equations for the electric fieldElectric field
In physics, an electric field surrounds electrically charged particles and time-varying magnetic fields. The electric field depicts the force exerted on other electrically charged objects by the electrically charged particle the field is surrounding...
(see electrostatics
Electrostatics
Electrostatics is the branch of physics that deals with the phenomena and properties of stationary or slow-moving electric charges....
) and two for the magnetic field
Magnetic field
A magnetic field is a mathematical description of the magnetic influence of electric currents and magnetic materials. The magnetic field at any given point is specified by both a direction and a magnitude ; as such it is a vector field.Technically, a magnetic field is a pseudo vector;...
. The fields are independent of time and each other. The magnetostatic equations, in both differential and integral forms, are shown in the table below.
| Name | Partial differential Partial differential equation In mathematics, partial differential equations are a type of differential equation, i.e., a relation involving an unknown function of several independent variables and their partial derivatives with respect to those variables... form |
Integral Integral Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus... form |
|---|---|---|
| Gauss's law for magnetism: |  |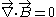
 |
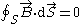| Ampère's law Ampère's law In classical electromagnetism, Ampère's circuital law, discovered by André-Marie Ampère in 1826, relates the integrated magnetic field around a closed loop to the electric current passing through the loop... : |
 |
 |
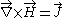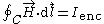The first integral is over a surface
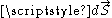with oriented surface element . The second is a line integral around a closed loop 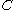with line element . The current going through the loop is 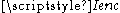.The quality of this approximation may be guessed by comparing the above equations with the full version of Maxwell's equations
Maxwell's equations
Maxwell's equations are a set of partial differential equations that, together with the Lorentz force law, form the foundation of classical electrodynamics, classical optics, and electric circuits. These fields in turn underlie modern electrical and communications technologies.Maxwell's equations...
and considering the importance of the terms that have been removed. Of particular significance is the comparison of the
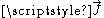term against the term. If the 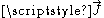term is substantially larger, then the smaller term may be ignored without significant loss of accuracy.Re-introducing Faraday's law
A common technique is to solve a series of magnetostatic problems at incremental time steps and then use these solutions to approximate the term. Plugging this result into Faraday's LawFaraday's law of induction
Faraday's law of induction dates from the 1830s, and is a basic law of electromagnetism relating to the operating principles of transformers, inductors, and many types of electrical motors and generators...
finds a value for
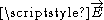(which had previously been ignored). This method is not a true solution of Maxwell's equationsMaxwell's equations
Maxwell's equations are a set of partial differential equations that, together with the Lorentz force law, form the foundation of classical electrodynamics, classical optics, and electric circuits. These fields in turn underlie modern electrical and communications technologies.Maxwell's equations...
but can provide a good approximation for slowly changing fields.
Current sources
If all currents in a system are known (i.e., if a complete description of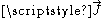 is available) thenthe magnetic field can be determined from the currents by the Biot-Savart
Biot-Savart law
The Biot–Savart law is an equation in electromagnetism that describes the magnetic field B generated by an electric current. The vector field B depends on the magnitude, direction, length, and proximity of the electric current, and also on a fundamental constant called the magnetic constant...
equation:
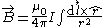
This technique works well for problems where the medium is a vacuum
Vacuum
In everyday usage, vacuum is a volume of space that is essentially empty of matter, such that its gaseous pressure is much less than atmospheric pressure. The word comes from the Latin term for "empty". A perfect vacuum would be one with no particles in it at all, which is impossible to achieve in...
or air or some similar material with a relative permeability
Permeability (electromagnetism)
In electromagnetism, permeability is the measure of the ability of a material to support the formation of a magnetic field within itself. In other words, it is the degree of magnetization that a material obtains in response to an applied magnetic field. Magnetic permeability is typically...
of 1. This includes Air core inductors and Air core transformers. One advantage of this technique is that a complex coil geometry can be integrated in sections, or for a very difficult geometry numerical integration
Numerical integration
In numerical analysis, numerical integration constitutes a broad family of algorithms for calculating the numerical value of a definite integral, and by extension, the term is also sometimes used to describe the numerical solution of differential equations. This article focuses on calculation of...
may be used. Since this equation is primarily used to solve linear
Linear
In mathematics, a linear map or function f is a function which satisfies the following two properties:* Additivity : f = f + f...
problems, the complete answer will be a sum of the integral of each component section.
For problems where the dominant magnetic material is a highly permeable magnetic core
Magnetic core
A magnetic core is a piece of magnetic material with a high permeability used to confine and guide magnetic fields in electrical, electromechanical and magnetic devices such as electromagnets, transformers, electric motors, inductors and magnetic assemblies. It is made of ferromagnetic metal such...
with relatively small air gaps, a magnetic circuit
Magnetic circuit
A magnetic circuit is made up of one or more closed loop paths containing a magnetic flux. The flux is usually generated by permanent magnets or electromagnets and confined to the path by magnetic cores consisting of ferromagnetic materials like iron, although there may be air gaps or other...
approach is useful. When the air gaps are large in comparison to the magnetic circuit
Magnetic circuit
A magnetic circuit is made up of one or more closed loop paths containing a magnetic flux. The flux is usually generated by permanent magnets or electromagnets and confined to the path by magnetic cores consisting of ferromagnetic materials like iron, although there may be air gaps or other...
length, fringing becomes significant and usually requires a finite element calculation. The finite element calculation uses a modified form of the magnetostatic equations above in order to calculate magnetic potential
Magnetic potential
The term magnetic potential can be used for either of two quantities in classical electromagnetism: the magnetic vector potential, A, and the magnetic scalar potential, ψ...
. The value of
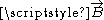can be found from the magnetic potentialMagnetic potential
The term magnetic potential can be used for either of two quantities in classical electromagnetism: the magnetic vector potential, A, and the magnetic scalar potential, ψ...
.
The magnetic field can be derived from the vector potential
Vector potential
In vector calculus, a vector potential is a vector field whose curl is a given vector field. This is analogous to a scalar potential, which is a scalar field whose negative gradient is a given vector field....
. Since the divergence of the magnetic flux density is always zero,
and the relation of the vector potential to current is:
where
is the current densityCurrent density
Current density is a measure of the density of flow of a conserved charge. Usually the charge is the electric charge, in which case the associated current density is the electric current per unit area of cross section, but the term current density can also be applied to other conserved...
.
Magnetization
Strongly magnetic materials (i.e., Ferromagnetic, Ferrimagnetic or Paramagnetic) have a magnetizationMagnetization
In classical electromagnetism, magnetization or magnetic polarization is the vector field that expresses the density of permanent or induced magnetic dipole moments in a magnetic material...
that is primarily due to electron spins
Spin (physics)
In quantum mechanics and particle physics, spin is a fundamental characteristic property of elementary particles, composite particles , and atomic nuclei.It is worth noting that the intrinsic property of subatomic particles called spin and discussed in this article, is related in some small ways,...
. In such materials the magnetization must be explicitly included using the relation
Except in metals, electric currents can be ignored. Then Ampère's law is simply
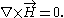
This has the general solution
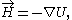
where
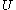is a scalar potentialPotential
*In linguistics, the potential mood*The mathematical study of potentials is known as potential theory; it is the study of harmonic functions on manifolds...
. Substituting this in Gauss's law gives
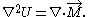
Thus, the divergence of the magnetization,
has a role analogous to the electric charge in electrostatics and is often referred to as an effective charge density .The vector potential method can also be employed with an effective current density
