
Potential flow
Encyclopedia
Fluid dynamics
In physics, fluid dynamics is a sub-discipline of fluid mechanics that deals with fluid flow—the natural science of fluids in motion. It has several subdisciplines itself, including aerodynamics and hydrodynamics...
, potential flow describes the velocity field as the gradient
Gradient
In vector calculus, the gradient of a scalar field is a vector field that points in the direction of the greatest rate of increase of the scalar field, and whose magnitude is the greatest rate of change....
of a scalar function: the velocity potential. As a result, a potential flow is characterized by an irrotational velocity field, which is a valid approximation for several applications. The irrotationality of a potential flow is due to the curl of a gradient always being equal to zero.
In the case of an incompressible flow
Incompressible flow
In fluid mechanics or more generally continuum mechanics, incompressible flow refers to flow in which the material density is constant within an infinitesimal volume that moves with the velocity of the fluid...
the velocity potential satisfies Laplace's equation
Laplace's equation
In mathematics, Laplace's equation is a second-order partial differential equation named after Pierre-Simon Laplace who first studied its properties. This is often written as:where ∆ = ∇² is the Laplace operator and \varphi is a scalar function...
, and potential theory
Potential theory
In mathematics and mathematical physics, potential theory may be defined as the study of harmonic functions.- Definition and comments :The term "potential theory" was coined in 19th-century physics, when it was realized that the fundamental forces of nature could be modeled using potentials which...
is applicable. However, potential flows also have been used to describe compressible flow
Compressible flow
Compressible flow is the area of fluid mechanics that deals with fluids in which the fluid density varies significantly in response to a change in pressure. Compressibility effects are typically considered significant if the Mach number of the flow exceeds 0.3, or if the fluid undergoes very large...
s. The potential flow approach occurs in the modeling of both stationary as well as nonstationary flows.
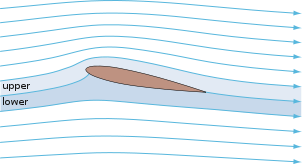
Applications of potential flow are for instance: the outer flow field for aerofoil
Airfoil
An airfoil or aerofoil is the shape of a wing or blade or sail as seen in cross-section....
s, water waves
Ocean surface wave
In fluid dynamics, wind waves or, more precisely, wind-generated waves are surface waves that occur on the free surface of oceans, seas, lakes, rivers, and canals or even on small puddles and ponds. They usually result from the wind blowing over a vast enough stretch of fluid surface. Waves in the...
, electroosmotic flow, and groundwater flow
Groundwater flow equation
Used in hydrogeology, the groundwater flow equation is the mathematical relationship which is used to describe the flow of groundwater through an aquifer. The transient flow of groundwater is described by a form of the diffusion equation, similar to that used in heat transfer to describe the flow...
.
For flows (or parts thereof) with strong vorticity effects, the potential flow approximation is not applicable.
Characteristics and applications

Description and characteristics
In fluid dynamics, a potential flow is described by means of a velocity potential φ, being a functionFunction (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
of space and time. The flow velocity
Flow velocity
In fluid dynamics the flow velocity, or velocity field, of a fluid is a vector field which is used to mathematically describe the motion of a fluid...
v is a vector field
Vector field
In vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...
equal to the gradient, ∇, of the velocity potential φ:
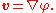
Sometimes, also the definition v = −∇φ, with a minus sign, is used. But here we will use the definition above, without the minus sign. From vector calculus it is known, that the curl of a gradient is equal to zero:

and consequently the vorticity, the curl
Curl
In vector calculus, the curl is a vector operator that describes the infinitesimal rotation of a 3-dimensional vector field. At every point in the field, the curl is represented by a vector...
of the velocity field v, is zero:

This implies that a potential flow is an irrotational flow. This has direct consequences for the applicability of potential flow. In flow regions where vorticity is known to be important, such as wake
Wake
A wake is the region of recirculating flow immediately behind a moving or stationary solid body, caused by the flow of surrounding fluid around the body.-Fluid dynamics:...
s and boundary layer
Boundary layer
In physics and fluid mechanics, a boundary layer is that layer of fluid in the immediate vicinity of a bounding surface where effects of viscosity of the fluid are considered in detail. In the Earth's atmosphere, the planetary boundary layer is the air layer near the ground affected by diurnal...
s, potential flow theory is not able to provide reasonable predictions of the flow. Fortunately, there are often large regions of a flow where the assumption of irrotationality is valid, which is why potential flow is used for various applications. For instance in: flow around aircraft
Aircraft
An aircraft is a vehicle that is able to fly by gaining support from the air, or, in general, the atmosphere of a planet. An aircraft counters the force of gravity by using either static lift or by using the dynamic lift of an airfoil, or in a few cases the downward thrust from jet engines.Although...
, groundwater flow
Groundwater flow
Groundwater flow is defined as the "...part of streamflow that has infiltrated the ground, has entered the phreatic zone, and has been discharged into a stream channel, via springs or seepage water". In hydrogeology it is measured by the Groundwater flow equation.- See also :*Subsurface...
, acoustics
Acoustics
Acoustics is the interdisciplinary science that deals with the study of all mechanical waves in gases, liquids, and solids including vibration, sound, ultrasound and infrasound. A scientist who works in the field of acoustics is an acoustician while someone working in the field of acoustics...
, water waves, and electroosmotic flow.
Incompressible flow
In case of an incompressible flowIncompressible flow
In fluid mechanics or more generally continuum mechanics, incompressible flow refers to flow in which the material density is constant within an infinitesimal volume that moves with the velocity of the fluid...
— for instance of a liquid
Liquid
Liquid is one of the three classical states of matter . Like a gas, a liquid is able to flow and take the shape of a container. Some liquids resist compression, while others can be compressed. Unlike a gas, a liquid does not disperse to fill every space of a container, and maintains a fairly...
, or a gas
Gas
Gas is one of the three classical states of matter . Near absolute zero, a substance exists as a solid. As heat is added to this substance it melts into a liquid at its melting point , boils into a gas at its boiling point, and if heated high enough would enter a plasma state in which the electrons...
at low Mach number
Mach number
Mach number is the speed of an object moving through air, or any other fluid substance, divided by the speed of sound as it is in that substance for its particular physical conditions, including those of temperature and pressure...
s; but not for sound
Sound
Sound is a mechanical wave that is an oscillation of pressure transmitted through a solid, liquid, or gas, composed of frequencies within the range of hearing and of a level sufficiently strong to be heard, or the sensation stimulated in organs of hearing by such vibrations.-Propagation of...
waves — the velocity v has zero divergence
Divergence
In vector calculus, divergence is a vector operator that measures the magnitude of a vector field's source or sink at a given point, in terms of a signed scalar. More technically, the divergence represents the volume density of the outward flux of a vector field from an infinitesimal volume around...
:
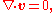
with the dot denoting the inner product. As a result, the velocity potential φ has to satisfy Laplace's equation
Laplace's equation
In mathematics, Laplace's equation is a second-order partial differential equation named after Pierre-Simon Laplace who first studied its properties. This is often written as:where ∆ = ∇² is the Laplace operator and \varphi is a scalar function...
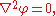
where
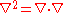 is the Laplace operator
is the Laplace operatorLaplace operator
In mathematics the Laplace operator or Laplacian is a differential operator given by the divergence of the gradient of a function on Euclidean space. It is usually denoted by the symbols ∇·∇, ∇2 or Δ...
(sometimes also written
 ). In this case the flow can be determined completely from its kinematics
). In this case the flow can be determined completely from its kinematicsKinematics
Kinematics is the branch of classical mechanics that describes the motion of bodies and systems without consideration of the forces that cause the motion....
: the assumptions of irrotationality and zero divergence of the flow. Dynamics only have to be applied afterwards, if one is interested in computing pressures: for instance for flow around airfoils through the use of Bernoulli's principle
Bernoulli's principle
In fluid dynamics, Bernoulli's principle states that for an inviscid flow, an increase in the speed of the fluid occurs simultaneously with a decrease in pressure or a decrease in the fluid's potential energy...
.
In two dimensions, potential flow reduces to a very simple system that is analyzed using complex analysis
Complex analysis
Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is useful in many branches of mathematics, including number theory and applied mathematics; as well as in physics,...
(see below).
Steady flow
Potential flow theory can also be used to model irrotational compressible flow. The full potential equation, describing a steady flow, is given by: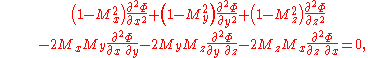
with Mach number
Mach number
Mach number is the speed of an object moving through air, or any other fluid substance, divided by the speed of sound as it is in that substance for its particular physical conditions, including those of temperature and pressure...
components
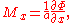
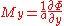 and
and 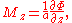
where a is the local speed of sound
Speed of sound
The speed of sound is the distance travelled during a unit of time by a sound wave propagating through an elastic medium. In dry air at , the speed of sound is . This is , or about one kilometer in three seconds or approximately one mile in five seconds....
. The flow velocity v is again equal to ∇Φ, with Φ the velocity potential. The full potential equation is valid for sub-
Speed of sound
The speed of sound is the distance travelled during a unit of time by a sound wave propagating through an elastic medium. In dry air at , the speed of sound is . This is , or about one kilometer in three seconds or approximately one mile in five seconds....
, trans- and supersonic flow at arbitrary angle of attack
Angle of attack
Angle of attack is a term used in fluid dynamics to describe the angle between a reference line on a lifting body and the vector representing the relative motion between the lifting body and the fluid through which it is moving...
, as long as the assumption of irrotationality is applicable.
In case of either subsonic or supersonic (but not transsonic or hypersonic
Hypersonic
In aerodynamics, a hypersonic speed is one that is highly supersonic. Since the 1970s, the term has generally been assumed to refer to speeds of Mach 5 and above...
) flow, at small angles of attack and thin bodies, an additional assumption can be made: the velocity potential is split into an undisturbed onflow velocity V∞ in the x-direction, and small a perturbation
Perturbation theory
Perturbation theory comprises mathematical methods that are used to find an approximate solution to a problem which cannot be solved exactly, by starting from the exact solution of a related problem...
velocity ∇φ thereof. So:

In that case, the linearized small-perturbation potential equation — an approximation to the full potential equation — can be used:
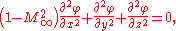
with M∞ = V∞ / a∞ the Mach number of the incoming free stream. This linear equation is much easier to solve than the full potential equation: it may be recast into Laplace's equation by a simple coordinate stretching in the x-direction.
| Derivation of the full potential equation |
|---|
| For a steady inviscid flow, the Euler equations — for the mass and momentum density — are, in subscript notation and in non-conservation form Conservation form Conservation form refers to an arrangement of an equation or system of equations, usually representing a physical system, that show that a property represented is conserved by making overall change equal to zero.... :  while using the summation convention: since j occurs more than once in the term on the left hand side of the momentum equation, j is summed over all its components (which is from j=1 to 2 in two-dimensional flow, and from j=1 to 3 in three dimensions). Further:
The speed of sound squared a2 is equal to the derivative of the pressure p with respect to the density ρ, at constant entropy Entropy Entropy is a thermodynamic property that can be used to determine the energy available for useful work in a thermodynamic process, such as in energy conversion devices, engines, or machines. Such devices can only be driven by convertible energy, and have a theoretical maximum efficiency when... S: 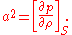 As a result, the flow equations can be written as: 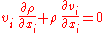 and and  Multiplying (and summing) the momentum equation with vi, and using the mass equation to eliminate the density gradient gives:  When divided by ρ, and with all terms on one side of the equation, the compressible flow equation is:  Note that until this stage, no assumptions have been made regarding the flow (besides that it is a steady flow). Now, for irrotational flow the velocity v is the gradient of the velocity potential Φ, and the local Mach number components Mi are defined as:  and and 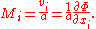 When used in the flow equation, the full potential equation results:  Written out in components, the form given at the beginning of this section is obtained. When a specific equation of state Equation of state In physics and thermodynamics, an equation of state is a relation between state variables. More specifically, an equation of state is a thermodynamic equation describing the state of matter under a given set of physical conditions... is provided, relating pressure p and density ρ, the speed of sound can be determined. Subsequently, together with adequate boundary conditions, the full potential equation can be solved (most often through the use of a computational fluid dynamics Computational fluid dynamics Computational fluid dynamics, usually abbreviated as CFD, is a branch of fluid mechanics that uses numerical methods and algorithms to solve and analyze problems that involve fluid flows. Computers are used to perform the calculations required to simulate the interaction of liquids and gases with... code). |
Sound waves
Small-amplitude sound waves can be approximated with the following potential-flow model: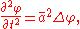
which is a linear wave equation
Wave equation
The wave equation is an important second-order linear partial differential equation for the description of waves – as they occur in physics – such as sound waves, light waves and water waves. It arises in fields like acoustics, electromagnetics, and fluid dynamics...
for the velocity potential φ. Again the oscillatory part of the velocity vector v is related to the velocity potential by v = ∇φ, while as before Δ is the Laplace operator
Laplace operator
In mathematics the Laplace operator or Laplacian is a differential operator given by the divergence of the gradient of a function on Euclidean space. It is usually denoted by the symbols ∇·∇, ∇2 or Δ...
, and ā is the average speed of sound in the homogeneous medium
Transmission medium
A transmission medium is a material substance that can propagate energy waves...
. Note that also the oscillatory parts of the pressure
Pressure
Pressure is the force per unit area applied in a direction perpendicular to the surface of an object. Gauge pressure is the pressure relative to the local atmospheric or ambient pressure.- Definition :...
p and density
Density
The mass density or density of a material is defined as its mass per unit volume. The symbol most often used for density is ρ . In some cases , density is also defined as its weight per unit volume; although, this quantity is more properly called specific weight...
ρ each individually satisfy the wave equation, in this approximation.
Applicability and limitations
Potential flow does not include all the characteristics of flows that are encountered in the real world. For example, potential flow excludes turbulenceTurbulence
In fluid dynamics, turbulence or turbulent flow is a flow regime characterized by chaotic and stochastic property changes. This includes low momentum diffusion, high momentum convection, and rapid variation of pressure and velocity in space and time...
, which is commonly encountered in nature. Also, potential flow theory cannot be applied for viscous internal flow
Internal flow
In fluid mechanics, internal flow is a flow for which the fluid is confined by a surface. Hence the boundary layer is unable to develop without eventually being constrained...
s. Richard Feynman
Richard Feynman
Richard Phillips Feynman was an American physicist known for his work in the path integral formulation of quantum mechanics, the theory of quantum electrodynamics and the physics of the superfluidity of supercooled liquid helium, as well as in particle physics...
considered potential flow to be so unphysical that the only fluid to obey the assumptions was "dry water".
Incompressible potential flow also makes a number of invalid predictions, such as d'Alembert's paradox
D'Alembert's paradox
In fluid dynamics, d'Alembert's paradox is a contradiction reached in 1752 by French mathematician Jean le Rond d'Alembert. D'Alembert proved that – for incompressible and inviscid potential flow – the drag force is zero on a body moving with constant velocity relative to the fluid...
, which states that the drag on any object moving through an infinite fluid otherwise at rest is zero.
More precisely, potential flow cannot account for the behaviour of flows that include a boundary layer
Boundary layer
In physics and fluid mechanics, a boundary layer is that layer of fluid in the immediate vicinity of a bounding surface where effects of viscosity of the fluid are considered in detail. In the Earth's atmosphere, the planetary boundary layer is the air layer near the ground affected by diurnal...
.
Nevertheless, understanding potential flow is important in many branches of fluid mechanics. In particular, simple potential flows (called elementary flows) such as the free vortex and the point source possess ready analytical solutions. These solutions can be superposed
Superposition principle
In physics and systems theory, the superposition principle , also known as superposition property, states that, for all linear systems, the net response at a given place and time caused by two or more stimuli is the sum of the responses which would have been caused by each stimulus individually...
to create more complex flows satisfying a variety of boundary conditions. These flows correspond closely to real-life flows over the whole of fluid mechanics; in addition, many valuable insights arise when considering the deviation (often slight) between an observed flow and the corresponding potential flow.
Potential flow finds many applications in fields such as aircraft design. For instance, in computational fluid dynamics
Computational fluid dynamics
Computational fluid dynamics, usually abbreviated as CFD, is a branch of fluid mechanics that uses numerical methods and algorithms to solve and analyze problems that involve fluid flows. Computers are used to perform the calculations required to simulate the interaction of liquids and gases with...
, one technique is to couple a potential flow solution outside the boundary layer
Boundary layer
In physics and fluid mechanics, a boundary layer is that layer of fluid in the immediate vicinity of a bounding surface where effects of viscosity of the fluid are considered in detail. In the Earth's atmosphere, the planetary boundary layer is the air layer near the ground affected by diurnal...
to a solution of the boundary layer equations inside the boundary layer.
The absence of boundary layer effects means that any streamline can be replaced by a solid boundary with no change in the flow field, a technique used in many aerodynamic design approaches. Another technique would be the use of Riabouchinsky solid
Riabouchinsky solid
In fluid mechanics a Riabouchinsky solid is a technique used for approximating boundary layer separation from a bluff body using potential flow...
s.
Analysis for two-dimensional flow
Potential flow in two dimensions is simple to analyze using conformal mapping, by the use of transformations of the complex planeComplex plane
In mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...
. However,
use of complex numbers is not required, as for example in the classical analysis of fluid flow past a cylinder. It is not possible to solve a potential flow using complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s in three dimensions.
The basic idea is to use a holomorphic (also called analytic
Analytic function
In mathematics, an analytic function is a function that is locally given by a convergent power series. There exist both real analytic functions and complex analytic functions, categories that are similar in some ways, but different in others...
) or meromorphic function f, which maps the physical domain (x,y) to the transformed domain (φ,ψ). While x, y, φ and ψ are all real valued
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
, it is convenient to define the complex quantities
 and
and 
Now, if we write the mapping f as
 or
or 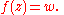
Then, because f is a holomorphic or meromorphic function, it has to satisfy the Cauchy-Riemann equations
Cauchy-Riemann equations
In mathematics, the Cauchy–Riemann differential equations in complex analysis, named after Augustin Cauchy and Bernhard Riemann, consist of a system of two partial differential equations which must be satisfied if we know that a complex function is complex differentiable...
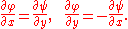
The velocity components (u,v), in the (x,y) directions respectively, can be obtained directly from f by differentiating with respect to z. That is
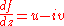
So the velocity field v = (u,v) is specified by
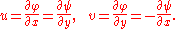
Both φ and ψ then satisfy Laplace's equation
Laplace's equation
In mathematics, Laplace's equation is a second-order partial differential equation named after Pierre-Simon Laplace who first studied its properties. This is often written as:where ∆ = ∇² is the Laplace operator and \varphi is a scalar function...
:
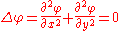 and
and 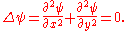
So φ can be identified as the velocity potential and ψ is called the stream function
Stream function
The stream function is defined for two-dimensional flows of various kinds. The stream function can be used to plot streamlines, which represent the trajectories of particles in a steady flow. Streamlines are perpendicular to equipotential lines...
. Lines of constant ψ are known as streamlines and lines of constant φ are known as equipotential lines (see equipotential surface
Equipotential surface
Equipotential surfaces are surfaces of constant scalar potential. They are used to visualize an -dimensional scalar potential function in dimensional space...
).
Streamlines and equipotential lines are orthogonal to each other, since

Thus the flow occurs along the lines of constant ψ and at right angles to the lines of constant φ.
It is interesting to note that Δψ = 0 is also satisfied, this relation being equivalent to ∇×v = 0. So the flow is irrotational. The automatic condition ∂2Ψ /( ∂x ∂y) = ∂2Ψ /( ∂y ∂x) then gives the incompressibility constraint ∇·v = 0.
General considerations
Any differentiable function may be used for . The examples that follow use a variety of elementary functions; special functions may also be used.
. The examples that follow use a variety of elementary functions; special functions may also be used.Note that multi-valued functions such as the natural logarithm
Natural logarithm
The natural logarithm is the logarithm to the base e, where e is an irrational and transcendental constant approximately equal to 2.718281828...
may be used, but attention must be confined to a single Riemann surface
Riemann surface
In mathematics, particularly in complex analysis, a Riemann surface, first studied by and named after Bernhard Riemann, is a one-dimensional complex manifold. Riemann surfaces can be thought of as "deformed versions" of the complex plane: locally near every point they look like patches of the...
.
Power laws
 |
 |
 |
 |
 |
 |
 |
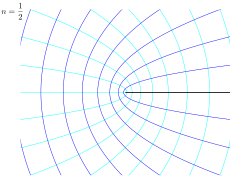
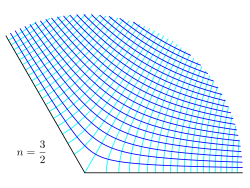
| Examples of conformal maps for the power law w = A zn, for different values of the power n. Shown is the z-plane, showing lines of constant potential φ and streamfunction ψ, while w = φ + iψ. |
In case the following power-law conformal map is applied, from z = x+iy to w = φ+iψ:
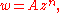
then, writing z in polar coordinates as
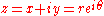 , we have
, we have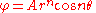 and
and 
In the figures to the right examples are given for several values of n. The black line is the boundary of the flow, while the darker blue lines are streamlines, and the lighter blue lines are equi-potential lines. Some interesting powers n are:
- n = ½ : this corresponds with flow around a semi-infinite plate,
- n = ⅔ : flow around a right corner,
- n = 1 : a trivial case of uniform flow,
- n = 2 : flow through a corner, or near a stagnation point, and
- n = -1 : flow due to a source doublet
The constant A is a scaling parameter: its absolute value
Absolute value
In mathematics, the absolute value |a| of a real number a is the numerical value of a without regard to its sign. So, for example, the absolute value of 3 is 3, and the absolute value of -3 is also 3...
|A| determines the scale, while its argument
Arg (mathematics)
In mathematics, arg is a function operating on complex numbers . It gives the angle between the line joining the point to the origin and the positive real axis, shown as in figure 1 opposite, known as an argument of the point In mathematics, arg is a function operating on complex numbers...
arg{A} introduces a rotation (if non-zero).
Power laws with n = 1: uniform flow
If
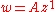 , that is, a power law with
, that is, a power law with  , the streamlines (i.e. lines of constant
, the streamlines (i.e. lines of constant 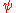 ) are a system of straight lines parallel to the x-axis.
) are a system of straight lines parallel to the x-axis.This is easiest to see by writing in terms of real and imaginary components:

thus giving
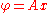 and
and 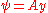 . This flow may be interpreted as uniform flow parallel to the x-axis.
. This flow may be interpreted as uniform flow parallel to the x-axis.Power laws with n = 2
If , then
, then  and the streamline corresponding to a particular value of
and the streamline corresponding to a particular value of 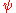 are those points satisfying
are those points satisfying
which is a system of rectangular hyperbolae
Hyperbola
In mathematics a hyperbola is a curve, specifically a smooth curve that lies in a plane, which can be defined either by its geometric properties or by the kinds of equations for which it is the solution set. A hyperbola has two pieces, called connected components or branches, which are mirror...
. This may be seen by again rewriting in terms of real and imaginary components. Noting that
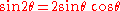 and rewriting
and rewriting 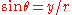 and
and  it is seen (on simplifying) that the streamlines are given by
it is seen (on simplifying) that the streamlines are given by
The velocity field is given by
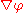 , or
, or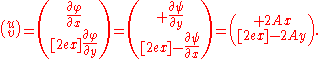
In fluid dynamics, the flowfield near the origin corresponds to a stagnation point
Stagnation point
In fluid dynamics, a stagnation point is a point in a flow field where the local velocity of the fluid is zero. Stagnation points exist at the surface of objects in the flow field, where the fluid is brought to rest by the object...
. Note that the fluid at the origin is at rest (this follows on differentiation of
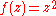 at
at  ).
).The
 streamline is particularly interesting: it has two (or four) branches, following the coordinate axes, i.e.
streamline is particularly interesting: it has two (or four) branches, following the coordinate axes, i.e.  and
and  .
.As no fluid flows across the x-axis, it (the x-axis) may be treated as a solid boundary. It is thus possible to ignore the flow in the lower half-plane where
 and to focus on the flow in the upper half-plane.
and to focus on the flow in the upper half-plane.With this interpretation, the flow is that of a vertically directed jet impinging on a horizontal flat plate.
The flow may also be interpreted as flow into a 90 degree corner if the regions specified by (say)
 and
and  are ignored.
are ignored.Power laws with n = 3
If , the resulting flow is a sort of hexagonal version of the
, the resulting flow is a sort of hexagonal version of the  case considered above. Streamlines are given by,
case considered above. Streamlines are given by, 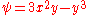 and the flow in this case may be interpreted as flow into a 60 degree corner.
and the flow in this case may be interpreted as flow into a 60 degree corner.Power laws with n = −1: doublet
If
 , the streamlines are given by
, the streamlines are given by
This is more easily interpreted in terms of real and imaginary components:


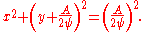
Thus the streamlines are circle
Circle
A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....
s that are tangent to the x-axis at the origin.
The circles in the upper half-plane thus flow clockwise, those in the lower half-plane flow anticlockwise. Note that the velocity components are proportional to
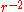 ; and their values at the origin is infinite. This flow pattern is usually referred to as a doublet and can be interpreted as the combination of source-sink pair of infinite strength kept at an infinitesimally small distance apart.
; and their values at the origin is infinite. This flow pattern is usually referred to as a doublet and can be interpreted as the combination of source-sink pair of infinite strength kept at an infinitesimally small distance apart.The velocity field is given by
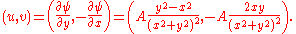
or in polar coordinates:
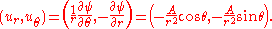
Power laws with n = −2: quadrupole
If , the streamlines are given by
, the streamlines are given by
This is the flow field associated with a quadrupole.
See also
- Stream functionStream functionThe stream function is defined for two-dimensional flows of various kinds. The stream function can be used to plot streamlines, which represent the trajectories of particles in a steady flow. Streamlines are perpendicular to equipotential lines...
- Laplacian field
- Conformal mapping
- FlownetFlownetA flownet is a graphical representation of two-dimensional steady-state groundwater flow through aquifers. Construction of a flownet is often used for solving groundwater flow problems where the geometry makes analytical solutions impractical...
- Velocity potential
- Aerodynamic Potential Flow Codes

