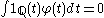Weak derivative
Encyclopedia
In mathematics
, a weak derivative is a generalization of the concept of the derivative
of a function
(strong derivative) for functions not assumed differentiable, but only integrable, i.e. to lie in the Lebesgue space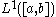
. See distribution
s for an even more general definition.
be a function in the Lebesgue space 
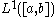. We say that 
in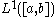 
is a weak derivative of 
if,
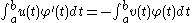
for all infinitely differentiable function
s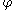
with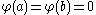 
. This definition is motivated by the integration technique of Integration by parts
.
Generalizing to
dimensions, if 
and 
are in the space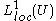 
of locally integrable function
s for some open set
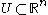, and if 
is a multiindex, we say that 
is the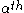 
-weak derivative of 
if
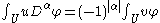
for all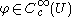
, that is, for all infinitely differentiable functions 
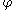with compact support in 
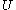. If 
has a weak derivative, it is often written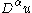 
since weak derivatives are unique (at least, up to a set of measure zero, see below).
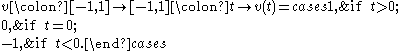
zero, i.e., they are equal almost everywhere
. If we consider equivalence classes of functions, where two functions are equivalent if they are equal almost everywhere, then the weak derivative is unique.
Also, if u is differentiable in the conventional sense then its weak derivative is identical (in the sense given above) to its conventional (strong) derivative. Thus the weak derivative is a generalization of the strong one. Furthermore, the classical rules for derivatives of sums and products of functions also hold for the weak derivative.
s in Sobolev space
s, which are useful for problems of differential equations and in functional analysis
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a weak derivative is a generalization of the concept of the derivative
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
of a function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
(strong derivative) for functions not assumed differentiable, but only integrable, i.e. to lie in the Lebesgue space
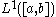. See distributionDistribution (mathematics)
In mathematical analysis, distributions are objects that generalize functions. Distributions make it possible to differentiate functions whose derivatives do not exist in the classical sense. In particular, any locally integrable function has a distributional derivative...
s for an even more general definition.
Definition
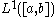Let be a function in the Lebesgue space . We say that in 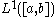is a weak derivative of if,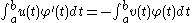for all infinitely differentiable function
Differentiable function
In calculus , a differentiable function is a function whose derivative exists at each point in its domain. The graph of a differentiable function must have a non-vertical tangent line at each point in its domain...
s
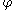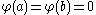with . This definition is motivated by the integration technique of Integration by partsIntegration by parts
In calculus, and more generally in mathematical analysis, integration by parts is a rule that transforms the integral of products of functions into other integrals...
.
Generalizing to
dimensions, if and are in the space 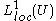of locally integrable functionLocally integrable function
In mathematics, a locally integrable function is a function which is integrable on any compact set of its domain of definition. Their importance lies on the fact that we do not care about their behavior at infinity.- Formal definition :...
s for some open set
Open set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
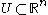, and if is a multiindex, we say that is the 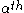-weak derivative of if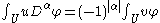for all
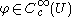, that is, for all infinitely differentiable functions 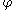with compact support in 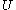. If has a weak derivative, it is often written 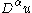since weak derivatives are unique (at least, up to a set of measure zero, see below).Examples
- The absolute valueAbsolute valueIn mathematics, the absolute value |a| of a real number a is the numerical value of a without regard to its sign. So, for example, the absolute value of 3 is 3, and the absolute value of -3 is also 3...
function u : [−1, 1] → [0, 1], u(t) = |t|, which is not differentiable at t = 0, has a weak derivative v known as the sign functionSign functionIn mathematics, the sign function is an odd mathematical function that extracts the sign of a real number. To avoid confusion with the sine function, this function is often called the signum function ....
given by
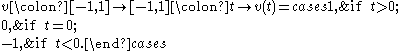
- This is not the only weak derivative for u: any w that is equal to v almost everywhereAlmost everywhereIn measure theory , a property holds almost everywhere if the set of elements for which the property does not hold is a null set, that is, a set of measure zero . In cases where the measure is not complete, it is sufficient that the set is contained within a set of measure zero...
is also a weak derivative for u. Usually, this is not a problem, since in the theory of Lp spacesLp spaceIn mathematics, the Lp spaces are function spaces defined using a natural generalization of the p-norm for finite-dimensional vector spaces...
and Sobolev spaceSobolev spaceIn mathematics, a Sobolev space is a vector space of functions equipped with a norm that is a combination of Lp-norms of the function itself as well as its derivatives up to a given order. The derivatives are understood in a suitable weak sense to make the space complete, thus a Banach space...
s, functions that are equal almost everywhere are identified.
- The characteristic functionCharacteristic functionIn mathematics, characteristic function can refer to any of several distinct concepts:* The most common and universal usage is as a synonym for indicator function, that is the function* In probability theory, the characteristic function of any probability distribution on the real line is given by...
of the rational numbers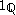
is nowhere differentiable yet has a weak derivative everywhere. Since the Lebesgue measureLebesgue measureIn measure theory, the Lebesgue measure, named after French mathematician Henri Lebesgue, is the standard way of assigning a measure to subsets of n-dimensional Euclidean space. For n = 1, 2, or 3, it coincides with the standard measure of length, area, or volume. In general, it is also called...
of the rational numbers is zero,
- Thus
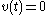is the weak derivative of 
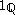. Note that this does agree with our intuition since when considered as a member of an Lp space, 
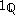is identified with the zero function.
Properties
If two functions are weak derivatives of the same function, they are equal except on a set with Lebesgue measureLebesgue measure
In measure theory, the Lebesgue measure, named after French mathematician Henri Lebesgue, is the standard way of assigning a measure to subsets of n-dimensional Euclidean space. For n = 1, 2, or 3, it coincides with the standard measure of length, area, or volume. In general, it is also called...
zero, i.e., they are equal almost everywhere
Almost everywhere
In measure theory , a property holds almost everywhere if the set of elements for which the property does not hold is a null set, that is, a set of measure zero . In cases where the measure is not complete, it is sufficient that the set is contained within a set of measure zero...
. If we consider equivalence classes of functions, where two functions are equivalent if they are equal almost everywhere, then the weak derivative is unique.
Also, if u is differentiable in the conventional sense then its weak derivative is identical (in the sense given above) to its conventional (strong) derivative. Thus the weak derivative is a generalization of the strong one. Furthermore, the classical rules for derivatives of sums and products of functions also hold for the weak derivative.
Extensions
This concept gives rise to the definition weak solutionWeak solution
In mathematics, a weak solution to an ordinary or partial differential equation is a function for which the derivatives may not all exist but which is nonetheless deemed to satisfy the equation in some precisely defined sense. There are many different definitions of weak solution, appropriate for...
s in Sobolev space
Sobolev space
In mathematics, a Sobolev space is a vector space of functions equipped with a norm that is a combination of Lp-norms of the function itself as well as its derivatives up to a given order. The derivatives are understood in a suitable weak sense to make the space complete, thus a Banach space...
s, which are useful for problems of differential equations and in functional analysis
Functional analysis
Functional analysis is a branch of mathematical analysis, the core of which is formed by the study of vector spaces endowed with some kind of limit-related structure and the linear operators acting upon these spaces and respecting these structures in a suitable sense...
.