
Integrable system
Encyclopedia
In mathematics
and physics
, there are various distinct notions that are referred to under the name of integrable systems.
In the general theory of differential systems, there is Frobenius integrability, which refers to overdetermined systems. In the classical theory of Hamiltonian dynamical systems, there is the notion of Liouville integrability. More generally, in differentiable dynamical systems integrability relates to the existence of foliation
s by invariant submanifolds within the phase space
. Each of these notions involves an application of the idea of foliations, but they do not coincide. There are also notions of complete integrability, or exact solvability in the setting of quantum systems and statistical mechanical models.
sense if the space on which it is defined has a foliation
by maximal integral manifolds. The Frobenius theorem
states that a system is completely integrable if and only if it generates an ideal that is closed under exterior differentation
. (See the article on integrability conditions for differential systems
for a detailed discussion of foliations by maximal integral manifolds.)
. There is thus a variable notion of the degree of integrability, depending on the dimension of the leaves of the invariant foliation.
This concept has a refinement in the case of Hamiltonian systems
, known as complete integrability in the sense of Liouville (see below), which is what is most frequently referred to in this context.
An extension of the notion of integrability is also applicable to discrete systems such as lattices.
This definition can be adapted to describe evolution equations that either are systems of
differential equations or finite difference equations
.
The distinction between integrable and nonintegrable dynamical systems thus has the qualitative
implication of regular motion vs. chaotic motion and hence is an intrinsic property, not just a matter of whether
a system can be explicitly integrated in exact form.
Liouville integrability means that there exists a regular foliation of the phase space by invariant manifolds such that the Hamiltonian vector fields
associated to the invariants of the foliation span the tangent distribution. Another way to state this is that there exists
a maximal set of Poisson commuting invariants (i.e., functions on the phase space whose Poisson bracket
s with the Hamiltonian of the system,
and with each other, vanish).
In finite dimensions, if the phase space
is symplectic (i.e., the center of the Poisson algebra consists only of constants), then it must have
even dimension , and the maximal number of independent Poisson commuting invariants (including the Hamiltonian itself) is
, and the maximal number of independent Poisson commuting invariants (including the Hamiltonian itself) is
 . The leaves of the foliation are totally isotropic with respect to the symplectic form and such a maximal isotropic foliation is
. The leaves of the foliation are totally isotropic with respect to the symplectic form and such a maximal isotropic foliation is
called Lagrangian
. All autonomous Hamiltonian systems (i.e. those for which the Hamiltonian and Poisson brackets are not explicitly time dependent)
have at least one invariant; namely, the Hamiltonian itself, whose value along the flow is the energy. If the energy level sets are compact, the
leaves of the Lagrangian foliation are tori, and the natural linear coordinates on these are called "angle" variables. The cycles of the canonical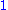 -form
-form
are called the action variables, and the resulting canonical coordinates are called action-angle variables (see below).
There is also a distinction between complete integrability, in the Liouville sense, and partial integrability, as well as
a notion of superintegrability
and maximal superintegrability. Essentially, these distinctions correspond to the dimensions of the leaves of the foliation.
When the number of independent Poisson commuting invariants is less than maximal (but, in the case of
autonomous systems, more than one), we say the system is partially integrable.
When there exist further functionally independent invariants, beyond the maximal number that
can be Poisson commuting, and hence the dimension of the leaves of the invariant foliation is
less than n, we say the system is superintegrable. If there is a regular foliation with one-dimensional
leaves (curves), this is called maximally superintegrable.
and the energy level sets are compact, the flows are complete, and the leaves of the invariant foliation are tori
.
There then exist, as mentioned above, special sets of canonical coordinates
on the phase space
known as action-angle variables,
such that the invariant tori are the joint level sets of the action
variables. These thus provide a complete set of invariants
of the Hamiltonian flow (constants of motion), and the angle variables are the natural periodic coordinates on the torus. The motion on the
invariant tori, expressed in terms of these canonical coordinates, is linear in the angle variables.
theory, there is the Hamilton–Jacobi method, in which solutions to Hamilton's equations are sought by first finding a complete solution of the associated Hamilton–Jacobi equation. In classical terminology, this is described as determining a transformation to a canonical set of coordinates consisting of completely ignorable variables; i.e., those in which there is no dependence of the Hamiltonian on a complete set of canonical "position" coordinates, and hence the corresponding canonically conjugate momenta are all conserved quantities. In the case of compact energy level sets, this is the first step towards determining the action-angle variables. In the general theory of partial differential equations of Hamilton–Jacobi type, a complete solution (i.e. one that depends on n independent constants of integration, where n is the dimension of the configuration space), exists in very general cases, but only in the local sense. Therefore the existence of a complete solution of the Hamilton–Jacobi equation is by no means a characterization of complete integrability in the Liouville sense. Most cases that can be "explicitly integrated" involve a complete separation of variables
, in which the separation constants provide the complete set of integration constants that are required. Only when these constants can be reinterpreted, within the full phase space setting, as the values of a complete set of Poisson commuting functions restricted to the leaves of a Lagrangian foliation, can the system be regarded as completely integrable in the Liouville sense.
s, which are strongly stable, localized solutions of partial differential equations like the Korteweg–de Vries equation
(which describes 1-dimensional non-dissipative fluid dynamics in shallow basins), could be understood by viewing these equations as infinite dimensional integrable
Hamiltonian systems. Their study leads to a very fruitful approach for "integrating" such systems, the inverse scattering transform
and more general inverse spectral methods (often reducible to Riemann–Hilbert problems),
which generalize local linear methods like Fourier analysis to nonlocal linearization, through the solution of associated integral equations.
The basic idea of this method is to introduce a linear operator that is determined by the position in phase space and which evolves under the dynamics of the system in question in such a way that its "spectrum" (in a suitably generalized sense) is invariant under the evolution. This provides, in certain cases, enough invariants, or "integrals of motion" to make the system completely integrable. In the case of systems having an infinite number of degrees of freedom, such as the KdV equation, this is not sufficient to make precise the property of Liouville integrability. However, for suitably defined boundary conditions, the spectral transform can, in fact, be interpreted as a transformation to completely ignorable coordinates, in which the conserved quantities form half of a doubly infinite set of canonical coordinates, and the flow linearizes in these. In some cases, this may even be seen as a transformation to action-angle variables, although typically only a finite number of the "position" variables are actually angle coordinates, and the rest are noncompact.
In the quantum setting, functions on phase space must be replaced by self-adjoint operators on a Hilbert space
, and the notion
of Poisson commuting functions replaced by commuting operators.
Since there is no clear definition of independence of operators, except for
special classes, the definition of integrable system, in the quantum sense, is not yet agreed upon. The working definition
that is mostly used is that there is a maximal set of commuting operators, including the Hamiltonian, and a semiclassical
limit in which these operators have symbols that are independent Poisson commuting functions on the phase space.
Quantum integrable systems can be explicitly solved by Bethe Ansatz
or Quantum inverse scattering method
. Examples are Lieb-Liniger Model
, Hubbard model
and Heisenberg model (quantum)
.
This obscures the distinction between integrability in the Hamiltonian sense, and the more general dynamical systems sense.
There are also exactly solvable models in statistical mechanics, which are more closely
related to quantum integrable systems than classical ones. Two closely related methods: the Bethe ansatz
approach, in its modern sense, based on the Yang-Baxter equation
s and the Quantum inverse scattering method
provide quantum analogs of the Inverse Spectral methods. These are equally important in the study of
solvable models in statistical mechanics.
An imprecise notion of "exact solvability" as meaning: "The solutions can be expressed explicitly in terms
of some previously known functions" is also sometimes used, as though this were an intrinsic
property of the system itself, rather than the purely calculational feature that we happen to have
some "known" functions available, in terms of which the solutions may be expressed.
This notion has no intrinsic meaning, since what is meant by "known" functions very often is defined precisely
by the fact that they satisfy certain given equations, and the list of such "known functions"
is constantly growing. Although such a characterization of "integrability" has no intrinsic validity,
it often implies the sort of regularity that is to be expected in integrable systems.
2. Integrable lattice models
3. Integrable systems of PDEs in 1 + 1 dimension
4. Integrable PDEs in 2 + 1 dimensions
5. Other integrable systems of PDEs in higher dimensions
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
and physics
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
, there are various distinct notions that are referred to under the name of integrable systems.
In the general theory of differential systems, there is Frobenius integrability, which refers to overdetermined systems. In the classical theory of Hamiltonian dynamical systems, there is the notion of Liouville integrability. More generally, in differentiable dynamical systems integrability relates to the existence of foliation
Foliation
In mathematics, a foliation is a geometric device used to study manifolds, consisting of an integrable subbundle of the tangent bundle. A foliation looks locally like a decomposition of the manifold as a union of parallel submanifolds of smaller dimension....
s by invariant submanifolds within the phase space
Phase space
In mathematics and physics, a phase space, introduced by Willard Gibbs in 1901, is a space in which all possible states of a system are represented, with each possible state of the system corresponding to one unique point in the phase space...
. Each of these notions involves an application of the idea of foliations, but they do not coincide. There are also notions of complete integrability, or exact solvability in the setting of quantum systems and statistical mechanical models.
Frobenius Integrability (overdetermined differential systems)
A differential system is said to be completely integrable in the FrobeniusFerdinand Georg Frobenius
Ferdinand Georg Frobenius was a German mathematician, best known for his contributions to the theory of differential equations and to group theory...
sense if the space on which it is defined has a foliation
Foliation
In mathematics, a foliation is a geometric device used to study manifolds, consisting of an integrable subbundle of the tangent bundle. A foliation looks locally like a decomposition of the manifold as a union of parallel submanifolds of smaller dimension....
by maximal integral manifolds. The Frobenius theorem
Frobenius theorem (differential topology)
In mathematics, Frobenius' theorem gives necessary and sufficient conditions for finding a maximal set of independent solutions of an overdetermined system of first-order homogeneous linear partial differential equations...
states that a system is completely integrable if and only if it generates an ideal that is closed under exterior differentation
Exterior derivative
In differential geometry, the exterior derivative extends the concept of the differential of a function, which is a 1-form, to differential forms of higher degree. Its current form was invented by Élie Cartan....
. (See the article on integrability conditions for differential systems
Integrability conditions for differential systems
In mathematics, certain systems of partial differential equations are usefully formulated, from the point of view of their underlying geometric and algebraic structure, in terms of a system of differential forms. The idea is to take advantage of the way a differential form restricts to a...
for a detailed discussion of foliations by maximal integral manifolds.)
General dynamical systems
In the context of differentiable dynamical systems, the notion of integrability refers to the existence of invariant, regular foliations; i.e., ones whose leaves are embedded submanifolds of the smallest possible dimension that are invariant under the flowFlow (mathematics)
In mathematics, a flow formalizes the idea of the motion of particles in a fluid. Flows are ubiquitous in science, including engineering and physics. The notion of flow is basic to the study of ordinary differential equations. Informally, a flow may be viewed as a continuous motion of points over...
. There is thus a variable notion of the degree of integrability, depending on the dimension of the leaves of the invariant foliation.
This concept has a refinement in the case of Hamiltonian systems
Hamiltonian mechanics
Hamiltonian mechanics is a reformulation of classical mechanics that was introduced in 1833 by Irish mathematician William Rowan Hamilton.It arose from Lagrangian mechanics, a previous reformulation of classical mechanics introduced by Joseph Louis Lagrange in 1788, but can be formulated without...
, known as complete integrability in the sense of Liouville (see below), which is what is most frequently referred to in this context.
An extension of the notion of integrability is also applicable to discrete systems such as lattices.
This definition can be adapted to describe evolution equations that either are systems of
differential equations or finite difference equations
Finite difference
A finite difference is a mathematical expression of the form f − f. If a finite difference is divided by b − a, one gets a difference quotient...
.
The distinction between integrable and nonintegrable dynamical systems thus has the qualitative
implication of regular motion vs. chaotic motion and hence is an intrinsic property, not just a matter of whether
a system can be explicitly integrated in exact form.
Hamiltonian systems and Liouville integrability
In the special setting of Hamiltonian systems, we have the notion of integrability in the Liouville sense.Liouville integrability means that there exists a regular foliation of the phase space by invariant manifolds such that the Hamiltonian vector fields
associated to the invariants of the foliation span the tangent distribution. Another way to state this is that there exists
a maximal set of Poisson commuting invariants (i.e., functions on the phase space whose Poisson bracket
Poisson bracket
In mathematics and classical mechanics, the Poisson bracket is an important binary operation in Hamiltonian mechanics, playing a central role in Hamilton's equations of motion, which govern the time-evolution of a Hamiltonian dynamical system...
s with the Hamiltonian of the system,
and with each other, vanish).
In finite dimensions, if the phase space
Phase space
In mathematics and physics, a phase space, introduced by Willard Gibbs in 1901, is a space in which all possible states of a system are represented, with each possible state of the system corresponding to one unique point in the phase space...
is symplectic (i.e., the center of the Poisson algebra consists only of constants), then it must have
even dimension
 , and the maximal number of independent Poisson commuting invariants (including the Hamiltonian itself) is
, and the maximal number of independent Poisson commuting invariants (including the Hamiltonian itself) is . The leaves of the foliation are totally isotropic with respect to the symplectic form and such a maximal isotropic foliation is
. The leaves of the foliation are totally isotropic with respect to the symplectic form and such a maximal isotropic foliation iscalled Lagrangian
Joseph Louis Lagrange
Joseph-Louis Lagrange , born Giuseppe Lodovico Lagrangia, was a mathematician and astronomer, who was born in Turin, Piedmont, lived part of his life in Prussia and part in France, making significant contributions to all fields of analysis, to number theory, and to classical and celestial mechanics...
. All autonomous Hamiltonian systems (i.e. those for which the Hamiltonian and Poisson brackets are not explicitly time dependent)
have at least one invariant; namely, the Hamiltonian itself, whose value along the flow is the energy. If the energy level sets are compact, the
leaves of the Lagrangian foliation are tori, and the natural linear coordinates on these are called "angle" variables. The cycles of the canonical
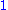 -form
-formare called the action variables, and the resulting canonical coordinates are called action-angle variables (see below).
There is also a distinction between complete integrability, in the Liouville sense, and partial integrability, as well as
a notion of superintegrability
Superintegrable Hamiltonian system
In mathematics, a superintegrable Hamiltonian system is a Hamiltonian system on a 2n-dimensional symplectic manifold for which the following conditions hold: There exist n ≤ k independent integrals F i of motion...
and maximal superintegrability. Essentially, these distinctions correspond to the dimensions of the leaves of the foliation.
When the number of independent Poisson commuting invariants is less than maximal (but, in the case of
autonomous systems, more than one), we say the system is partially integrable.
When there exist further functionally independent invariants, beyond the maximal number that
can be Poisson commuting, and hence the dimension of the leaves of the invariant foliation is
less than n, we say the system is superintegrable. If there is a regular foliation with one-dimensional
leaves (curves), this is called maximally superintegrable.
Action-angle variables
When a finite dimensional Hamiltonian system is completely integrable in the Liouville sense,and the energy level sets are compact, the flows are complete, and the leaves of the invariant foliation are tori
Torus
In geometry, a torus is a surface of revolution generated by revolving a circle in three dimensional space about an axis coplanar with the circle...
.
There then exist, as mentioned above, special sets of canonical coordinates
Canonical coordinates
In mathematics and classical mechanics, canonical coordinates are particular sets of coordinates on the phase space, or equivalently, on the cotangent manifold of a manifold. Canonical coordinates arise naturally in physics in the study of Hamiltonian mechanics...
on the phase space
Phase space
In mathematics and physics, a phase space, introduced by Willard Gibbs in 1901, is a space in which all possible states of a system are represented, with each possible state of the system corresponding to one unique point in the phase space...
known as action-angle variables,
such that the invariant tori are the joint level sets of the action
Action (physics)
In physics, action is an attribute of the dynamics of a physical system. It is a mathematical functional which takes the trajectory, also called path or history, of the system as its argument and has a real number as its result. Action has the dimension of energy × time, and its unit is...
variables. These thus provide a complete set of invariants
of the Hamiltonian flow (constants of motion), and the angle variables are the natural periodic coordinates on the torus. The motion on the
invariant tori, expressed in terms of these canonical coordinates, is linear in the angle variables.
The Hamilton–Jacobi approach
In canonical transformationCanonical transformation
In Hamiltonian mechanics, a canonical transformation is a change of canonical coordinates → that preserves the form of Hamilton's equations , although it...
theory, there is the Hamilton–Jacobi method, in which solutions to Hamilton's equations are sought by first finding a complete solution of the associated Hamilton–Jacobi equation. In classical terminology, this is described as determining a transformation to a canonical set of coordinates consisting of completely ignorable variables; i.e., those in which there is no dependence of the Hamiltonian on a complete set of canonical "position" coordinates, and hence the corresponding canonically conjugate momenta are all conserved quantities. In the case of compact energy level sets, this is the first step towards determining the action-angle variables. In the general theory of partial differential equations of Hamilton–Jacobi type, a complete solution (i.e. one that depends on n independent constants of integration, where n is the dimension of the configuration space), exists in very general cases, but only in the local sense. Therefore the existence of a complete solution of the Hamilton–Jacobi equation is by no means a characterization of complete integrability in the Liouville sense. Most cases that can be "explicitly integrated" involve a complete separation of variables
Separation of variables
In mathematics, separation of variables is any of several methods for solving ordinary and partial differential equations, in which algebra allows one to rewrite an equation so that each of two variables occurs on a different side of the equation....
, in which the separation constants provide the complete set of integration constants that are required. Only when these constants can be reinterpreted, within the full phase space setting, as the values of a complete set of Poisson commuting functions restricted to the leaves of a Lagrangian foliation, can the system be regarded as completely integrable in the Liouville sense.
Solitons and inverse spectral methods
A resurgence of interest in classical integrable systems came with the discovery, in the late 1960s, that solitonSoliton
In mathematics and physics, a soliton is a self-reinforcing solitary wave that maintains its shape while it travels at constant speed. Solitons are caused by a cancellation of nonlinear and dispersive effects in the medium...
s, which are strongly stable, localized solutions of partial differential equations like the Korteweg–de Vries equation
Korteweg–de Vries equation
In mathematics, the Korteweg–de Vries equation is a mathematical model of waves on shallow water surfaces. It is particularly notable as the prototypical example of an exactly solvable model, that is, a non-linear partial differential equation whose solutions can be exactly and precisely specified...
(which describes 1-dimensional non-dissipative fluid dynamics in shallow basins), could be understood by viewing these equations as infinite dimensional integrable
Hamiltonian systems. Their study leads to a very fruitful approach for "integrating" such systems, the inverse scattering transform
Inverse scattering transform
In mathematics, the inverse scattering transform is a method for solving some non-linear partial differential equations. It is one of the most important developments in mathematical physics in the past 40 years...
and more general inverse spectral methods (often reducible to Riemann–Hilbert problems),
which generalize local linear methods like Fourier analysis to nonlocal linearization, through the solution of associated integral equations.
The basic idea of this method is to introduce a linear operator that is determined by the position in phase space and which evolves under the dynamics of the system in question in such a way that its "spectrum" (in a suitably generalized sense) is invariant under the evolution. This provides, in certain cases, enough invariants, or "integrals of motion" to make the system completely integrable. In the case of systems having an infinite number of degrees of freedom, such as the KdV equation, this is not sufficient to make precise the property of Liouville integrability. However, for suitably defined boundary conditions, the spectral transform can, in fact, be interpreted as a transformation to completely ignorable coordinates, in which the conserved quantities form half of a doubly infinite set of canonical coordinates, and the flow linearizes in these. In some cases, this may even be seen as a transformation to action-angle variables, although typically only a finite number of the "position" variables are actually angle coordinates, and the rest are noncompact.
Quantum integrable systems
There is also a notion of quantum integrable systems.In the quantum setting, functions on phase space must be replaced by self-adjoint operators on a Hilbert space
Hilbert space
The mathematical concept of a Hilbert space, named after David Hilbert, generalizes the notion of Euclidean space. It extends the methods of vector algebra and calculus from the two-dimensional Euclidean plane and three-dimensional space to spaces with any finite or infinite number of dimensions...
, and the notion
of Poisson commuting functions replaced by commuting operators.
Since there is no clear definition of independence of operators, except for
special classes, the definition of integrable system, in the quantum sense, is not yet agreed upon. The working definition
that is mostly used is that there is a maximal set of commuting operators, including the Hamiltonian, and a semiclassical
limit in which these operators have symbols that are independent Poisson commuting functions on the phase space.
Quantum integrable systems can be explicitly solved by Bethe Ansatz
Bethe ansatz
In physics, the Bethe ansatz is a method for finding the exact solutions of certain one-dimensional quantum many-body models. It was invented by Hans Bethe in 1931 to find the exact eigenvalues and eigenvectors of the one-dimensional antiferromagnetic Heisenberg model Hamiltonian...
or Quantum inverse scattering method
Quantum inverse scattering method
Quantum inverse scattering method relates two different approaches:1) Inverse scattering transform is a method of solving classical integrable differential equations of evolutionary type.Important concept is Lax representation....
. Examples are Lieb-Liniger Model
Lieb-Liniger Model
The Lieb–Liniger model describes a gas of particles moving in one dimension and satisfying Bose–Einstein statistics.-Introduction:A model of a gas of particles moving in one dimension and satisfying...
, Hubbard model
Hubbard model
The Hubbard model is an approximate model used, especially in solid state physics, to describe the transition between conducting and insulating systems...
and Heisenberg model (quantum)
Heisenberg model (quantum)
The Heisenberg model is a statistical mechanical model used in the study of critical points and phase transitions of magnetic systems, in which the spin of the magnetic systems are treated quantum mechanically...
.
Exactly solvable models
In physics, completely integrable systems, especially in the infinite dimensional setting, are often referred to as exactly solvable models.This obscures the distinction between integrability in the Hamiltonian sense, and the more general dynamical systems sense.
There are also exactly solvable models in statistical mechanics, which are more closely
related to quantum integrable systems than classical ones. Two closely related methods: the Bethe ansatz
Bethe ansatz
In physics, the Bethe ansatz is a method for finding the exact solutions of certain one-dimensional quantum many-body models. It was invented by Hans Bethe in 1931 to find the exact eigenvalues and eigenvectors of the one-dimensional antiferromagnetic Heisenberg model Hamiltonian...
approach, in its modern sense, based on the Yang-Baxter equation
Yang-Baxter equation
The Yang–Baxter equation is an equation which was first introduced in the field of statistical mechanics. It takes its name from independent work of C. N. Yang from 1968, and R. J. Baxter from 1971...
s and the Quantum inverse scattering method
Quantum inverse scattering method
Quantum inverse scattering method relates two different approaches:1) Inverse scattering transform is a method of solving classical integrable differential equations of evolutionary type.Important concept is Lax representation....
provide quantum analogs of the Inverse Spectral methods. These are equally important in the study of
solvable models in statistical mechanics.
An imprecise notion of "exact solvability" as meaning: "The solutions can be expressed explicitly in terms
of some previously known functions" is also sometimes used, as though this were an intrinsic
property of the system itself, rather than the purely calculational feature that we happen to have
some "known" functions available, in terms of which the solutions may be expressed.
This notion has no intrinsic meaning, since what is meant by "known" functions very often is defined precisely
by the fact that they satisfy certain given equations, and the list of such "known functions"
is constantly growing. Although such a characterization of "integrability" has no intrinsic validity,
it often implies the sort of regularity that is to be expected in integrable systems.
List of some well-known classical integrable systems
1. Classical mechanical systems (finite dimensional phase space):- Harmonic oscillatorHarmonic oscillatorIn classical mechanics, a harmonic oscillator is a system that, when displaced from its equilibrium position, experiences a restoring force, F, proportional to the displacement, x: \vec F = -k \vec x \, where k is a positive constant....
s in n dimensions - Central force motion
- Two center Newtonian gravitational motion
- Geodesic motion on ellipsoids
- Neumann oscillator
- Lagrange, Euler and Kovalevskaya topsLagrange, Euler and Kovalevskaya topsIn classical mechanics, the precession of a top under the influence of gravity is not in general, an integrable problem. There are however three famous cases that are integrable, the Euler, the Lagrange and the Kovalevskaya tops...
- Integrable Clebsch and Steklov systems in fluids
- Calogero–Moser–Sutherland models
- Swinging Atwood's MachineSwinging Atwood's machineThe swinging Atwood's machine is a mechanism that resembles a simple Atwood's machine except that one of the masses is allowed to swing in a two-dimensional plane, producing a dynamical system that is chaotic for some system parameters and initial conditions.Specifically, it comprises two masses ...
with certain choices of parameters
2. Integrable lattice models
- Toda lattice
- Ablowitz–Ladik lattice
- Volterra lattice
3. Integrable systems of PDEs in 1 + 1 dimension
- Korteweg–de Vries equationKorteweg–de Vries equationIn mathematics, the Korteweg–de Vries equation is a mathematical model of waves on shallow water surfaces. It is particularly notable as the prototypical example of an exactly solvable model, that is, a non-linear partial differential equation whose solutions can be exactly and precisely specified...
- Sine–Gordon equation
- Nonlinear Schrodinger equationNonlinear Schrödinger equationIn theoretical physics, the nonlinear Schrödinger equation is a nonlinear version of Schrödinger's equation. It is a classical field equation with applications to optics and water waves. Unlike the Schrödinger equation, it never describes the time evolution of a quantum state...
- Boussinesq equation
- Nonlinear sigma models
- Classical Heisenberg ferromagnet model (spin chain)
- Classical Gaudin spin system (Garnier system)
- Landau–Lifshitz equation (continuous spin field)
- Benjamin–Ono equation
- Dym equation
- Three wave equation
4. Integrable PDEs in 2 + 1 dimensions
- Kadomtsev–Petviashvili equation
- Davey–Stewartson equation
- Ishimori equationIshimori equationThe Ishimori equation is a partial differential equation proposed by the Japanese mathematician . Its interest is as the first example of a nonlinear spin-one field model in the plane that is integrable .-Equation:The IE has the form...
5. Other integrable systems of PDEs in higher dimensions
- Self-dual Yang–Mills equations

