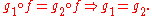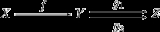
Epimorphism
Encyclopedia
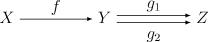
Category theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
, an epimorphism (also called an epic morphism or, colloquially, an epi) is a morphism
Morphism
In mathematics, a morphism is an abstraction derived from structure-preserving mappings between two mathematical structures. The notion of morphism recurs in much of contemporary mathematics...
f : X → Y which is right-cancellative
Cancellation property
In mathematics, the notion of cancellative is a generalization of the notion of invertible.An element a in a magma has the left cancellation property if for all b and c in M, a * b = a * c always implies b = c.An element a in a magma has the right cancellation...
in the sense that, for all morphisms ,
Epimorphisms are analogues of surjective function
Surjective function
In mathematics, a function f from a set X to a set Y is surjective , or a surjection, if every element y in Y has a corresponding element x in X so that f = y...
s, but they are not exactly the same. The dual
Dual (category theory)
In category theory, a branch of mathematics, duality is a correspondence between properties of a category C and so-called dual properties of the opposite category Cop...
of an epimorphism is a monomorphism
Monomorphism
In the context of abstract algebra or universal algebra, a monomorphism is an injective homomorphism. A monomorphism from X to Y is often denoted with the notation X \hookrightarrow Y....
(i.e. an epimorphism in a category C is a monomorphism in the dual category Cop).
Many authors in abstract algebra
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
and universal algebra
Universal algebra
Universal algebra is the field of mathematics that studies algebraic structures themselves, not examples of algebraic structures....
define an epimorphism simply as an onto or surjective homomorphism
Homomorphism
In abstract algebra, a homomorphism is a structure-preserving map between two algebraic structures . The word homomorphism comes from the Greek language: ὁμός meaning "same" and μορφή meaning "shape".- Definition :The definition of homomorphism depends on the type of algebraic structure under...
. Every epimorphism in this algebraic sense is an epimorphism in the sense of category theory, but the converse is not true in all categories. In this article, the term "epimorphism" will be used in the sense of category theory given above. For more on this, see the section on Terminology below.
Examples
Every morphism in a concrete categoryConcrete category
In mathematics, a concrete category is a category that is equipped with a faithful functor to the category of sets. This functor makes it possible to think of the objects of the category as sets with additional structure, and of its morphisms as structure-preserving functions...
whose underlying function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
is surjective is an epimorphism. In many concrete categories of interest the converse is also true. For example, in the following categories, the epimorphisms are exactly those morphisms which are surjective on the underlying sets:
- SetCategory of setsIn the mathematical field of category theory, the category of sets, denoted as Set, is the category whose objects are sets. The arrows or morphisms between sets A and B are all functions from A to B...
, sets and functions. To prove that every epimorphism f: X → Y in Set is surjective, we compose it with both the characteristic function g1: Y → {0,1} of the image f(X) and the map g2: Y → {0,1} that is constant 1. - Rel, sets with binary relationBinary relationIn mathematics, a binary relation on a set A is a collection of ordered pairs of elements of A. In other words, it is a subset of the Cartesian product A2 = . More generally, a binary relation between two sets A and B is a subset of...
s and relation preserving functions. Here we can use the same proof as for Set, equipping {0,1} with the full relation {0,1}×{0,1}. - Pos, partially ordered setPartially ordered setIn mathematics, especially order theory, a partially ordered set formalizes and generalizes the intuitive concept of an ordering, sequencing, or arrangement of the elements of a set. A poset consists of a set together with a binary relation that indicates that, for certain pairs of elements in the...
s and monotone functions. If f : (X,≤) → (Y,≤) is not surjective, pick y0 in Y \ f(X) and let g1 : Y → {0,1} be the characteristic function of {y | y0 ≤ y} and g2 : Y → {0,1} the characteristic function of {y | y0 < y}. These maps are monotone if {0,1} is given the standard ordering 0 < 1. - GrpCategory of groupsIn mathematics, the category Grp has the class of all groups for objects and group homomorphisms for morphisms. As such, it is a concrete category...
, groupsGroup (mathematics)In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
and group homomorphismGroup homomorphismIn mathematics, given two groups and , a group homomorphism from to is a function h : G → H such that for all u and v in G it holds that h = h \cdot h...
s. The result that every epimorphism in Grp is surjective is due to Otto SchreierOtto SchreierOtto Schreier was an Austrian mathematician who made major contributions in combinatorial group theory and in the topology of Lie groups. He studied mathematics at the University of Vienna and obtained his doctorate in 1923, under the supervision of Philipp Furtwängler...
(he actually proved more, showing that every subgroup is an equalizer using the free productFree productIn mathematics, specifically group theory, the free product is an operation that takes two groups G and H and constructs a new group G ∗ H. The result contains both G and H as subgroups, is generated by the elements of these subgroups, and is the “most general” group having these properties...
with one amalgamated subgroup); an elementary proof can be found in (Linderholm 1970). - FinGrp, finite groups and group homomorphisms. Also due to Schreier; the proof given in (Linderholm 1970) establishes this case as well.
- AbCategory of abelian groupsIn mathematics, the category Ab has the abelian groups as objects and group homomorphisms as morphisms. This is the prototype of an abelian category....
, abelian groupAbelian groupIn abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
s and group homomorphisms. - K-VectCategory of vector spacesIn mathematics, especially category theory, the category K-Vect has all vector spaces over a fixed field K as objects and K-linear transformations as morphisms...
, vector spaceVector spaceA vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
s over a fieldField (mathematics)In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
K and K-linear transformationsLinear transformationIn mathematics, a linear map, linear mapping, linear transformation, or linear operator is a function between two vector spaces that preserves the operations of vector addition and scalar multiplication. As a result, it always maps straight lines to straight lines or 0...
. - Mod-R, right moduleModule (mathematics)In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
s over a ringRing (mathematics)In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
R and module homomorphisms. This generalizes the two previous examples; to prove that every epimorphism f: X → Y in Mod-R is surjective, we compose it with both the canonical quotient mapQuotient moduleIn abstract algebra, given a module and a submodule, one can construct their quotient module. This construction, described below, is analogous to how one obtains the ring of integers modulo an integer n, see modular arithmetic...
g 1: Y → Y/f(X) and the zero map g2: Y → Y/f(X). - TopCategory of topological spacesIn mathematics, the category of topological spaces, often denoted Top, is the category whose objects are topological spaces and whose morphisms are continuous maps. This is a category because the composition of two continuous maps is again continuous...
, topological spaces and continuous functionContinuous functionIn mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
s. To prove that every epimorphism in Top is surjective, we proceed exactly as in Set, giving {0,1} the indiscrete topologyTrivial topologyIn topology, a topological space with the trivial topology is one where the only open sets are the empty set and the entire space. Such a space is sometimes called an indiscrete space, and its topology sometimes called an indiscrete topology...
which ensures that all considered maps are continuous. - HComp, compactCompact spaceIn mathematics, specifically general topology and metric topology, a compact space is an abstract mathematical space whose topology has the compactness property, which has many important implications not valid in general spaces...
Hausdorff spaceHausdorff spaceIn topology and related branches of mathematics, a Hausdorff space, separated space or T2 space is a topological space in which distinct points have disjoint neighbourhoods. Of the many separation axioms that can be imposed on a topological space, the "Hausdorff condition" is the most frequently...
s and continuous functions. If f: X → Y is not surjective, let y in Y-fX. Since fX is closed, by Urysohn's LemmaUrysohn's lemmaIn topology, Urysohn's lemma is a lemma that states that a topological space is normal if and only if any two disjoint closed subsets can be separated by a function....
there is a continuous function g1:Y → [0,1] such that g1 is 0 on fX and 1 on y. We compose f with both g1 and the zero function g2: Y → [0,1].
However there are also many concrete categories of interest where epimorphisms fail to be surjective. A few examples are:
- In the category of monoids, Mon, the inclusion mapInclusion mapIn mathematics, if A is a subset of B, then the inclusion map is the function i that sends each element, x of A to x, treated as an element of B:i: A\rightarrow B, \qquad i=x....
N → Z is a non-surjective epimorphism. To see this, suppose that g1 and g2 are two distinct maps from Z to some monoid M. Then for some n in Z, g1(n) ≠ g2(n), so g1(-n) ≠ g2(-n). Either n or -n is in N, so the restrictions of g1 and g2 to N are unequal. - In the category of ringsCategory of ringsIn mathematics, the category of rings, denoted by Ring, is the category whose objects are rings and whose morphisms are ring homomorphisms...
, Ring, the inclusion map Z → Q is a non-surjective epimorphism; to see this, note that any ring homomorphismRing homomorphismIn ring theory or abstract algebra, a ring homomorphism is a function between two rings which respects the operations of addition and multiplication....
on Q is determined entirely by its action on Z, similar to the previous example. A similar argument shows that the natural ring homomorphism from any commutative ringCommutative ringIn ring theory, a branch of abstract algebra, a commutative ring is a ring in which the multiplication operation is commutative. The study of commutative rings is called commutative algebra....
R to any one of its localizationsLocalization of a ringIn abstract algebra, localization is a systematic method of adding multiplicative inverses to a ring. Given a ring R and a subset S, one wants to construct some ring R* and ring homomorphism from R to R*, such that the image of S consists of units in R*...
is an epimorphism. - In the category of commutative rings, a finitely generatedFinitely generatedIn mathematics, finitely generated may refer to:* Finitely generated group* Finitely generated monoid* Finitely generated abelian group* Finitely generated module* Finitely generated ideal* Finitely generated algebra* Finitely generated space...
homomorphism of rings f : R → S is an epimorphism if and only if for all prime idealPrime idealIn algebra , a prime ideal is a subset of a ring which shares many important properties of a prime number in the ring of integers...
s P of R, the ideal Q generated by f(P) is either S or is prime, and if Q is not S, the induced map FracField of fractionsIn abstract algebra, the field of fractions or field of quotients of an integral domain is the smallest field in which it can be embedded. The elements of the field of fractions of the integral domain R have the form a/b with a and b in R and b ≠ 0...
(R/P) → Frac(S/Q) is an isomorphismIsomorphismIn abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...
(EGAÉléments de géométrie algébriqueThe Éléments de géométrie algébrique by Alexander Grothendieck , or EGA for short, is a rigorous treatise, in French, on algebraic geometry that was published from 1960 through 1967 by the Institut des Hautes Études Scientifiques...
IV 17.2.6). - In the category of Hausdorff spaceHausdorff spaceIn topology and related branches of mathematics, a Hausdorff space, separated space or T2 space is a topological space in which distinct points have disjoint neighbourhoods. Of the many separation axioms that can be imposed on a topological space, the "Hausdorff condition" is the most frequently...
s, Haus, the epimorphisms are precisely the continuous functions with denseDense setIn topology and related areas of mathematics, a subset A of a topological space X is called dense if any point x in X belongs to A or is a limit point of A...
images. For example, the inclusion map Q → R, is a non-surjective epimorphism.
The above differs from the case of monomorphisms where it is more frequently true that monomorphisms are precisely those whose underlying functions are injective.
As to examples of epimorphisms in non-concrete categories:
- If a monoidMonoidIn abstract algebra, a branch of mathematics, a monoid is an algebraic structure with a single associative binary operation and an identity element. Monoids are studied in semigroup theory as they are naturally semigroups with identity. Monoids occur in several branches of mathematics; for...
or ringRing (mathematics)In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
is considered as a category with a single object (composition of morphisms given by multiplication), then the epimorphisms are precisely the right-cancellable elements. - If a directed graphDirected graphA directed graph or digraph is a pair G= of:* a set V, whose elements are called vertices or nodes,...
is considered as a category (objects are the vertices, morphisms are the paths, composition of morphisms is the concatenation of paths), then every morphism is an epimorphism.
Properties
Every isomorphismIsomorphism
In abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...
is an epimorphism; indeed only a right-sided inverse is needed: if there exists a morphism j : Y → X such that fj = idY, then f is easily seen to be an epimorphism. A map with such a right-sided inverse is called a split epi
Section (category theory)
In category theory, a branch of mathematics, a section is a right inverse of a morphism. Dually, a retraction is a left inverse...
. In a topos
Topos
In mathematics, a topos is a type of category that behaves like the category of sheaves of sets on a topological space...
, a map that is both a monic morphism and an epimorphism is an isomorphism.
The composition of two epimorphisms is again an epimorphism. If the composition fg of two morphisms is an epimorphism, then f must be an epimorphism.
As some of the above examples show, the property of being an epimorphism is not determined by the morphism alone, but also by the category of context. If D is a subcategory
Subcategory
In mathematics, a subcategory of a category C is a category S whose objects are objects in C and whose morphisms are morphisms in C with the same identities and composition of morphisms. Intuitively, a subcategory of C is a category obtained from C by "removing" some of its objects and...
of C, then every morphism in D which is an epimorphism when considered as a morphism in C is also an epimorphism in D; the converse, however, need not hold; the smaller category can (and often will) have more epimorphisms.
As for most concepts in category theory, epimorphisms are preserved under equivalences of categories
Equivalence of categories
In category theory, an abstract branch of mathematics, an equivalence of categories is a relation between two categories that establishes that these categories are "essentially the same". There are numerous examples of categorical equivalences from many areas of mathematics...
: given an equivalence F : C → D, then a morphism f is an epimorphism in the category C if and only if F(f) is an epimorphism in D. A duality between two categories turns epimorphisms into monomorphisms, and vice versa.
The definition of epimorphism may be reformulated to state that f : X → Y is an epimorphism if and only if the induced maps
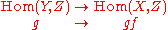
are injective for every choice of Z. This in turn is equivalent to the induced natural transformation
Natural transformation
In category theory, a branch of mathematics, a natural transformation provides a way of transforming one functor into another while respecting the internal structure of the categories involved. Hence, a natural transformation can be considered to be a "morphism of functors". Indeed this intuition...

being a monomorphism in the functor category
Functor category
In category theory, a branch of mathematics, the functors between two given categories form a category, where the objects are the functors and the morphisms are natural transformations between the functors...
SetC.
Every coequalizer
Coequalizer
In category theory, a coequalizer is a generalization of a quotient by an equivalence relation to objects in an arbitrary category...
is an epimorphism, a consequence of the uniqueness requirement in the definition of coequalizers. It follows in particular that every cokernel
Cokernel
In mathematics, the cokernel of a linear mapping of vector spaces f : X → Y is the quotient space Y/im of the codomain of f by the image of f....
is an epimorphism. The converse, namely that every epimorphism be a coequalizer, is not true in all categories.
In many categories it is possible to write every morphism as the composition of a monomorphism followed by an epimorphism. For instance, given a group homomorphism f : G → H, we can define the group K = im(f) = f(G) and then write f as the composition of the surjective homomorphism G → K which is defined like f, followed by the injective homomorphism K → H which sends each element to itself. Such a factorization of an arbitrary morphism into an epimorphism followed by a monomorphism can be carried out in all abelian categories and also in all the concrete categories mentioned above in the Examples section (though not in all concrete categories).
Related concepts
Among other useful concepts are regular epimorphism, extremal epimorphism, strong epimorphism, and split epimorphism. A regular epimorphism coequalizes some parallel pair of morphisms. An extremal epimorphism is an epimorphism that has no monomorphism as a second factor, unless that monomorphism is an isomorphismIsomorphism
In abstract algebra, an isomorphism is a mapping between objects that shows a relationship between two properties or operations. If there exists an isomorphism between two structures, the two structures are said to be isomorphic. In a certain sense, isomorphic structures are...
. A strong epimorphism satisfies a certain lifting property with respect to commutative squares involving a monomorphism.
A split epimorphism is a morphism which has a right-sided inverse.
A morphism that is both a monomorphism and an epimorphism is called a bimorphism. Every isomorphism is a bimorphism but the converse is not true in general. For example, the map from the half-open interval [0,1) to the unit circle
Unit circle
In mathematics, a unit circle is a circle with a radius of one. Frequently, especially in trigonometry, "the" unit circle is the circle of radius one centered at the origin in the Cartesian coordinate system in the Euclidean plane...
S1 (thought of as a subspace of the complex plane
Complex plane
In mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...
) which sends x to exp(2πix) (see Euler's formula
Euler's formula
Euler's formula, named after Leonhard Euler, is a mathematical formula in complex analysis that establishes the deep relationship between the trigonometric functions and the complex exponential function...
) is continuous and bijective but not a homeomorphism
Homeomorphism
In the mathematical field of topology, a homeomorphism or topological isomorphism or bicontinuous function is a continuous function between topological spaces that has a continuous inverse function. Homeomorphisms are the isomorphisms in the category of topological spaces—that is, they are...
since the inverse map is not continuous at 1, so it is an instance of a bimorphism that is not an isomorphism in the category Top. Another example is the embedding Q → R in the category Haus; as noted above, it is a bimorphism, but it is not bijective and therefore not an isomorphism. Similarly, in the category of rings, the maps Z → Q and Q → R are bimorphisms but not isomorphisms.
Epimorphisms are used to define abstract quotient objects in general categories: two epimorphisms f1 : X → Y1 and f2 : X → Y2 are said to be equivalent if there exists an isomorphism j : Y1 → Y2 with j f1 = f2. This is an equivalence relation
Equivalence relation
In mathematics, an equivalence relation is a relation that, loosely speaking, partitions a set so that every element of the set is a member of one and only one cell of the partition. Two elements of the set are considered equivalent if and only if they are elements of the same cell...
, and the equivalence classes are defined to be the quotient objects of X.
Terminology
The companion terms epimorphism and monomorphismMonomorphism
In the context of abstract algebra or universal algebra, a monomorphism is an injective homomorphism. A monomorphism from X to Y is often denoted with the notation X \hookrightarrow Y....
were first introduced by Bourbaki. Bourbaki uses epimorphism as shorthand for a surjective function
Surjective function
In mathematics, a function f from a set X to a set Y is surjective , or a surjection, if every element y in Y has a corresponding element x in X so that f = y...
. Early category theorists believed that epimorphisms were the correct analogue of surjections in an arbitrary category, similar to how monomorphisms are very nearly an exact analogue of injections. Unfortunately this is incorrect; strong or regular epimorphisms behave much more closely to surjections than ordinary epimorphisms. Saunders Mac Lane
Saunders Mac Lane
Saunders Mac Lane was an American mathematician who cofounded category theory with Samuel Eilenberg.-Career:...
attempted to create a distinction between epimorphisms, which were maps in a concrete category whose underlying set maps were surjective, and epic morphisms, which are epimorphisms in the modern sense. However, this distinction never caught on.
It is a common mistake to believe that epimorphisms are either identical to surjections or that they are a better concept. Unfortunately this is rarely the case; epimorphisms can be very mysterious and have unexpected behavior. It is very difficult, for example, to classify all the epimorphisms of rings. In general, epimorphisms are their own unique concept, related to surjections but fundamentally different.