
Topos
Encyclopedia
In mathematics
, a topos (plural "topoi" or "toposes") is a type of category
that behaves like the category of sheaves of sets on a topological space
. For a discussion of the history of topos theory, see the article Background and genesis of topos theory
.
by introducing the notion of a topos. The main utility of this notion is in the abundance of situations in mathematics where topological intuition is very effective but an honest topological space is lacking; it is sometimes possible to find a topos formalizing the intuition. The single greatest success of this programmatic idea to date has been the introduction of the étale topos of a scheme
.
states that the following are equivalent:
A category with these properties is called a "(Grothendieck) topos". Here Presh(D) denotes the category of contravariant functors from D to the category of sets; such a contravariant functor is frequently called a presheaf.
The last axiom needs the most explanation. If X is an object of C, an equivalence relation R on X is a map R→X×X in C
such that all the maps Hom(Y,R)→Hom(Y,X)×Hom(Y,X) are equivalence relations of sets. Since C has colimits we may form the coequalizer of the two maps R→X; call this X/R. The equivalence relation is effective if the canonical map
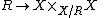
is an isomorphism.
rise to equivalent topoi. As indicated in the introduction, sheaves on ordinary topological spaces motivate many of the basic definitions and results of topos theory.
The category of sets is an important special case: it plays the role of a point in topos theory. Indeed, a set may be thought of as a sheaf on a point.
More exotic examples, and the raison d'être of topos theory, come from algebraic geometry. To a scheme
and even a stack one may associate an étale
topos, an fppf topos, a Nisnevich
topos...
Topos theory is, in some sense, a generalization of classical point-set topology. One should therefore expect to see old and new instances of pathological
behavior. For instance, there is an example due to Pierre Deligne
of a nontrivial topos that has no points (see below).
By Freyd's adjoint functor theorem, to give a geometric morphism X → Y is to give a functor u∗: Y → X that preserves finite limits and all small colimits. Thus geometric morphisms between topoi may be seen as analogues of maps of locales.
If X and Y are topological spaces and u is a continuous map between them, then the pullback and pushforward operations on sheaves yield a geometric morphism between the associated topoi.
If X is an ordinary space and x is a point of X, then the functor that takes a sheaf F to its stalk Fx has a right adjoint
(the "skyscraper sheaf" functor), so an ordinary point of X also determines a topos-theoretic point. These may be constructed as the pullback-pushforward along the continuous map x: 1 → X.
s go through for ringed topoi. The category of R-module objects in X is an abelian category
with enough injectives. A more useful abelian category is the subcategory of quasi-coherent R-modules: these are R-modules that admit a presentation.
Another important class of ringed topoi, besides ringed spaces, are the etale topoi of Deligne-Mumford stacks.
and Barry Mazur
associated to any topos a pro-simplicial set
. Using this inverse system
of simplicial sets one may sometimes associate to a homotopy invariant in classical topology an inverse system
of invariants in topos theory.
The pro-simplicial set associated to the etale topos of a scheme is a pro-finite
simplicial set. Its study is called étale homotopy theory.
, in which all mathematical objects are ultimately represented by sets (even functions
which map between sets). More recent work in category theory
allows this foundation to be generalized using toposes; each topos completely defines its own mathematical framework. The category of sets forms a familiar topos, and working within this topos is equivalent to using traditional set theoretic mathematics. But one could instead choose to work with many alternative toposes. A standard formulation of the axiom of choice makes sense in any topos, and there are toposes in which it is invalid. Constructivists will be interested to work in a topos without the law of excluded middle
. If symmetry under a particular group
G is of importance, one can use the topos consisting of all G-sets
.
It is also possible to encode an algebraic theory
, such as the theory of group
s, as a topos. The individual models of the theory, i.e. the groups in our example, then correspond to functor
s from the encoding topos to the category of sets that respect the topos structure.
A topos is a category
which has the following two properties:
Formally, a power object of an object is a pair
is a pair 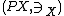 with
with 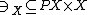 , which classifies relations, in the following sense.
, which classifies relations, in the following sense.
First note that for every object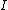 , a morphism
, a morphism 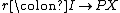 ("a family of subsets") induces a subobject
("a family of subsets") induces a subobject 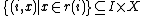 . Formally, this is defined by pulling back
. Formally, this is defined by pulling back 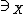 along
along 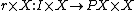 . The universal property of a power object is that every relation arises in this way, giving a bijective correspondence between relations
. The universal property of a power object is that every relation arises in this way, giving a bijective correspondence between relations 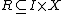 and morphisms
and morphisms 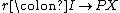 .
.
From finite limits and power objects one can derive that
In some applications, the role of the subobject classifier is pivotal, whereas power objects are not. Thus some definitions reverse the roles of what is defined and what is derived.
for which the notion of subobject of an object has an elementary
or first-order definition. This notion, as a natural categorical abstraction of the notions of subset
of a set, subgroup
of a group
, and more generally subalgebra
of any algebraic structure
, predates the notion of topos. It is definable in any category, not just toposes, in second-order
language, i.e. in terms of classes of morphisms instead of individual morphisms, as follows. Given two monics m, n from respectively Y and Z to X, we say that m ≤ n when there exists a morphism p: Y → Z for which np = m, inducing a preorder
on monics to X. When m ≤ n and n ≤ m we say that m and n are equivalent. The subobjects of X are the resulting equivalence classes of the monics to it.
In a topos "subobject" becomes, at least implicitly, a first-order notion, as follows.
As noted above, a topos is a category C having all finite limits and hence in particular the empty limit or final object 1. It is then natural to treat morphisms of the form x: 1 → X as elements x ∈ X. Morphisms f: X → Y thus correspond to functions mapping each element x ∈ X to the element fx ∈ Y, with application realized by composition.
One might then think to define a subobject of X as an equivalence class of monics m: X → X having the same image
or range
{ mx| x ∈ X }. The catch is that two or more morphisms may correspond to the same function, that is, we cannot assume that C is concrete in the sense that the functor C(1,-): C → Set is faithful. For example the category Grph of graphs and their associated homomorphism
s is a topos whose final object 1 is the graph with one vertex and one edge (a self-loop), but is not concrete because the elements 1 → G of a graph G correspond only to the self-loops and not the other edges, nor the vertices without self-loops. Whereas the second-order definition makes G and its set of self-loops (with their vertices) distinct subobjects of G (unless every edge is, and every vertex has, a self-loop), this image-based one does not. This can be addressed for the graph example and related examples via the Yoneda Lemma
as described in the Examples section below, but this then ceases to be first-order. Toposes provide a more abstract, general, and first-order solution.
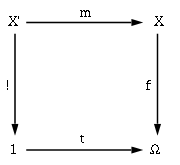 As noted above a topos C has a subobject classifier
As noted above a topos C has a subobject classifier
Ω, namely an object of C with an element t ∈ Ω, the generic subobject of C, having the property that every monic
m: X → X arises as a pullback of the generic subobject along a unique morphism f: X → Ω, as per Figure 1. Now the pullback of a monic is a monic, and all elements including t are monics since there is only one morphism to 1 from any given object, whence the pullback of t along f: X → Ω is a monic. The monics to X are therefore in bijection with the pullbacks of t along morphisms from X to Ω. The latter morphisms partition the monics into equivalence classes each determined by a morphism f: X → Ω, the characteristic morphism of that class, which we take to be the subobject of X characterized or named by f.
All this applies to any topos, whether or not concrete. In the concrete case, namely C(1,-) faithful, for example the category of sets, the situation reduces to the familiar behavior of functions. Here the monics m: X → X are exactly the injections (one-one functions) from X to X, and those with a given image { mx | x ∈ X } constitute the subobject of X corresponding to the morphism f: X → Ω for which f−1(t) is that image. The monics of a subobject will in general have many domains, all of which however will be in bijection with each other.
To summarize, this first-order notion of subobject classifier implicitly defines for a topos the same equivalence relation on monics to X as had previously been defined explicitly by the second-order notion of subobject for any category. The notion of equivalence relation on a class of morphisms is itself intrinsically second-order, which the definition of topos neatly sidesteps by explicitly defining only the notion of subobject classifier Ω, leaving the notion of subobject of X as an implicit consequence characterized (and hence namable) by its associated morphism f: X → Ω.
SetC (consisting of all covariant functor
s from C to sets, with natural transformation
s as morphisms) is a topos. For instance, the category Grph of graphs of the kind permitting multiple directed edges between two vertices is a topos. A graph consists of two sets, an edge set and a vertex set, and two functions s,t between those sets, assigning to every edge e its source s(e) and target t(e). Grph is thus equivalent to the functor category SetC, where C is the category with two objects E and V and two morphisms s,t: E → V giving respectively the source and target of each edge.
The categories of finite sets, of finite G-sets (actions of a group G on a finite set), and of finite graphs are also toposes.
The Yoneda Lemma
asserts that Cop embeds in SetC as a full subcategory. In the graph example the embedding represents Cop as the subcategory of SetC whose two objects are V' as the one-vertex no-edge graph and E' as the two-vertex one-edge graph (both as functors), and whose two nonidentity morphisms are the two graph homomorphisms from V' to E' (both as natural transformations). The natural transformations from V' to an arbitrary graph (functor) G constitute the vertices of G while those from E' to G constitute its edges. Although SetC, which we can identify with Grph, is not made concrete by either V' or E' alone, the functor U: Grph → Set2 sending object G to the pair of sets (Grph(V' ,G), Grph(E' ,G)) and morphism h: G → H to the pair of functions (Grph(V' ,h), Grph(E' ,h)) is faithful. That is, a morphism of graphs can be understood as a pair of functions, one mapping the vertices and the other the edges, with application still realized as composition but now with multiple sorts of generalized elements. This shows that the traditional concept of a concrete category as one whose objects have an underlying set can be generalized to cater for a wider range of toposes by allowing an object to have multiple underlying sets, that is, to be multisorted.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, a topos (plural "topoi" or "toposes") is a type of category
Category (mathematics)
In mathematics, a category is an algebraic structure that comprises "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose...
that behaves like the category of sheaves of sets on a topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
. For a discussion of the history of topos theory, see the article Background and genesis of topos theory
Background and genesis of topos theory
This page gives some very general background to the mathematical idea of topos. This is an aspect of category theory, and has a reputation for being abstruse. The level of abstraction involved cannot be reduced beyond a certain point; but on the other hand context can be given...
.
Grothendieck topoi (topoi in geometry)
Since the introduction of sheaves into mathematics in the 1940s a major theme has been to study a space by studying sheaves on a space. This idea was expounded by Alexander GrothendieckAlexander Grothendieck
Alexander Grothendieck is a mathematician and the central figure behind the creation of the modern theory of algebraic geometry. His research program vastly extended the scope of the field, incorporating major elements of commutative algebra, homological algebra, sheaf theory, and category theory...
by introducing the notion of a topos. The main utility of this notion is in the abundance of situations in mathematics where topological intuition is very effective but an honest topological space is lacking; it is sometimes possible to find a topos formalizing the intuition. The single greatest success of this programmatic idea to date has been the introduction of the étale topos of a scheme
Scheme (mathematics)
In mathematics, a scheme is an important concept connecting the fields of algebraic geometry, commutative algebra and number theory. Schemes were introduced by Alexander Grothendieck so as to broaden the notion of algebraic variety; some consider schemes to be the basic object of study of modern...
.
Equivalent formulations
Let C be a category. A theorem of GiraudJean Giraud (mathematician)
Jean Giraud was a French mathematician, a student of Alexander Grothendieck and the author of the book "Cohomologie non abélienne" ....
states that the following are equivalent:
- There is a small category D and an inclusion C
 Presh(D) that admits a finite-limit-preserving left adjoint.
Presh(D) that admits a finite-limit-preserving left adjoint. - C is the category of sheaves on a Grothendieck site.
- C satisfies Giraud's axioms, below.
A category with these properties is called a "(Grothendieck) topos". Here Presh(D) denotes the category of contravariant functors from D to the category of sets; such a contravariant functor is frequently called a presheaf.
Giraud's axioms
Giraud's axioms for a category C are:- C has a small set of generatorGenerator (category theory)In category theory in mathematics a generator of a category \mathcal C is an object G of the category, such that for any two different morphisms f, g: X \rightarrow Y in \mathcal C, there is a morphism h : G \rightarrow X, such that the compositions f \circ h \neq g \circ h.Generators are central...
s, and admits all small colimits. Furthermore, colimits commute with fiber products. - Sums in C are disjoint. In other words, the fiber product of X and Y over their sum is the initial object in C.
- All equivalence relations in C are effective.
The last axiom needs the most explanation. If X is an object of C, an equivalence relation R on X is a map R→X×X in C
such that all the maps Hom(Y,R)→Hom(Y,X)×Hom(Y,X) are equivalence relations of sets. Since C has colimits we may form the coequalizer of the two maps R→X; call this X/R. The equivalence relation is effective if the canonical map
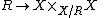
is an isomorphism.
Examples
Giraud's theorem already gives "sheaves on sites" as a complete list of examples. Note, however, that nonequivalent sites often giverise to equivalent topoi. As indicated in the introduction, sheaves on ordinary topological spaces motivate many of the basic definitions and results of topos theory.
The category of sets is an important special case: it plays the role of a point in topos theory. Indeed, a set may be thought of as a sheaf on a point.
More exotic examples, and the raison d'être of topos theory, come from algebraic geometry. To a scheme
Scheme (mathematics)
In mathematics, a scheme is an important concept connecting the fields of algebraic geometry, commutative algebra and number theory. Schemes were introduced by Alexander Grothendieck so as to broaden the notion of algebraic variety; some consider schemes to be the basic object of study of modern...
and even a stack one may associate an étale
Étale topology
In algebraic geometry, the étale topology is a Grothendieck topology on the category of schemes which has properties similar to the Euclidean topology, but unlike the Euclidean topology, it is also defined in positive characteristic...
topos, an fppf topos, a Nisnevich
Nisnevich topology
In algebraic geometry, the Nisnevich topology, sometimes called the completely decomposed topology, is a Grothendieck topology on the category of schemes which has been used in algebraic K-theory, A¹ homotopy theory, and the theory of motives...
topos...
Counterexamples
Topos theory is, in some sense, a generalization of classical point-set topology. One should therefore expect to see old and new instances of pathological
Pathological (mathematics)
In mathematics, a pathological phenomenon is one whose properties are considered atypically bad or counterintuitive; the opposite is well-behaved....
behavior. For instance, there is an example due to Pierre Deligne
Pierre Deligne
- See also :* Deligne conjecture* Deligne–Mumford moduli space of curves* Deligne–Mumford stacks* Deligne cohomology* Fourier–Deligne transform* Langlands–Deligne local constant- External links :...
of a nontrivial topos that has no points (see below).
Geometric morphisms
If X and Y are topoi, a geometric morphism u: X→Y is a pair of adjoint functors (u∗,u∗) such that u∗ preserves finite limits. Note that u∗ automatically preserves colimits by virtue of having a right adjoint.By Freyd's adjoint functor theorem, to give a geometric morphism X → Y is to give a functor u∗: Y → X that preserves finite limits and all small colimits. Thus geometric morphisms between topoi may be seen as analogues of maps of locales.
If X and Y are topological spaces and u is a continuous map between them, then the pullback and pushforward operations on sheaves yield a geometric morphism between the associated topoi.
Points of topoi
A point of a topos X is a geometric morphism from the topos of sets to X.If X is an ordinary space and x is a point of X, then the functor that takes a sheaf F to its stalk Fx has a right adjoint
(the "skyscraper sheaf" functor), so an ordinary point of X also determines a topos-theoretic point. These may be constructed as the pullback-pushforward along the continuous map x: 1 → X.
Essential geometric morphisms
A geometric morphism (u∗,u∗) is essential if u∗ has a further left adjoint u!, or equivalently (by the adjoint functor theorem) if u∗ preserves not only finite but all small limits.Ringed topoi
A ringed topos is a pair (X,R), where X is a topos and R is a commutative ring object in X. Most of the constructions of ringed spaceRinged space
In mathematics, a ringed space is, intuitively speaking, a space together with a collection of commutative rings, the elements of which are "functions" on each open set of the space...
s go through for ringed topoi. The category of R-module objects in X is an abelian category
Abelian category
In mathematics, an abelian category is a category in which morphisms and objects can be added and in which kernels and cokernels exist and have desirable properties. The motivating prototype example of an abelian category is the category of abelian groups, Ab. The theory originated in a tentative...
with enough injectives. A more useful abelian category is the subcategory of quasi-coherent R-modules: these are R-modules that admit a presentation.
Another important class of ringed topoi, besides ringed spaces, are the etale topoi of Deligne-Mumford stacks.
Homotopy theory of topoi
Michael ArtinMichael Artin
Michael Artin is an American mathematician and a professor emeritus in the Massachusetts Institute of Technology mathematics department, known for his contributions to algebraic geometry. and also generally recognized as one of the outstanding professors in his field.Artin was born in Hamburg,...
and Barry Mazur
Barry Mazur
-Life:Born in New York City, Mazur attended the Bronx High School of Science and MIT, although he did not graduate from the latter on account of failing a then-present ROTC requirement. Regardless, he was accepted for graduate school and received his Ph.D. from Princeton University in 1959,...
associated to any topos a pro-simplicial set
Pro-simplicial set
In mathematics, a pro-simplicial set is an inverse system of simplicial sets.A pro-simplicial set is called pro-finite if each term of the inverse system of simplicial sets has finite homotopy groups....
. Using this inverse system
Inverse system
In mathematics, an inverse system in a category C is a functor from a small cofiltered category I to C. An inverse system is sometimes called a pro-object in C. The dual concept is a direct system.-The category of inverse systems:...
of simplicial sets one may sometimes associate to a homotopy invariant in classical topology an inverse system
Inverse system
In mathematics, an inverse system in a category C is a functor from a small cofiltered category I to C. An inverse system is sometimes called a pro-object in C. The dual concept is a direct system.-The category of inverse systems:...
of invariants in topos theory.
The pro-simplicial set associated to the etale topos of a scheme is a pro-finite
Pro-simplicial set
In mathematics, a pro-simplicial set is an inverse system of simplicial sets.A pro-simplicial set is called pro-finite if each term of the inverse system of simplicial sets has finite homotopy groups....
simplicial set. Its study is called étale homotopy theory.
Introduction
A traditional axiomatic foundation of mathematics is set theorySet theory
Set theory is the branch of mathematics that studies sets, which are collections of objects. Although any type of object can be collected into a set, set theory is applied most often to objects that are relevant to mathematics...
, in which all mathematical objects are ultimately represented by sets (even functions
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
which map between sets). More recent work in category theory
Category theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
allows this foundation to be generalized using toposes; each topos completely defines its own mathematical framework. The category of sets forms a familiar topos, and working within this topos is equivalent to using traditional set theoretic mathematics. But one could instead choose to work with many alternative toposes. A standard formulation of the axiom of choice makes sense in any topos, and there are toposes in which it is invalid. Constructivists will be interested to work in a topos without the law of excluded middle
Law of excluded middle
In logic, the law of excluded middle is the third of the so-called three classic laws of thought. It states that for any proposition, either that proposition is true, or its negation is....
. If symmetry under a particular group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
G is of importance, one can use the topos consisting of all G-sets
Group action
In algebra and geometry, a group action is a way of describing symmetries of objects using groups. The essential elements of the object are described by a set, and the symmetries of the object are described by the symmetry group of this set, which consists of bijective transformations of the set...
.
It is also possible to encode an algebraic theory
Universal algebra
Universal algebra is the field of mathematics that studies algebraic structures themselves, not examples of algebraic structures....
, such as the theory of group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
s, as a topos. The individual models of the theory, i.e. the groups in our example, then correspond to functor
Functor
In category theory, a branch of mathematics, a functor is a special type of mapping between categories. Functors can be thought of as homomorphisms between categories, or morphisms when in the category of small categories....
s from the encoding topos to the category of sets that respect the topos structure.
Formal definition
When used for foundational work a topos will be defined axiomatically; set theory is then treated as a special case of topos theory. Building from category theory, there are multiple equivalent definitions of a topos. The following has the virtue of being concise:A topos is a category
Category theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
which has the following two properties:
- All limitsLimit (category theory)In category theory, a branch of mathematics, the abstract notion of a limit captures the essential properties of universal constructions such as products and inverse limits....
taken over finite index categories exist. - Every object has a power object. This plays the role of the powerset in set theory.
Formally, a power object of an object
 is a pair
is a pair 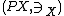 with
with 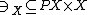 , which classifies relations, in the following sense.
, which classifies relations, in the following sense.First note that for every object
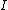 , a morphism
, a morphism 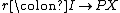 ("a family of subsets") induces a subobject
("a family of subsets") induces a subobject 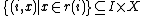 . Formally, this is defined by pulling back
. Formally, this is defined by pulling back 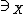 along
along 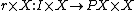 . The universal property of a power object is that every relation arises in this way, giving a bijective correspondence between relations
. The universal property of a power object is that every relation arises in this way, giving a bijective correspondence between relations 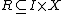 and morphisms
and morphisms 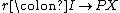 .
.From finite limits and power objects one can derive that
- All colimitsLimit (category theory)In category theory, a branch of mathematics, the abstract notion of a limit captures the essential properties of universal constructions such as products and inverse limits....
taken over finite index categories exist. - The category has a subobject classifierSubobject classifierIn category theory, a subobject classifier is a special object Ω of a category; intuitively, the subobjects of an object X correspond to the morphisms from X to Ω. As the name suggests, what a subobject classifier does is to identify/classify subobjects of a given object according to which elements...
. - Any two objects have an exponential objectExponential objectIn mathematics, specifically in category theory, an exponential object is the categorical equivalent of a function space in set theory. Categories with all finite products and exponential objects are called cartesian closed categories...
. - The category is cartesian closedCartesian closed categoryIn category theory, a category is cartesian closed if, roughly speaking, any morphism defined on a product of two objects can be naturally identified with a morphism defined on one of the factors. These categories are particularly important in mathematical logic and the theory of programming, in...
.
In some applications, the role of the subobject classifier is pivotal, whereas power objects are not. Thus some definitions reverse the roles of what is defined and what is derived.
Explanation
A topos as defined above can be understood as a cartesian closed categoryCartesian closed category
In category theory, a category is cartesian closed if, roughly speaking, any morphism defined on a product of two objects can be naturally identified with a morphism defined on one of the factors. These categories are particularly important in mathematical logic and the theory of programming, in...
for which the notion of subobject of an object has an elementary
First-order logic
First-order logic is a formal logical system used in mathematics, philosophy, linguistics, and computer science. It goes by many names, including: first-order predicate calculus, the lower predicate calculus, quantification theory, and predicate logic...
or first-order definition. This notion, as a natural categorical abstraction of the notions of subset
Subset
In mathematics, especially in set theory, a set A is a subset of a set B if A is "contained" inside B. A and B may coincide. The relationship of one set being a subset of another is called inclusion or sometimes containment...
of a set, subgroup
Subgroup
In group theory, given a group G under a binary operation *, a subset H of G is called a subgroup of G if H also forms a group under the operation *. More precisely, H is a subgroup of G if the restriction of * to H x H is a group operation on H...
of a group
Group (mathematics)
In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...
, and more generally subalgebra
Subalgebra
In mathematics, the word "algebra", when referring to a structure, often means a vector space or module equipped with an additional bilinear operation. Algebras in universal algebra are far more general: they are a common generalisation of all algebraic structures...
of any algebraic structure
Algebraic structure
In abstract algebra, an algebraic structure consists of one or more sets, called underlying sets or carriers or sorts, closed under one or more operations, satisfying some axioms. Abstract algebra is primarily the study of algebraic structures and their properties...
, predates the notion of topos. It is definable in any category, not just toposes, in second-order
Second-order logic
In logic and mathematics second-order logic is an extension of first-order logic, which itself is an extension of propositional logic. Second-order logic is in turn extended by higher-order logic and type theory....
language, i.e. in terms of classes of morphisms instead of individual morphisms, as follows. Given two monics m, n from respectively Y and Z to X, we say that m ≤ n when there exists a morphism p: Y → Z for which np = m, inducing a preorder
Preorder
In mathematics, especially in order theory, preorders are binary relations that are reflexive and transitive.For example, all partial orders and equivalence relations are preorders...
on monics to X. When m ≤ n and n ≤ m we say that m and n are equivalent. The subobjects of X are the resulting equivalence classes of the monics to it.
In a topos "subobject" becomes, at least implicitly, a first-order notion, as follows.
As noted above, a topos is a category C having all finite limits and hence in particular the empty limit or final object 1. It is then natural to treat morphisms of the form x: 1 → X as elements x ∈ X. Morphisms f: X → Y thus correspond to functions mapping each element x ∈ X to the element fx ∈ Y, with application realized by composition.
One might then think to define a subobject of X as an equivalence class of monics m: X → X having the same image
Image (mathematics)
In mathematics, an image is the subset of a function's codomain which is the output of the function on a subset of its domain. Precisely, evaluating the function at each element of a subset X of the domain produces a set called the image of X under or through the function...
or range
Range (mathematics)
In mathematics, the range of a function refers to either the codomain or the image of the function, depending upon usage. This ambiguity is illustrated by the function f that maps real numbers to real numbers with f = x^2. Some books say that range of this function is its codomain, the set of all...
{ mx| x ∈ X }. The catch is that two or more morphisms may correspond to the same function, that is, we cannot assume that C is concrete in the sense that the functor C(1,-): C → Set is faithful. For example the category Grph of graphs and their associated homomorphism
Homomorphism
In abstract algebra, a homomorphism is a structure-preserving map between two algebraic structures . The word homomorphism comes from the Greek language: ὁμός meaning "same" and μορφή meaning "shape".- Definition :The definition of homomorphism depends on the type of algebraic structure under...
s is a topos whose final object 1 is the graph with one vertex and one edge (a self-loop), but is not concrete because the elements 1 → G of a graph G correspond only to the self-loops and not the other edges, nor the vertices without self-loops. Whereas the second-order definition makes G and its set of self-loops (with their vertices) distinct subobjects of G (unless every edge is, and every vertex has, a self-loop), this image-based one does not. This can be addressed for the graph example and related examples via the Yoneda Lemma
Yoneda lemma
In mathematics, specifically in category theory, the Yoneda lemma is an abstract result on functors of the type morphisms into a fixed object. It is a vast generalisation of Cayley's theorem from group theory...
as described in the Examples section below, but this then ceases to be first-order. Toposes provide a more abstract, general, and first-order solution.

Subobject classifier
In category theory, a subobject classifier is a special object Ω of a category; intuitively, the subobjects of an object X correspond to the morphisms from X to Ω. As the name suggests, what a subobject classifier does is to identify/classify subobjects of a given object according to which elements...
Ω, namely an object of C with an element t ∈ Ω, the generic subobject of C, having the property that every monic
Monomorphism
In the context of abstract algebra or universal algebra, a monomorphism is an injective homomorphism. A monomorphism from X to Y is often denoted with the notation X \hookrightarrow Y....
m: X → X arises as a pullback of the generic subobject along a unique morphism f: X → Ω, as per Figure 1. Now the pullback of a monic is a monic, and all elements including t are monics since there is only one morphism to 1 from any given object, whence the pullback of t along f: X → Ω is a monic. The monics to X are therefore in bijection with the pullbacks of t along morphisms from X to Ω. The latter morphisms partition the monics into equivalence classes each determined by a morphism f: X → Ω, the characteristic morphism of that class, which we take to be the subobject of X characterized or named by f.
All this applies to any topos, whether or not concrete. In the concrete case, namely C(1,-) faithful, for example the category of sets, the situation reduces to the familiar behavior of functions. Here the monics m: X → X are exactly the injections (one-one functions) from X to X, and those with a given image { mx | x ∈ X } constitute the subobject of X corresponding to the morphism f: X → Ω for which f−1(t) is that image. The monics of a subobject will in general have many domains, all of which however will be in bijection with each other.
To summarize, this first-order notion of subobject classifier implicitly defines for a topos the same equivalence relation on monics to X as had previously been defined explicitly by the second-order notion of subobject for any category. The notion of equivalence relation on a class of morphisms is itself intrinsically second-order, which the definition of topos neatly sidesteps by explicitly defining only the notion of subobject classifier Ω, leaving the notion of subobject of X as an implicit consequence characterized (and hence namable) by its associated morphism f: X → Ω.
Further examples
If C is a small category, then the functor categoryFunctor category
In category theory, a branch of mathematics, the functors between two given categories form a category, where the objects are the functors and the morphisms are natural transformations between the functors...
SetC (consisting of all covariant functor
Functor
In category theory, a branch of mathematics, a functor is a special type of mapping between categories. Functors can be thought of as homomorphisms between categories, or morphisms when in the category of small categories....
s from C to sets, with natural transformation
Natural transformation
In category theory, a branch of mathematics, a natural transformation provides a way of transforming one functor into another while respecting the internal structure of the categories involved. Hence, a natural transformation can be considered to be a "morphism of functors". Indeed this intuition...
s as morphisms) is a topos. For instance, the category Grph of graphs of the kind permitting multiple directed edges between two vertices is a topos. A graph consists of two sets, an edge set and a vertex set, and two functions s,t between those sets, assigning to every edge e its source s(e) and target t(e). Grph is thus equivalent to the functor category SetC, where C is the category with two objects E and V and two morphisms s,t: E → V giving respectively the source and target of each edge.
The categories of finite sets, of finite G-sets (actions of a group G on a finite set), and of finite graphs are also toposes.
The Yoneda Lemma
Yoneda lemma
In mathematics, specifically in category theory, the Yoneda lemma is an abstract result on functors of the type morphisms into a fixed object. It is a vast generalisation of Cayley's theorem from group theory...
asserts that Cop embeds in SetC as a full subcategory. In the graph example the embedding represents Cop as the subcategory of SetC whose two objects are V' as the one-vertex no-edge graph and E' as the two-vertex one-edge graph (both as functors), and whose two nonidentity morphisms are the two graph homomorphisms from V' to E' (both as natural transformations). The natural transformations from V' to an arbitrary graph (functor) G constitute the vertices of G while those from E' to G constitute its edges. Although SetC, which we can identify with Grph, is not made concrete by either V' or E' alone, the functor U: Grph → Set2 sending object G to the pair of sets (Grph(V' ,G), Grph(E' ,G)) and morphism h: G → H to the pair of functions (Grph(V' ,h), Grph(E' ,h)) is faithful. That is, a morphism of graphs can be understood as a pair of functions, one mapping the vertices and the other the edges, with application still realized as composition but now with multiple sorts of generalized elements. This shows that the traditional concept of a concrete category as one whose objects have an underlying set can be generalized to cater for a wider range of toposes by allowing an object to have multiple underlying sets, that is, to be multisorted.
See also
- Background and genesis of topos theoryBackground and genesis of topos theoryThis page gives some very general background to the mathematical idea of topos. This is an aspect of category theory, and has a reputation for being abstruse. The level of abstraction involved cannot be reduced beyond a certain point; but on the other hand context can be given...
- Category theoryCategory theoryCategory theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
- Intuitionistic type theoryIntuitionistic type theoryIntuitionistic type theory, or constructive type theory, or Martin-Löf type theory or just Type Theory is a logical system and a set theory based on the principles of mathematical constructivism. Intuitionistic type theory was introduced by Per Martin-Löf, a Swedish mathematician and philosopher,...

