
Additive category
Encyclopedia
In mathematics
, specifically in category theory
, an additive category is a preadditive category
C such that all finite collections of objects A1,...,An of C have a biproduct
A1 ⊕ ⋯ ⊕ An in C.
(Recall that a category C is preadditive
if all its hom-sets are Abelian groups and composition of morphisms is bilinear
; in other words, C is enriched
over the monoidal category
of Abelian groups. Recall also that a biproduct
in a preadditive category is both a finite product
and a finite coproduct
.)
Warning:
The term "additive category" is sometimes applied to any preadditive category, but Wikipedia does not follow this older practice.
Note that a category is called preadditive
if just the second holds, whereas it is called semiadditive if both the first and the third hold.
Also, since the empty biproduct is a zero object in the category, we may omit the first condition. If we do this, however, we need to presuppose that the category C has zero morphisms, or equivalently that C is enriched
over the category of pointed set
s.
Ab. The zero object is the trivial group
, the addition of morphisms is given point-wise, and biproducts are given by direct sums.
More generally, every module category over a ring
R is additive, and so in particular, the category of vector spaces
over a field
K is additive.
The algebra of matrices
over a ring, thought of as a category as described below, is also additive.
Then every hom-set has an addition, endowing it with the structure of an abelian monoid, and such that the composition of morphisms is bilinear.
Moreover, if C is additive, then the two additions on hom-sets must agree. In particular, a semiadditive category is additive if and only if every morphism has an additive inverse.
This shows that the addition law for an additive category is internal to that category.
To define the addition law, we will use the convention that for a biproduct, pk will denote the projection morphisms, and ik will denote the injection morphisms.
We first observe that for each object A there is a
Next, given two morphisms αk: A → B, there exists a unique morphism α1 ⊕ α2: A ⊕ A → B ⊕ B such that pl ∘ (α1 ⊕ α2) ∘ ik equals αk if k = l, and 0 otherwise.
We can therefore define α1 + α2 := ∇ ∘ (α1 ⊕ α2) ∘ ∆.
This addition is both commutative and associative. The associativty can be seen by considering the composition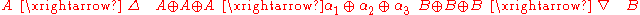
We have α + 0 = α, using that α ⊕ 0 = i1 ∘ α ∘ p1.
It is also bilinear, using for example that ∆ ∘ β = (β ⊕ β) ∘ ∆ and that (α1 ⊕ α2) ∘ (β1 ⊕ β2) = (α1 ∘ β1) ⊕ (α2 ∘ β2).
We remark that for a biproduct A ⊕ B we have i1 ∘ p1 + i2 ∘ p2 = 1. Using this, we can represent any morphism A ⊕ B → C ⊕ D as a matrix.
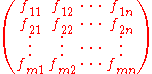 where
where 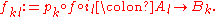
Using that ∑k ik ∘ pk = 1, it follows that addition and composition of matrices obey the usual rules for matrix addition
and matrix multiplication
.
Thus additive categories can be seen as the most general context in which the algebra of matrices makes sense.
Recall that the morphisms from a single object A to itself form the endomorphism ring
End(A).
If we denote the n-fold product of A with itself by An, then morphisms from An to Am are m-by-n matrices with entries from the ring End(A).
Conversely, given any ring
R, we can form a category Mat(R) by taking objects An indexed by the set of natural number
s (including zero
) and letting the hom-set of morphisms from An to Am be the set of m-by-n matrices over R, and where composition is given by matrix multiplication. Then Mat(R) is an additive category, and An equals the n-fold power (A1)n.
This construction should be compared with the result that a ring is a preadditive category with just one object, shown here.
If we interpret the object An as the left module
Rn, then this matrix category becomes a subcategory
of the category of left modules over R.
This may be confusing in the special case where m or n is zero, because we usually don't think of matrices with 0 rows or 0 columns. This concept makes sense, however: such matrices have no entries and so are completely determined by their size. While these matrices are rather degenerate, they do need to be included to get an additive category, since an additive category must have a zero object.
Thinking about such matrices can be useful in one way, though: they highlight the fact that given any objects A and B in an additive category, there is exactly one morphism from A to 0 (just as there is exactly one 0-by-1 matrix with entries in End(A)) and exactly one morphism from 0 to B (just as there is exactly one 1-by-0 matrix with entries in End(B)) -- this is just what it means to say that 0 is a zero object. Furthermore, the zero morphism from A to B is the composition of these morphisms, as can be calculated by multiplying the degenerate matrices.
on each hom-set in C. If the categories are additive, though, then a functor is additive if and only if it preserves all biproduct
diagrams.
That is, if B is a biproduct of A1, ..., An in C with projection morphisms pk and injection morphisms kj, then F(B) should be a biproduct of F(A1), ..., F(An) in D with projection morphisms F(pk) and injection morphisms F(ik).
Almost all functors studied between additive categories are additive. In fact, it is a theorem that all adjoint functors between additive categories must be additive functors (see here), and most interesting functors studied in all of category theory are adjoints.
The additive categories most commonly studied are in fact abelian categories; for example, Ab is an abelian category.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, specifically in category theory
Category theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
, an additive category is a preadditive category
Preadditive category
In mathematics, specifically in category theory, a preadditive category is a category that is enriched over the monoidal category of abelian groups...
C such that all finite collections of objects A1,...,An of C have a biproduct
Biproduct
In category theory and its applications to mathematics, a biproduct of a finite collection of objects in a category with zero object is both a product and a coproduct. In a preadditive category the notions of product and coproduct coincide for finite collections of objects...
A1 ⊕ ⋯ ⊕ An in C.
(Recall that a category C is preadditive
Preadditive category
In mathematics, specifically in category theory, a preadditive category is a category that is enriched over the monoidal category of abelian groups...
if all its hom-sets are Abelian groups and composition of morphisms is bilinear
Bilinear
Bilinear may refer to:* Bilinear sampling, a method in computer graphics for choosing the color of a texture* Bilinear form* Bilinear interpolation* Bilinear map, a type of mathematical function between vector spaces...
; in other words, C is enriched
Enriched category
In category theory and its applications to mathematics, enriched category is a generalization of category that abstracts the set of morphisms associated with every pair of objects to an opaque object in some fixed monoidal category of "hom-objects" and then defines composition and identity solely...
over the monoidal category
Monoidal category
In mathematics, a monoidal category is a category C equipped with a bifunctorwhich is associative, up to a natural isomorphism, and an object I which is both a left and right identity for ⊗, again up to a natural isomorphism...
of Abelian groups. Recall also that a biproduct
Biproduct
In category theory and its applications to mathematics, a biproduct of a finite collection of objects in a category with zero object is both a product and a coproduct. In a preadditive category the notions of product and coproduct coincide for finite collections of objects...
in a preadditive category is both a finite product
Product (category theory)
In category theory, the product of two objects in a category is a notion designed to capture the essence behind constructions in other areas of mathematics such as the cartesian product of sets, the direct product of groups, the direct product of rings and the product of topological spaces...
and a finite coproduct
Coproduct
In category theory, the coproduct, or categorical sum, is the category-theoretic construction which includes the disjoint union of sets and of topological spaces, the free product of groups, and the direct sum of modules and vector spaces. The coproduct of a family of objects is essentially the...
.)
Warning:
The term "additive category" is sometimes applied to any preadditive category, but Wikipedia does not follow this older practice.
Definition
A category C is additive if- it has a zero object
- every hom-set Hom(A,B) has an addition, endowing it with the structure of an abelian group, and such that composition of morphisms is bilinear
- all finite biproductBiproductIn category theory and its applications to mathematics, a biproduct of a finite collection of objects in a category with zero object is both a product and a coproduct. In a preadditive category the notions of product and coproduct coincide for finite collections of objects...
s exist.
Note that a category is called preadditive
Preadditive category
In mathematics, specifically in category theory, a preadditive category is a category that is enriched over the monoidal category of abelian groups...
if just the second holds, whereas it is called semiadditive if both the first and the third hold.
Also, since the empty biproduct is a zero object in the category, we may omit the first condition. If we do this, however, we need to presuppose that the category C has zero morphisms, or equivalently that C is enriched
Enriched category
In category theory and its applications to mathematics, enriched category is a generalization of category that abstracts the set of morphisms associated with every pair of objects to an opaque object in some fixed monoidal category of "hom-objects" and then defines composition and identity solely...
over the category of pointed set
Pointed set
In mathematics, a pointed set is a set X with a distinguished element x_0\in X, which is called the basepoint. Maps of pointed sets are those functions that map one basepoint to another, i.e. a map f : X \to Y such that f = y_0. This is usually denotedf : \to .Pointed sets may be regarded as a...
s.
Examples
The original example of an additive category is the category of abelian groupsCategory of abelian groups
In mathematics, the category Ab has the abelian groups as objects and group homomorphisms as morphisms. This is the prototype of an abelian category....
Ab. The zero object is the trivial group
Trivial group
In mathematics, a trivial group is a group consisting of a single element. All such groups are isomorphic so one often speaks of the trivial group. The single element of the trivial group is the identity element so it usually denoted as such, 0, 1 or e depending on the context...
, the addition of morphisms is given point-wise, and biproducts are given by direct sums.
More generally, every module category over a ring
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
R is additive, and so in particular, the category of vector spaces
Category of vector spaces
In mathematics, especially category theory, the category K-Vect has all vector spaces over a fixed field K as objects and K-linear transformations as morphisms...
over a field
Field (mathematics)
In abstract algebra, a field is a commutative ring whose nonzero elements form a group under multiplication. As such it is an algebraic structure with notions of addition, subtraction, multiplication, and division, satisfying certain axioms...
K is additive.
The algebra of matrices
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
over a ring, thought of as a category as described below, is also additive.
Internal Characterisation of the Addition Law
Let C be a semiadditive category, so a category having- a zero object
- all finite biproducts.
Then every hom-set has an addition, endowing it with the structure of an abelian monoid, and such that the composition of morphisms is bilinear.
Moreover, if C is additive, then the two additions on hom-sets must agree. In particular, a semiadditive category is additive if and only if every morphism has an additive inverse.
This shows that the addition law for an additive category is internal to that category.
To define the addition law, we will use the convention that for a biproduct, pk will denote the projection morphisms, and ik will denote the injection morphisms.
We first observe that for each object A there is a
- diagonal morphism ∆: A → A ⊕ A satisfying pk ∘ ∆ = 1A for k = 1,2, and a
- codiagonal morphism ∇: A ⊕ A → A satisfying ∇ ∘ ik = 1A for k = 1,2.
Next, given two morphisms αk: A → B, there exists a unique morphism α1 ⊕ α2: A ⊕ A → B ⊕ B such that pl ∘ (α1 ⊕ α2) ∘ ik equals αk if k = l, and 0 otherwise.
We can therefore define α1 + α2 := ∇ ∘ (α1 ⊕ α2) ∘ ∆.
This addition is both commutative and associative. The associativty can be seen by considering the composition
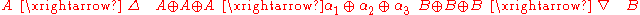
We have α + 0 = α, using that α ⊕ 0 = i1 ∘ α ∘ p1.
It is also bilinear, using for example that ∆ ∘ β = (β ⊕ β) ∘ ∆ and that (α1 ⊕ α2) ∘ (β1 ⊕ β2) = (α1 ∘ β1) ⊕ (α2 ∘ β2).
We remark that for a biproduct A ⊕ B we have i1 ∘ p1 + i2 ∘ p2 = 1. Using this, we can represent any morphism A ⊕ B → C ⊕ D as a matrix.
Matrix Representation of Morphisms
Given objects A1, ..., An and B1, ..., Bm in an additive category, we can represent morphisms f: A1 ⊕ ⋅⋅⋅ ⊕ An → B1 ⊕ ⋅⋅⋅ ⊕ Bm as m-by-n matricesMatrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
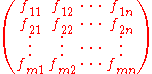 where
where 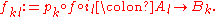
Using that ∑k ik ∘ pk = 1, it follows that addition and composition of matrices obey the usual rules for matrix addition
Matrix addition
In mathematics, matrix addition is the operation of adding two matrices by adding the corresponding entries together. However, there are other operations which could also be considered as a kind of addition for matrices, the direct sum and the Kronecker sum....
and matrix multiplication
Matrix multiplication
In mathematics, matrix multiplication is a binary operation that takes a pair of matrices, and produces another matrix. If A is an n-by-m matrix and B is an m-by-p matrix, the result AB of their multiplication is an n-by-p matrix defined only if the number of columns m of the left matrix A is the...
.
Thus additive categories can be seen as the most general context in which the algebra of matrices makes sense.
Recall that the morphisms from a single object A to itself form the endomorphism ring
Endomorphism ring
In abstract algebra, one associates to certain objects a ring, the object's endomorphism ring, which encodes several internal properties of the object; this may be denoted End...
End(A).
If we denote the n-fold product of A with itself by An, then morphisms from An to Am are m-by-n matrices with entries from the ring End(A).
Conversely, given any ring
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
R, we can form a category Mat(R) by taking objects An indexed by the set of natural number
Natural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
s (including zero
0 (number)
0 is both a numberand the numerical digit used to represent that number in numerals.It fulfills a central role in mathematics as the additive identity of the integers, real numbers, and many other algebraic structures. As a digit, 0 is used as a placeholder in place value systems...
) and letting the hom-set of morphisms from An to Am be the set of m-by-n matrices over R, and where composition is given by matrix multiplication. Then Mat(R) is an additive category, and An equals the n-fold power (A1)n.
This construction should be compared with the result that a ring is a preadditive category with just one object, shown here.
If we interpret the object An as the left module
Module (mathematics)
In abstract algebra, the concept of a module over a ring is a generalization of the notion of vector space, wherein the corresponding scalars are allowed to lie in an arbitrary ring...
Rn, then this matrix category becomes a subcategory
Subcategory
In mathematics, a subcategory of a category C is a category S whose objects are objects in C and whose morphisms are morphisms in C with the same identities and composition of morphisms. Intuitively, a subcategory of C is a category obtained from C by "removing" some of its objects and...
of the category of left modules over R.
This may be confusing in the special case where m or n is zero, because we usually don't think of matrices with 0 rows or 0 columns. This concept makes sense, however: such matrices have no entries and so are completely determined by their size. While these matrices are rather degenerate, they do need to be included to get an additive category, since an additive category must have a zero object.
Thinking about such matrices can be useful in one way, though: they highlight the fact that given any objects A and B in an additive category, there is exactly one morphism from A to 0 (just as there is exactly one 0-by-1 matrix with entries in End(A)) and exactly one morphism from 0 to B (just as there is exactly one 1-by-0 matrix with entries in End(B)) -- this is just what it means to say that 0 is a zero object. Furthermore, the zero morphism from A to B is the composition of these morphisms, as can be calculated by multiplying the degenerate matrices.
Additive functors
Recall that a functor F: C → D between preadditive categories is additive if it is an abelian group homomorphismGroup homomorphism
In mathematics, given two groups and , a group homomorphism from to is a function h : G → H such that for all u and v in G it holds that h = h \cdot h...
on each hom-set in C. If the categories are additive, though, then a functor is additive if and only if it preserves all biproduct
Biproduct
In category theory and its applications to mathematics, a biproduct of a finite collection of objects in a category with zero object is both a product and a coproduct. In a preadditive category the notions of product and coproduct coincide for finite collections of objects...
diagrams.
That is, if B is a biproduct of A1, ..., An in C with projection morphisms pk and injection morphisms kj, then F(B) should be a biproduct of F(A1), ..., F(An) in D with projection morphisms F(pk) and injection morphisms F(ik).
Almost all functors studied between additive categories are additive. In fact, it is a theorem that all adjoint functors between additive categories must be additive functors (see here), and most interesting functors studied in all of category theory are adjoints.
Special cases
- A pre-abelian categoryPre-Abelian categoryIn mathematics, specifically in category theory, a pre-abelian category is an additive category that has all kernels and cokernels.Spelled out in more detail, this means that a category C is pre-abelian if:...
is an additive category in which every morphism has a kernelKernel (category theory)In category theory and its applications to other branches of mathematics, kernels are a generalization of the kernels of group homomorphisms, the kernels of module homomorphisms and certain other kernels from algebra...
and a cokernel. - An abelian categoryAbelian categoryIn mathematics, an abelian category is a category in which morphisms and objects can be added and in which kernels and cokernels exist and have desirable properties. The motivating prototype example of an abelian category is the category of abelian groups, Ab. The theory originated in a tentative...
is a pre-abelian category such that every monomorphismMonomorphismIn the context of abstract algebra or universal algebra, a monomorphism is an injective homomorphism. A monomorphism from X to Y is often denoted with the notation X \hookrightarrow Y....
and epimorphismEpimorphismIn category theory, an epimorphism is a morphism f : X → Y which is right-cancellative in the sense that, for all morphisms ,...
is normal
The additive categories most commonly studied are in fact abelian categories; for example, Ab is an abelian category.

