Enriched category
Encyclopedia
In category theory
and its applications to mathematics
, enriched category is a generalization of category
that abstracts the set of morphisms (hom-set) associated with every pair of objects to an opaque object in some fixed monoidal category
of "hom-objects" and then defines composition and identity solely in terms of morphisms in the hom-object category. Enriched category theory thus encompasses within the same framework a wide variety of structures including
In the case where the hom-object category happens to be the monoidal category of sets and functions with the usual cartesian product, the definitions of enriched category, enriched functor, etc... reduce to the original definitions from ordinary category theory.
Enriched categories are also known as V-categories, this terminology being used in some influential texts like MacLane's; here V denotes the monoidal category of hom-objects.
, 
, 
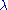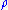) be a monoidal category
. Then an enriched category C (alternatively, in situations where the choice of monoidal category needs to be explicit, a category enriched over M, or M-category), consists of
such that the following three diagrams commute:
The first diagram expresses the associativity of composition.
Should it be the case that M is a category of sets and functions and is the usual monoidal structure (cartesian product, single-point set, etc.), each C(a,b) would then be a set whose elements are best thought of as "individual morphisms" of C while °, now a function, defines how consecutive such morphisms compose. In this case, each path leading to C(a,d) in the first diagram corresponds to one of the two ways of composing three consecutive individual morphisms from a → b → c → d from C(a,b),C(b,c) and C(c,d). Commutativity of the diagram is then merely the statement that both orders of composition give the same result, exactly as required for ordinary categories.
What is new here is that we have expressed this requirement without any explicit reference to individual morphisms in C — again, these diagrams are of morphisms in M, not C — thus making the concept of associativity of composition meaningful in the more general case where the hom-objects C(a,b) are abstract and C itself need not even have any notion of individual morphism.
Similarly, the second and third diagrams express the correponding identity rules:
If we again restrict ourselves to the case where M is a monoidal category of sets and functions, the morphisms become functions from the one-point set I and must then, for any given object a, identify a particular element of each set C(a,a), something we can then think of as the "identity morphism for a in C". Commutativity of the latter two diagrams is then the statement that compositions (as defined by the functions °) involving these distinguished individual "identity morphisms in C" behave exactly as per the identity rules for ordinary categories.
One should be careful to distinguish the different notions of "identity" being referenced here, e.g.,
from the morphisms that define the notion of identity for objects in the enriched category C, whether or not C can be considered to have individual morphisms of its own.
b ≤ c and a ≤ b ⇒ a ≤ c (transitivity)
TRUE ⇒ a ≤ a (reflexivity)
which are none other than the axioms for ≤ being a preorder. And since all diagrams in 2 commute, this is the sole content of the enriched category axioms for categories enriched over 2.
d(b,c) + d(a,b) ≥ d(a,c) (triangle inequality)
0 ≥ d(a,a)
from a monoidal category M to a monoidal category N, then any category enriched over M can be reinterpreted as a category enriched over N.
Every monoidal category M has a monoidal functor M(I, –) to the category of sets, so any enriched category has an underlying ordinary category. In many examples (such as those above) this functor is faithful, so a category enriched over M can be described as an ordinary category with certain additional structure or properties.
to enriched categories. Enriched functors are then maps between enriched categories which respect the enriched structure.
If C and D are M-categories (that is, categories enriched over monoidal category M), an M-enriched functor T: C → D is a map which assigns to each object of C an object of D and for each pair of objects a and b in C provides a morphism
in M Tab: C(a,b) → D(T(a),T(b)) between the hom-objects of C and D (which are objects in M), satisfying enriched versions of the axioms of a functor, viz preservation of identity and composition.
Because the hom-objects need not be sets in an enriched category, one cannot speak of a particular morphism. There is no longer any notion of an identity morphism, nor of a particular composition of two morphisms. Instead, morphisms from the unit to a hom-object should be thought of as selecting an identity and morphisms from the monoidal product should be thought of as composition. The usual functorial axioms are replaced with corresponding commutative diagrams involving these morphisms.
In detail, one has that the diagram
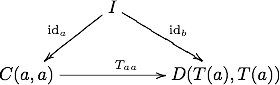
commutes, which amounts to the equation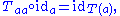
where I is the unit object of M. This is analogous to the rule F(ida) = idF(a) for ordinary functors. Additionally, one demands that the diagram
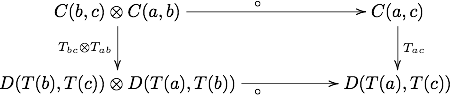
commute, which is analogous to the rule F(fg)=F(f)F(g) for ordinary functors.
Category theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
and its applications to mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, enriched category is a generalization of category
Category (mathematics)
In mathematics, a category is an algebraic structure that comprises "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose...
that abstracts the set of morphisms (hom-set) associated with every pair of objects to an opaque object in some fixed monoidal category
Monoidal category
In mathematics, a monoidal category is a category C equipped with a bifunctorwhich is associative, up to a natural isomorphism, and an object I which is both a left and right identity for ⊗, again up to a natural isomorphism...
of "hom-objects" and then defines composition and identity solely in terms of morphisms in the hom-object category. Enriched category theory thus encompasses within the same framework a wide variety of structures including
- ordinary categories in which the hom-set carries additional structure beyond being a set that needs to be preserved or otherwise accounted for (e.g., the existence of 2-cells between morphisms in a 2-category2-categoryIn category theory, a 2-category is a category with "morphisms between morphisms"; that is, where each hom set itself carries the structure of a category...
, or the addition operation on morphisms in an abelian categoryAbelian categoryIn mathematics, an abelian category is a category in which morphisms and objects can be added and in which kernels and cokernels exist and have desirable properties. The motivating prototype example of an abelian category is the category of abelian groups, Ab. The theory originated in a tentative...
) - category-like entities that don't themselves have any notion of individual morphism but whose hom-objects have similar compositional aspects (e.g., preorders where the composition rule ensures transitivity, or Lawvere's metric spaces, where the hom-objects are numerical distances and the composition rule provides the triangle inequality).
In the case where the hom-object category happens to be the monoidal category of sets and functions with the usual cartesian product, the definitions of enriched category, enriched functor, etc... reduce to the original definitions from ordinary category theory.
Enriched categories are also known as V-categories, this terminology being used in some influential texts like MacLane's; here V denotes the monoidal category of hom-objects.
Definition
Let (M,⊗,I,, , 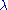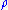) be a monoidal categoryMonoidal category
In mathematics, a monoidal category is a category C equipped with a bifunctorwhich is associative, up to a natural isomorphism, and an object I which is both a left and right identity for ⊗, again up to a natural isomorphism...
. Then an enriched category C (alternatively, in situations where the choice of monoidal category needs to be explicit, a category enriched over M, or M-category), consists of
- a classClass (set theory)In set theory and its applications throughout mathematics, a class is a collection of sets which can be unambiguously defined by a property that all its members share. The precise definition of "class" depends on foundational context...
ob(C) of objects of C, - an object C(a,b) of M for every pair of objects a,b in C,
- an arrow :I → C(a,a) designating an identity for every object a in C, and
- an arrow :C(b,c)⊗C(a,b) → C(a,c) designating a composition for each triple of objects a,b,c in C,
such that the following three diagrams commute:
The first diagram expresses the associativity of composition.
Should it be the case that M is a category of sets and functions and is the usual monoidal structure (cartesian product, single-point set, etc.), each C(a,b) would then be a set whose elements are best thought of as "individual morphisms" of C while °, now a function, defines how consecutive such morphisms compose. In this case, each path leading to C(a,d) in the first diagram corresponds to one of the two ways of composing three consecutive individual morphisms from a → b → c → d from C(a,b),C(b,c) and C(c,d). Commutativity of the diagram is then merely the statement that both orders of composition give the same result, exactly as required for ordinary categories.
What is new here is that we have expressed this requirement without any explicit reference to individual morphisms in C — again, these diagrams are of morphisms in M, not C — thus making the concept of associativity of composition meaningful in the more general case where the hom-objects C(a,b) are abstract and C itself need not even have any notion of individual morphism.
Similarly, the second and third diagrams express the correponding identity rules:
If we again restrict ourselves to the case where M is a monoidal category of sets and functions, the morphisms become functions from the one-point set I and must then, for any given object a, identify a particular element of each set C(a,a), something we can then think of as the "identity morphism for a in C". Commutativity of the latter two diagrams is then the statement that compositions (as defined by the functions °) involving these distinguished individual "identity morphisms in C" behave exactly as per the identity rules for ordinary categories.
One should be careful to distinguish the different notions of "identity" being referenced here, e.g.,
- the monoidal identity I is an object of M, being an identity for ⊗ only in the monoidMonoidIn abstract algebra, a branch of mathematics, a monoid is an algebraic structure with a single associative binary operation and an identity element. Monoids are studied in semigroup theory as they are naturally semigroups with identity. Monoids occur in several branches of mathematics; for...
-theoretic sense, and even then only up to canonical isomorphism (λ, ρ). - the identity morphisms which are actual morphisms that M has for each of its objects by virtue of it being (at least) an ordinary category.
from the morphisms that define the notion of identity for objects in the enriched category C, whether or not C can be considered to have individual morphisms of its own.
Examples of enriched categories
- Ordinary categories are categories enriched over (Set, ×, {•}), the category of sets with Cartesian productCartesian productIn mathematics, a Cartesian product is a construction to build a new set out of a number of given sets. Each member of the Cartesian product corresponds to the selection of one element each in every one of those sets...
as the monoidal operation, as noted above. - 2-Categories2-categoryIn category theory, a 2-category is a category with "morphisms between morphisms"; that is, where each hom set itself carries the structure of a category...
are categories enriched over Cat, the category of (small) categories and functors with monoidal structure being given by cartesian product. In this case the 2-cells between morphisms a → b and the vertical-composition rule that relates them correspond to the morphisms of the ordinary category C(a,b) and its own composition rule. - Locally small categories are categories enriched over (SmSet, ×), the category of small setsSmall set (category theory)In category theory, a small set is one in a fixed universe of sets . Thus, the category of small sets is the category of all sets one cares to consider...
with Cartesian product as the monoidal operation. (A locally small category is one whose hom-objects are small sets.) - Locally finite categories, by analogy, are categories enriched over (FinSet, ×), the category of finite sets with Cartesian product as the monoidal operation.
- Preordered sets are categories enriched over a certain monoidal category, 2, consisting of two objects and a single nonidentity arrow between them that we can write as FALSE → TRUE, conjunction as the monoid operation, and TRUE as its monoidal identity. The hom-objects 2(a,b) then simply deny or affirm a particular binary relation on the given pair of objects (a,b); for the sake of having more familiar notation we can write this relation as a≤b. The existence of the compositions and identity required for a category enriched over 2 immediately translate to the following axioms respectively
b ≤ c and a ≤ b ⇒ a ≤ c (transitivity)
TRUE ⇒ a ≤ a (reflexivity)
which are none other than the axioms for ≤ being a preorder. And since all diagrams in 2 commute, this is the sole content of the enriched category axioms for categories enriched over 2.
- William LawvereWilliam LawvereFrancis William Lawvere is a mathematician known for his work in category theory, topos theory and the philosophy of mathematics.-Biography:...
's generalized metric spaces, also known as pseudoquasimetric spaces, are categories enriched over the nonnegative extended real numbers , where the latter is given ordinary category structure via the inverse of its usual ordering (i.e., there exists a morphism r → s iff r ≥ s) and a monoidal structure via addition (+) and zero (0). The hom-objects are essentially distances d(a,b), and the existence of composition and identity translate to
d(b,c) + d(a,b) ≥ d(a,c) (triangle inequality)
0 ≥ d(a,a)
- Categories with zero morphisms are categories enriched over (Set*, ∧), the category of pointed sets with smash productSmash productIn mathematics, the smash product of two pointed spaces X and Y is the quotient of the product space X × Y under the identifications ∼ for all x ∈ X and y ∈ Y. The smash product is usually denoted X ∧ Y...
as the monoidal operation; the special point of a hom-object Hom(A,B) corresponds to the zero morphism from A to B. - Preadditive categoriesPreadditive categoryIn mathematics, specifically in category theory, a preadditive category is a category that is enriched over the monoidal category of abelian groups...
are categories enriched over (Ab, ⊗), the category of abelian groups with tensor product as the monoidal operation.
Relationship with monoidal functors
If there is a monoidal functorMonoidal functor
In category theory, monoidal functors are functors between monoidal categories which preserve the monoidal structure. More specifically, a monoidal functor between two monoidal categories consists of a functor between the categories, along with two coherence maps—a natural transformation and a...
from a monoidal category M to a monoidal category N, then any category enriched over M can be reinterpreted as a category enriched over N.
Every monoidal category M has a monoidal functor M(I, –) to the category of sets, so any enriched category has an underlying ordinary category. In many examples (such as those above) this functor is faithful, so a category enriched over M can be described as an ordinary category with certain additional structure or properties.
Enriched functors
An enriched functor is the appropriate generalization of the notion of a functorFunctor
In category theory, a branch of mathematics, a functor is a special type of mapping between categories. Functors can be thought of as homomorphisms between categories, or morphisms when in the category of small categories....
to enriched categories. Enriched functors are then maps between enriched categories which respect the enriched structure.
If C and D are M-categories (that is, categories enriched over monoidal category M), an M-enriched functor T: C → D is a map which assigns to each object of C an object of D and for each pair of objects a and b in C provides a morphism
Morphism
In mathematics, a morphism is an abstraction derived from structure-preserving mappings between two mathematical structures. The notion of morphism recurs in much of contemporary mathematics...
in M Tab: C(a,b) → D(T(a),T(b)) between the hom-objects of C and D (which are objects in M), satisfying enriched versions of the axioms of a functor, viz preservation of identity and composition.
Because the hom-objects need not be sets in an enriched category, one cannot speak of a particular morphism. There is no longer any notion of an identity morphism, nor of a particular composition of two morphisms. Instead, morphisms from the unit to a hom-object should be thought of as selecting an identity and morphisms from the monoidal product should be thought of as composition. The usual functorial axioms are replaced with corresponding commutative diagrams involving these morphisms.
In detail, one has that the diagram
commutes, which amounts to the equation
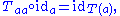
where I is the unit object of M. This is analogous to the rule F(ida) = idF(a) for ordinary functors. Additionally, one demands that the diagram
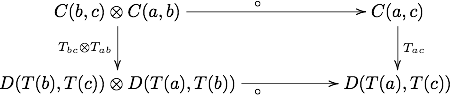
commute, which is analogous to the rule F(fg)=F(f)F(g) for ordinary functors.