Gelfond–Schneider constant
Encyclopedia
The Gelfond–Schneider constant is
which was proved to be a transcendental number
by Rodion Kuzmin
in 1930.
In 1934, Aleksandr Gelfond proved the more general Gelfond–Schneider theorem
, which solved the part of Hilbert's seventh problem
described below.
of the Gelfond–Schneider constant is the transcendental number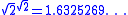
This number raised to the power of √2 is equal to 2, which illustrates that an irrational number
to the power of an irrational number can sometimes produce a rational number
.
This same constant can be used to prove that "an irrational to an irrational power may be rational", even without first proving its transcendence. The proof proceeds as follows: either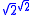
is rational, which proves the theorem, or it is irrational (as it turns out to be), and then 
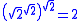is an irrational to an irrational power that is rational, which proves the theorem. The proof is not constructive
, as it does not say which of the two cases is true, but it is much simpler than Kuzmin's proof.
posed in 1900 was to prove (or find a counterexample to the claim) that ab is always transcendental for algebraic a ≠ 0, 1 and irrational algebraic b. In the address he gave two explicit examples, one of them being the Gelfond–Schneider constant 2√2.
In 1919, he gave a lecture on number theory
and spoke of three conjectures: the Riemann hypothesis
, Fermat's Last Theorem
, and the transcendence of 2√2. He mentioned to the audience that he didn't expect anyone in the hall to live long enough to see a proof of this final result. But the proof of this number's transcendence was published by Kuzmin in 1930, well within Hilbert's own lifetime. Namely, Kuzmin proved the case where the exponent b is a real quadratic irrational
, which was later extended to an arbitrary algebraic irrational b by Gelfond.
which was proved to be a transcendental number
Transcendental number
In mathematics, a transcendental number is a number that is not algebraic—that is, it is not a root of a non-constant polynomial equation with rational coefficients. The most prominent examples of transcendental numbers are π and e...
by Rodion Kuzmin
Rodion Kuzmin
Rodion Osievich Kuzmin was a Russian mathematician, known for his works in number theory and analysis.-Selected results:* 1n 1928, Kuzmin solved the following problem due to Gauss : if x is a random number chosen uniformly in , andRodion Osievich Kuzmin was a Russian mathematician, known for his...
in 1930.
In 1934, Aleksandr Gelfond proved the more general Gelfond–Schneider theorem
Gelfond–Schneider theorem
In mathematics, the Gelfond–Schneider theorem establishes the transcendence of a large class of numbers. It was originally proved independently in 1934 by Aleksandr Gelfond and Theodor Schneider...
, which solved the part of Hilbert's seventh problem
Hilbert's seventh problem
Hilbert's seventh problem is one of David Hilbert's list of open mathematical problems posed in 1900. It concerns the irrationality and transcendence of certain numbers...
described below.
Properties
The square rootSquare root
In mathematics, a square root of a number x is a number r such that r2 = x, or, in other words, a number r whose square is x...
of the Gelfond–Schneider constant is the transcendental number
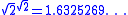
This number raised to the power of √2 is equal to 2, which illustrates that an irrational number
Irrational number
In mathematics, an irrational number is any real number that cannot be expressed as a ratio a/b, where a and b are integers, with b non-zero, and is therefore not a rational number....
to the power of an irrational number can sometimes produce a rational number
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
.
This same constant can be used to prove that "an irrational to an irrational power may be rational", even without first proving its transcendence. The proof proceeds as follows: either
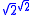is rational, which proves the theorem, or it is irrational (as it turns out to be), and then 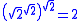is an irrational to an irrational power that is rational, which proves the theorem. The proof is not constructiveConstructive proof
In mathematics, a constructive proof is a method of proof that demonstrates the existence of a mathematical object with certain properties by creating or providing a method for creating such an object...
, as it does not say which of the two cases is true, but it is much simpler than Kuzmin's proof.
Hilbert's seventh problem
Part of the seventh of Hilbert's twenty three problemsHilbert's problems
Hilbert's problems form a list of twenty-three problems in mathematics published by German mathematician David Hilbert in 1900. The problems were all unsolved at the time, and several of them were very influential for 20th century mathematics...
posed in 1900 was to prove (or find a counterexample to the claim) that ab is always transcendental for algebraic a ≠ 0, 1 and irrational algebraic b. In the address he gave two explicit examples, one of them being the Gelfond–Schneider constant 2√2.
In 1919, he gave a lecture on number theory
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
and spoke of three conjectures: the Riemann hypothesis
Riemann hypothesis
In mathematics, the Riemann hypothesis, proposed by , is a conjecture about the location of the zeros of the Riemann zeta function which states that all non-trivial zeros have real part 1/2...
, Fermat's Last Theorem
Fermat's Last Theorem
In number theory, Fermat's Last Theorem states that no three positive integers a, b, and c can satisfy the equation an + bn = cn for any integer value of n greater than two....
, and the transcendence of 2√2. He mentioned to the audience that he didn't expect anyone in the hall to live long enough to see a proof of this final result. But the proof of this number's transcendence was published by Kuzmin in 1930, well within Hilbert's own lifetime. Namely, Kuzmin proved the case where the exponent b is a real quadratic irrational
Quadratic irrational
In mathematics, a quadratic irrational is an irrational number that is the solution to some quadratic equation with rational coefficients...
, which was later extended to an arbitrary algebraic irrational b by Gelfond.