
Four exponentials conjecture
Encyclopedia
In mathematics
, specifically the field of transcendental number theory
, the four exponentials conjecture is a conjecture
which, given the right conditions on the exponents, would guarantee the transcendence of at least one of four exponentials. The conjecture, along with two related, stronger conjectures, is at the top of a hierarchy of conjectures and theorems concerning the arithmetic nature of a certain number of values of the exponential function
.
: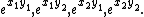
An alternative way of stating the conjecture in terms of logarithms is the following. For 1 ≤ i,j ≤ 2 let λij be complex numbers such that exp(λij) are all algebraic. Suppose λ11 and λ12 are linearly independent over the rational numbers, and λ11 and λ21 are also linearly independent over the rational numbers, then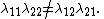
An equivalent formulation in terms of linear algebra
is the following. Let M be the 2×2 matrix
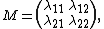
where exp(λij) is algebraic for 1 ≤ i,j ≤ 2. Suppose the two rows of M are linearly independent over the rational numbers, and the two columns of M are linearly independent over the rational numbers. Then the rank
of M is 2.
While a 2×2 matrix having linearly independent rows and columns usually means it has rank 2, in this case we require linear independence over a smaller field so the rank isn't forced to be 2. For example, the matrix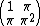
has rows and columns that are linearly independent over the rational numbers, since π is irrational. But the rank of the matrix is 1. So in this case the conjecture would imply that at least one of e, eπ, and eπ ² is transcendental (which in this case is already known since e is transcendental).
who never formally stated the conjecture. A special case of the conjecture is mentioned in a 1944 paper of Leonidas Alaoglu
and Paul Erdős
who suggest that it had been considered by Carl Ludwig Siegel
. An equivalent statement was first mentioned in print by Theodor Schneider
who set it as the first of eight important, open problems in transcendental number theory in 1957.
The related six exponentials theorem
was first explicitly mentioned in the 1960s by Serge Lang
and Kanakanahalli Ramachandra
, and both also explicitly conjecture the above result. Indeed, after proving the six exponentials theorem Lang mentions the difficulty in dropping the number of exponents from six to four — the proof used for six exponentials “just misses” when one tries to apply it to four.
and π
. For example, taking x1 = 1, x2 = √, y1 = iπ, and y2 = iπ√, the conjecture — if true — implies that one of the following four numbers is transcendental: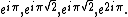
The first of these is just −1, and the fourth is 1, so the conjecture implies that eiπ√ is transcendental (which is already known, by consequence of the Gelfond–Schneider theorem
).
An open problem in number theory
settled by the conjecture is the question of whether there exists a non-integral
real number t such that both 2t and 3t are integers, or indeed such that at and bt are both integers for some pair of integers a and b that are multiplicatively independent over the integers. Values of t such that 2t is an integer are all of the form t = log2m for some integer m, while for 3t to be an integer, t must be of the form t = log3n for some integer n. At present it is unknown if there exist integers m and n, not both equal to 1, such that log2m = log3n. By setting x1 = 1, x2 = t, y1 = log2, and y2 = log3, the four exponentials conjecture implies that if t is irrational then one of the following four numbers is transcendental: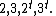
So if 2t and 3t are both integers then the conjecture implies that t must be a rational number. Since the only rational numbers t for which 2t is also rational are the integers, this implies that there are no non-integral real numbers t such that both 2t and 3t are integers. It is this consequence, for any two primes not just 2 and 3, that Alaoglu and Erdős desired in their paper as it would imply the conjecture that the quotient of two colossally abundant number
s is prime
, extending Ramanujan's
results on the quotients of consecutive superior highly composite number
.

then xi yj = βij for 1 ≤ i,j ≤ 2. So all four exponentials are in fact 1.
This conjecture implies both the sharp six exponentials theorem, which requires a third x value, and the as yet unproven sharp five exponentials conjecture that requires a further exponential to be algebraic in its hypotheses.
over the algebraic numbers generated by 1 and all logarithms of non-zero algebraic numbers, denoted here as L∗. So L∗ is the set of all complex numbers of the form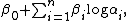
for some n ≥ 0, where all the βi and αi are algebraic and every branch of the logarithm is considered. The statement of the strong four exponentials conjecture is then as follows. Let x1, x2, and y1, y2 be two pairs of complex numbers with each pair being linearly independent over the algebraic numbers, then at least one of the four numbers xi yj for 1 ≤ i,j ≤ 2 is not in L∗.
, quadratic relations between logarithms of algebraic numbers. But a conjectural extension of Baker's theorem
implies that there should be no non-trivial algebraic relations between logarithms of algebraic numbers at all, homogeneous or not. One case of non-homogeneous quadratic relations is covered by the still open three exponentials conjecture. In its logarithmic form it is the following conjecture. Let λ1, λ2, and λ3 be any three logarithms of algebraic numbers and γ be a non-zero algebraic number, and suppose that λ1λ2 = γλ3. Then λ1λ2 = γλ3 = 0.
The exponential form of this conjecture is the following. Let x1, x2, and y be non-zero complex numbers and let γ be a non-zero algebraic number. Then at least one of the following three numbers is transcendental: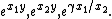
There is also a sharp three exponentials conjecture which claims that if x1, x2, and y are non-zero complex numbers and α, β1, β2, and γ are algebraic numbers such that the following three numbers are algebraic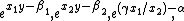
then either x2y = β2 or γx1 = α x2.
The strong three exponentials conjecture meanwhile states that if x1, x2, and y are non-zero complex numbers with x1/x2 and y/x2 both being transcendental, then at least one of the three numbers x1y, x2y, x2/x1 is not in L∗.
As with the other results in this family, the strong three exponentials conjecture implies the sharp three exponentials conjecture which implies the three exponentials conjecture. However, the strong and sharp three exponentials conjectures are implied by their four exponentials counterparts, bucking the usual trend. And the three exponentials conjecture is neither implied by nor implies the four exponentials conjecture.
The three exponentials conjecture, like the sharp five exponentials conjecture, would imply the transcendence of eπ² by letting (in the logarithmic version) λ1 = iπ, λ2 = −iπ, and γ = 1.
. Writing q = e2πi for the nome and j = J(q), Daniel Bertrand conjectured that if q1 and q2 are non-zero algebraic numbers in the complex unit disc that are multiplicatively independent, then J(q1) and J(q2) are algebraically independent over the rational numbers. Although not obviously related to the four exponentials conjecture, Bertrand's conjecture in fact implies a special case known as the weak four exponentials conjecture. This conjecture states that if x1 and x2 are two positive real algebraic numbers, neither of them equal to 1, then π² and the product are linearly independent over the rational numbers. This corresponds to the special case of the four exponentials conjecture whereby y1 = iπ, y2 = −iπ, and x1 and x2 are real. Perhaps surprisingly, though, it is also a corollary of Bertrand's conjecture, suggesting there may be an approach to the full four exponentials conjecture via the modular function j.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, specifically the field of transcendental number theory
Transcendence theory
Transcendence theory is a branch of number theory that investigates transcendental numbers, in both qualitative and quantitative ways.-Transcendence:...
, the four exponentials conjecture is a conjecture
Conjecture
A conjecture is a proposition that is unproven but is thought to be true and has not been disproven. Karl Popper pioneered the use of the term "conjecture" in scientific philosophy. Conjecture is contrasted by hypothesis , which is a testable statement based on accepted grounds...
which, given the right conditions on the exponents, would guarantee the transcendence of at least one of four exponentials. The conjecture, along with two related, stronger conjectures, is at the top of a hierarchy of conjectures and theorems concerning the arithmetic nature of a certain number of values of the exponential function
Exponential function
In mathematics, the exponential function is the function ex, where e is the number such that the function ex is its own derivative. The exponential function is used to model a relationship in which a constant change in the independent variable gives the same proportional change In mathematics,...
.
Statement
If x1, x2 and y1, y2 are two pairs of complex numbers, with each pair being linearly independent over the rational numbers, then at least one of the following four numbers is transcendentalTranscendental number
In mathematics, a transcendental number is a number that is not algebraic—that is, it is not a root of a non-constant polynomial equation with rational coefficients. The most prominent examples of transcendental numbers are π and e...
:
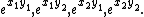
An alternative way of stating the conjecture in terms of logarithms is the following. For 1 ≤ i,j ≤ 2 let λij be complex numbers such that exp(λij) are all algebraic. Suppose λ11 and λ12 are linearly independent over the rational numbers, and λ11 and λ21 are also linearly independent over the rational numbers, then
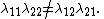
An equivalent formulation in terms of linear algebra
Linear algebra
Linear algebra is a branch of mathematics that studies vector spaces, also called linear spaces, along with linear functions that input one vector and output another. Such functions are called linear maps and can be represented by matrices if a basis is given. Thus matrix theory is often...
is the following. Let M be the 2×2 matrix
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
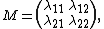
where exp(λij) is algebraic for 1 ≤ i,j ≤ 2. Suppose the two rows of M are linearly independent over the rational numbers, and the two columns of M are linearly independent over the rational numbers. Then the rank
Rank (linear algebra)
The column rank of a matrix A is the maximum number of linearly independent column vectors of A. The row rank of a matrix A is the maximum number of linearly independent row vectors of A...
of M is 2.
While a 2×2 matrix having linearly independent rows and columns usually means it has rank 2, in this case we require linear independence over a smaller field so the rank isn't forced to be 2. For example, the matrix
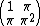
has rows and columns that are linearly independent over the rational numbers, since π is irrational. But the rank of the matrix is 1. So in this case the conjecture would imply that at least one of e, eπ, and eπ ² is transcendental (which in this case is already known since e is transcendental).
History
The conjecture was considered as early as the early 1940s by Atle SelbergAtle Selberg
Atle Selberg was a Norwegian mathematician known for his work in analytic number theory, and in the theory of automorphic forms, in particular bringing them into relation with spectral theory...
who never formally stated the conjecture. A special case of the conjecture is mentioned in a 1944 paper of Leonidas Alaoglu
Leonidas Alaoglu
Leonidas Alaoglu was a Canadian-American mathematician, most famous for his widely-cited result called Alaoglu's theorem on the weak-star compactness of the closed unit ball in the dual of a normed space, also known as the Banach–Alaoglu theorem.- Life and work :Alaoglu was born in Red Deer,...
and Paul Erdős
Paul Erdos
Paul Erdős was a Hungarian mathematician. Erdős published more papers than any other mathematician in history, working with hundreds of collaborators. He worked on problems in combinatorics, graph theory, number theory, classical analysis, approximation theory, set theory, and probability theory...
who suggest that it had been considered by Carl Ludwig Siegel
Carl Ludwig Siegel
Carl Ludwig Siegel was a mathematician specialising in number theory and celestial mechanics. He was one of the most important mathematicians of the 20th century.-Biography:...
. An equivalent statement was first mentioned in print by Theodor Schneider
Theodor Schneider
Theodor Schneider was a German mathematician, best known for providing proof of what is now known as the Gelfond–Schneider theorem in 1935....
who set it as the first of eight important, open problems in transcendental number theory in 1957.
The related six exponentials theorem
Six exponentials theorem
In mathematics, specifically transcendental number theory, the six exponentials theorem is a result that, given the right conditions on the exponents, guarantees the transcendence of at least one of a set of exponentials.-Statement:...
was first explicitly mentioned in the 1960s by Serge Lang
Serge Lang
Serge Lang was a French-born American mathematician. He was known for his work in number theory and for his mathematics textbooks, including the influential Algebra...
and Kanakanahalli Ramachandra
Kanakanahalli Ramachandra
Kanakanahalli Ramachandra was an Indian mathematician working in analytic number theory.-Early career:...
, and both also explicitly conjecture the above result. Indeed, after proving the six exponentials theorem Lang mentions the difficulty in dropping the number of exponents from six to four — the proof used for six exponentials “just misses” when one tries to apply it to four.
Corollaries
Using Euler's identity this conjecture implies the transcendence of many numbers involving eE (mathematical constant)
The mathematical constant ' is the unique real number such that the value of the derivative of the function at the point is equal to 1. The function so defined is called the exponential function, and its inverse is the natural logarithm, or logarithm to base...
and π
Pi
' is a mathematical constant that is the ratio of any circle's circumference to its diameter. is approximately equal to 3.14. Many formulae in mathematics, science, and engineering involve , which makes it one of the most important mathematical constants...
. For example, taking x1 = 1, x2 = √, y1 = iπ, and y2 = iπ√, the conjecture — if true — implies that one of the following four numbers is transcendental:
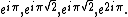
The first of these is just −1, and the fourth is 1, so the conjecture implies that eiπ√ is transcendental (which is already known, by consequence of the Gelfond–Schneider theorem
Gelfond–Schneider theorem
In mathematics, the Gelfond–Schneider theorem establishes the transcendence of a large class of numbers. It was originally proved independently in 1934 by Aleksandr Gelfond and Theodor Schneider...
).
An open problem in number theory
Number theory
Number theory is a branch of pure mathematics devoted primarily to the study of the integers. Number theorists study prime numbers as well...
settled by the conjecture is the question of whether there exists a non-integral
Integer
The integers are formed by the natural numbers together with the negatives of the non-zero natural numbers .They are known as Positive and Negative Integers respectively...
real number t such that both 2t and 3t are integers, or indeed such that at and bt are both integers for some pair of integers a and b that are multiplicatively independent over the integers. Values of t such that 2t is an integer are all of the form t = log2m for some integer m, while for 3t to be an integer, t must be of the form t = log3n for some integer n. At present it is unknown if there exist integers m and n, not both equal to 1, such that log2m = log3n. By setting x1 = 1, x2 = t, y1 = log2, and y2 = log3, the four exponentials conjecture implies that if t is irrational then one of the following four numbers is transcendental:
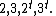
So if 2t and 3t are both integers then the conjecture implies that t must be a rational number. Since the only rational numbers t for which 2t is also rational are the integers, this implies that there are no non-integral real numbers t such that both 2t and 3t are integers. It is this consequence, for any two primes not just 2 and 3, that Alaoglu and Erdős desired in their paper as it would imply the conjecture that the quotient of two colossally abundant number
Colossally abundant number
In mathematics, a colossally abundant number is a natural number that, in some rigorous sense, has a lot of divisors...
s is prime
Prime number
A prime number is a natural number greater than 1 that has no positive divisors other than 1 and itself. A natural number greater than 1 that is not a prime number is called a composite number. For example 5 is prime, as only 1 and 5 divide it, whereas 6 is composite, since it has the divisors 2...
, extending Ramanujan's
Srinivasa Ramanujan
Srīnivāsa Aiyangār Rāmānujan FRS, better known as Srinivasa Iyengar Ramanujan was a Indian mathematician and autodidact who, with almost no formal training in pure mathematics, made extraordinary contributions to mathematical analysis, number theory, infinite series and continued fractions...
results on the quotients of consecutive superior highly composite number
Superior highly composite number
In mathematics, a superior highly composite number is a certain kind of natural number with the following properties. A natural number n is called superior highly composite if there is an ε > 0 such that for all natural numbers k ≥ 1,...
.
Sharp four exponentials conjecture
The four exponentials conjecture reduces the pair and triplet of complex numbers in the hypotheses of the six exponentials theorem to two pairs. It is conjectured that this is also possible with the sharp six exponentials theorem, and this is the sharp four exponentials conjecture. Specifically, this conjecture claims that if x1, x2, and y1, y2 are two pairs of complex numbers with each pair being linearly independent over the rational numbers, and if βij are four algebraic numbers for 1 ≤ i,j ≤ 2 such that the following four numbers are algebraic:
then xi yj = βij for 1 ≤ i,j ≤ 2. So all four exponentials are in fact 1.
This conjecture implies both the sharp six exponentials theorem, which requires a third x value, and the as yet unproven sharp five exponentials conjecture that requires a further exponential to be algebraic in its hypotheses.
Strong four exponentials conjecture
The strongest result that has been conjectured in this circle of problems is the strong four exponentials conjecture. This result would imply both aforementioned conjectures concerning four exponentials as well as all the five and six exponentials conjectures and theorems, as illustrated to the right, and all the three exponentials conjectures detailed below. The statement of this conjecture deals with the the vector spaceVector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
over the algebraic numbers generated by 1 and all logarithms of non-zero algebraic numbers, denoted here as L∗. So L∗ is the set of all complex numbers of the form
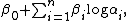
for some n ≥ 0, where all the βi and αi are algebraic and every branch of the logarithm is considered. The statement of the strong four exponentials conjecture is then as follows. Let x1, x2, and y1, y2 be two pairs of complex numbers with each pair being linearly independent over the algebraic numbers, then at least one of the four numbers xi yj for 1 ≤ i,j ≤ 2 is not in L∗.
Three exponentials conjecture
The four exponentials conjecture rules out a special case of non-trivial, homogeneousHomogeneous polynomial
In mathematics, a homogeneous polynomial is a polynomial whose monomials with nonzero coefficients all have thesame total degree. For example, x^5 + 2 x^3 y^2 + 9 x y^4 is a homogeneous polynomial...
, quadratic relations between logarithms of algebraic numbers. But a conjectural extension of Baker's theorem
Baker's theorem
In transcendence theory, a mathematical discipline, Baker's theorem gives a lower bound for linear combinations of logarithms of algebraic numbers...
implies that there should be no non-trivial algebraic relations between logarithms of algebraic numbers at all, homogeneous or not. One case of non-homogeneous quadratic relations is covered by the still open three exponentials conjecture. In its logarithmic form it is the following conjecture. Let λ1, λ2, and λ3 be any three logarithms of algebraic numbers and γ be a non-zero algebraic number, and suppose that λ1λ2 = γλ3. Then λ1λ2 = γλ3 = 0.
The exponential form of this conjecture is the following. Let x1, x2, and y be non-zero complex numbers and let γ be a non-zero algebraic number. Then at least one of the following three numbers is transcendental:
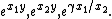
There is also a sharp three exponentials conjecture which claims that if x1, x2, and y are non-zero complex numbers and α, β1, β2, and γ are algebraic numbers such that the following three numbers are algebraic
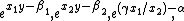
then either x2y = β2 or γx1 = α x2.
The strong three exponentials conjecture meanwhile states that if x1, x2, and y are non-zero complex numbers with x1/x2 and y/x2 both being transcendental, then at least one of the three numbers x1y, x2y, x2/x1 is not in L∗.
As with the other results in this family, the strong three exponentials conjecture implies the sharp three exponentials conjecture which implies the three exponentials conjecture. However, the strong and sharp three exponentials conjectures are implied by their four exponentials counterparts, bucking the usual trend. And the three exponentials conjecture is neither implied by nor implies the four exponentials conjecture.
The three exponentials conjecture, like the sharp five exponentials conjecture, would imply the transcendence of eπ² by letting (in the logarithmic version) λ1 = iπ, λ2 = −iπ, and γ = 1.
Bertrand's conjecture
Many of the theorems and results in transcendental number theory concerning the exponential function have analogues involving the modular function jJ-invariant
In mathematics, Klein's j-invariant, regarded as a function of a complex variable τ, is a modular function defined on the upper half-plane of complex numbers.We haveThe modular discriminant \Delta is defined as \Delta=g_2^3-27g_3^2...
. Writing q = e2πi for the nome and j = J(q), Daniel Bertrand conjectured that if q1 and q2 are non-zero algebraic numbers in the complex unit disc that are multiplicatively independent, then J(q1) and J(q2) are algebraically independent over the rational numbers. Although not obviously related to the four exponentials conjecture, Bertrand's conjecture in fact implies a special case known as the weak four exponentials conjecture. This conjecture states that if x1 and x2 are two positive real algebraic numbers, neither of them equal to 1, then π² and the product are linearly independent over the rational numbers. This corresponds to the special case of the four exponentials conjecture whereby y1 = iπ, y2 = −iπ, and x1 and x2 are real. Perhaps surprisingly, though, it is also a corollary of Bertrand's conjecture, suggesting there may be an approach to the full four exponentials conjecture via the modular function j.

