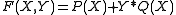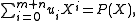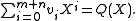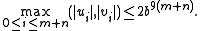Auxiliary function
Encyclopedia
In mathematics
, auxiliary functions are an important construction in transcendental number theory
. They are functions
that appear in most proofs in this area of mathematics and that have specific, desirable properties, such as taking the value zero for many arguments, or having a zero of high order
at some point.
proof that transcendental numbers exist when he showed that the so called Liouville numbers were transcendental. He did this by discovering a transcendence criterion which these numbers satisfied. To derive this criterion he started with a general algebraic number
α and found some property that this number would necessarily satisfy. The auxiliary function he used in the course of proving this criterion was simply the minimal polynomial
of α, which is the irreducible polynomial f with integer coefficients such that f(α) = 0. This function can be used to estimate how well the algebraic number α can be estimated by rational number
s p/q. Specifically if α has degree d at least two then he showed that
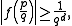
and also, using the mean value theorem
, that there is some constant depending on α, say c(α), such that
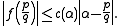
Combining these results gives a property that the algebraic number must satisfy; therefore any number not satisfying this criterion must be transcendental.
The auxiliary function in Liouville's work is very simple, merely a polynomial that vanishes at a given algebraic number. This kind of property is usually the one that auxiliary functions satisfy. They either vanish or become very small at particular points, which is usually combined with the assumption that they do not vanish or can't be too small to derive a result.
proof of the irrationality of e, though the notation used usually disguises this fact. Fourier's proof used the power series of the exponential function
: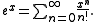
By truncating this power series after, say, N + 1 terms we get a polynomial with rational coefficients of degree N which is in some sense "close" to the function ex. Specifically if we look at the auxiliary function defined by the remainder: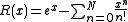
then this function—an exponential polynomial
—should take small values for x close to zero. If e is a rational number then by letting x = 1 in the above formula we see that R(1) is also a rational number. However, Fourier proved that R(1) could not be rational by eliminating every possible denominator. Thus e cannot be rational.
, that is a quotient of two polynomials. In particular he chose polynomials A(x) and B(x) such that the auxiliary function R defined by
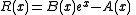
could be made as small as he wanted around x = 0. But if er were rational then R(r) would have to be rational with a particular denominator, yet Hermite could make R(r) too small to have such a denominator, hence a contradiction.
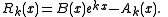
For his contradiction Hermite supposed that e satisfied the polynomial equation with integer coefficients a0 + a1e + ... + amem = 0. Multiplying this expression through by B(1) he noticed that it implied
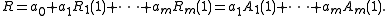
The right hand side is an integer and so, by estimating the auxiliary functions and proving that 0 < |R| < 1 he derived the necessary contradiction.
and Carl Ludwig Siegel
in the twentieth century was the realisation that these functions don't necessarily need to be explicitly known – it can be enough to know they exist and have certain properties. Using the Pigeonhole Principle Thue, and later Siegel, managed to prove the existence of auxiliary functions which, for example, took the value zero at many different points, or took high order zeros at a smaller collection of points. Moreover they proved it was possible to construct such functions without making the functions too large. Their auxiliary functions were not explicit functions, then, but by knowing that a certain function with certain properties existed, they used its properties to simplify the transcendence proofs of the nineteenth century and give several new results.
This method was picked up on and used by several other mathematicians, including Alexander Gelfond
and Theodor Schneider
who used it independently to prove the Gelfond–Schneider theorem
. Alan Baker also used the method in the 1960s for his work on linear forms in logarithms and ultimately Baker's theorem
. Another example of the use of this method from the 1960s is outlined below.
Then there exists
such that
The auxiliary polynomial theorem states
proved a result using this non-explicit form of auxiliary functions. The theorem implies both the Hermite–Lindemann and Gelfond–Schneider theorem
s. The theorem deals with a number field K and meromorphic functions f1,...,fN of order
at most ρ, at least two of which are algebraically independent, and such that if we differentiate any of these functions then the result is a polynomial in all of the functions. Under these hypotheses the theorem states that if there are m distinct complex number
s ω1,...,ωm such that fi (ωj ) is in K for all combinations of i and j, then m is bounded by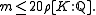
To prove the result Lang took two algebraically independent functions from f1,...,fN, say f and g, and then created an auxiliary function which was simply a polynomial F in f and g. This auxiliary function could not be explicitly stated since f and g are not explicitly known. But using Siegel's lemma
Lang showed how to make F in such a way that it vanished to a high order at the m complex numbers
ω1,...,ωm. Because of this high order vanishing it can be shown that a high-order derivative of F takes a value of small size one of the ωis, "size" here referring to an algebraic property of a number. Using the maximum modulus principle
Lang also found a separate way to estimate the absolute values of derivatives of F, and using standard results comparing the size of a number and its absolute value he showed that these estimates were contradicted unless the claimed bound on m holds.
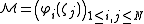
where φi are a set of functions interpolated at a set of points ζj. Since a determinant is just a polynomial in the entries of a matrix, these auxiliary functions succumb to study by analytic means. A problem with the method was the need to choose a basis before the matrix could be worked with. A development by Jean-Benoît Bost removed this problem with the use of Arakelov theory
, and research in this area is ongoing. The example below gives an idea of the flavour of this approach.
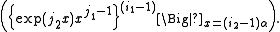
The rows of this matrix are indexed by 1 ≤ i1 ≤ n4/k and 1 ≤ i2 ≤ k, while the columns are indexed by 1 ≤ j1 ≤ n3 and 1 ≤ j2 ≤ n. So the functions in our matrix are monomials in x and ex and their derivatives, and we are interpolating at the k points 0,α,2α,...,(k − 1)α. Assuming that eα is algebraic we can form the number field Q(α,eα) of degree m over Q, and then multiply Δ by a suitable denominator as well as all its images under the embeddings of the field Q(α,eα) into C. For algebraic reasons this product is necessarily an integer, and using arguments relating to Wronskian
s it can be shown that it is non-zero, so its absolute value is an integer Ω ≥ 1.
Using a version of the mean value theorem
for matrices it is possible to get an analytic bound on Ω as well, and in fact using big-O
notation we have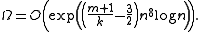
The number m is fixed by the degree of the field Q(α,eα), but k is the number of points we are interpolating at, and so we can increase it at will. And once k > 2(m + 1)/3 we will have Ω → 0, eventually contradicting the established condition Ω ≥ 1. Thus eα cannot be algebraic after all.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, auxiliary functions are an important construction in transcendental number theory
Transcendence theory
Transcendence theory is a branch of number theory that investigates transcendental numbers, in both qualitative and quantitative ways.-Transcendence:...
. They are functions
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
that appear in most proofs in this area of mathematics and that have specific, desirable properties, such as taking the value zero for many arguments, or having a zero of high order
Multiplicity (mathematics)
In mathematics, the multiplicity of a member of a multiset is the number of times it appears in the multiset. For example, the number of times a given polynomial equation has a root at a given point....
at some point.
Definition
Auxiliary functions are not a rigorously defined kind of function, rather they are functions which are either explicitly constructed or at least shown to exist and which provide a contradiction to some assumed hypothesis, or otherwise prove the result in question. Creating a function during the course of a proof in order to prove the result is not a technique exclusive to transcendence theory, but the term "auxiliary function" usually refers to the functions created in this area.Liouville's transcendence criterion
Because of the naming convention mentioned above, auxiliary functions can be dated back to their source simply by looking at the earliest results in transcendence theory. One of these first results was Liouville'sJoseph Liouville
- Life and work :Liouville graduated from the École Polytechnique in 1827. After some years as an assistant at various institutions including the Ecole Centrale Paris, he was appointed as professor at the École Polytechnique in 1838...
proof that transcendental numbers exist when he showed that the so called Liouville numbers were transcendental. He did this by discovering a transcendence criterion which these numbers satisfied. To derive this criterion he started with a general algebraic number
Algebraic number
In mathematics, an algebraic number is a number that is a root of a non-zero polynomial in one variable with rational coefficients. Numbers such as π that are not algebraic are said to be transcendental; almost all real numbers are transcendental...
α and found some property that this number would necessarily satisfy. The auxiliary function he used in the course of proving this criterion was simply the minimal polynomial
Minimal polynomial (field theory)
In field theory, given a field extension E / F and an element α of E that is an algebraic element over F, the minimal polynomial of α is the monic polynomial p, with coefficients in F, of least degree such that p = 0...
of α, which is the irreducible polynomial f with integer coefficients such that f(α) = 0. This function can be used to estimate how well the algebraic number α can be estimated by rational number
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
s p/q. Specifically if α has degree d at least two then he showed that
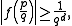
and also, using the mean value theorem
Mean value theorem
In calculus, the mean value theorem states, roughly, that given an arc of a differentiable curve, there is at least one point on that arc at which the derivative of the curve is equal to the "average" derivative of the arc. Briefly, a suitable infinitesimal element of the arc is parallel to the...
, that there is some constant depending on α, say c(α), such that
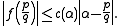
Combining these results gives a property that the algebraic number must satisfy; therefore any number not satisfying this criterion must be transcendental.
The auxiliary function in Liouville's work is very simple, merely a polynomial that vanishes at a given algebraic number. This kind of property is usually the one that auxiliary functions satisfy. They either vanish or become very small at particular points, which is usually combined with the assumption that they do not vanish or can't be too small to derive a result.
Fourier's proof of the irrationality of e
Another simple, early occurrence is in Fourier'sJoseph Fourier
Jean Baptiste Joseph Fourier was a French mathematician and physicist best known for initiating the investigation of Fourier series and their applications to problems of heat transfer and vibrations. The Fourier transform and Fourier's Law are also named in his honour...
proof of the irrationality of e, though the notation used usually disguises this fact. Fourier's proof used the power series of the exponential function
Exponential function
In mathematics, the exponential function is the function ex, where e is the number such that the function ex is its own derivative. The exponential function is used to model a relationship in which a constant change in the independent variable gives the same proportional change In mathematics,...
:
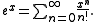
By truncating this power series after, say, N + 1 terms we get a polynomial with rational coefficients of degree N which is in some sense "close" to the function ex. Specifically if we look at the auxiliary function defined by the remainder:
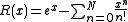
then this function—an exponential polynomial
Exponential polynomial
In mathematics, exponential polynomials are functions on fields, rings, or abelian groups that take the form of polynomials in a variable and an exponential function.-In fields:...
—should take small values for x close to zero. If e is a rational number then by letting x = 1 in the above formula we see that R(1) is also a rational number. However, Fourier proved that R(1) could not be rational by eliminating every possible denominator. Thus e cannot be rational.
Hermite's proof of the irrationality of er
Hermite extended the work of Fourier by approximating the function ex not with a polynomial but with a rational functionRational function
In mathematics, a rational function is any function which can be written as the ratio of two polynomial functions. Neither the coefficients of the polynomials nor the values taken by the function are necessarily rational.-Definitions:...
, that is a quotient of two polynomials. In particular he chose polynomials A(x) and B(x) such that the auxiliary function R defined by
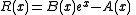
could be made as small as he wanted around x = 0. But if er were rational then R(r) would have to be rational with a particular denominator, yet Hermite could make R(r) too small to have such a denominator, hence a contradiction.
Hermite's proof of the transcendence of e
To prove that e was in fact transcendental, Hermite took his work one step further by approximating not just the function ex, but also the functions ekx for integers k = 1,...,m, where he assumed e was algebraic with degree m. By approximating ekx by rational functions with integer coefficients and with the same denominator, say Ak(x) / B(x), he could define auxiliary functions Rk(x) by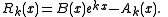
For his contradiction Hermite supposed that e satisfied the polynomial equation with integer coefficients a0 + a1e + ... + amem = 0. Multiplying this expression through by B(1) he noticed that it implied
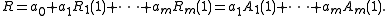
The right hand side is an integer and so, by estimating the auxiliary functions and proving that 0 < |R| < 1 he derived the necessary contradiction.
Auxiliary functions from the pigeonhole principle
The auxiliary functions sketched above can all be explicitly calculated and worked with. A breakthrough by Axel ThueAxel Thue
Axel Thue was a Norwegian mathematician, known for highly original work in diophantine approximation, and combinatorics....
and Carl Ludwig Siegel
Carl Ludwig Siegel
Carl Ludwig Siegel was a mathematician specialising in number theory and celestial mechanics. He was one of the most important mathematicians of the 20th century.-Biography:...
in the twentieth century was the realisation that these functions don't necessarily need to be explicitly known – it can be enough to know they exist and have certain properties. Using the Pigeonhole Principle Thue, and later Siegel, managed to prove the existence of auxiliary functions which, for example, took the value zero at many different points, or took high order zeros at a smaller collection of points. Moreover they proved it was possible to construct such functions without making the functions too large. Their auxiliary functions were not explicit functions, then, but by knowing that a certain function with certain properties existed, they used its properties to simplify the transcendence proofs of the nineteenth century and give several new results.
This method was picked up on and used by several other mathematicians, including Alexander Gelfond
Alexander Gelfond
Alexander Osipovich Gelfond was a Soviet mathematician, author of Gelfond's theorem.-Biography:Alexander Gelfond was born in St Petersburg, Russian Empire in the family of a professional physician and amateur philosopher Osip Isaakovich Gelfond. He entered the Moscow State University in 1924,...
and Theodor Schneider
Theodor Schneider
Theodor Schneider was a German mathematician, best known for providing proof of what is now known as the Gelfond–Schneider theorem in 1935....
who used it independently to prove the Gelfond–Schneider theorem
Gelfond–Schneider theorem
In mathematics, the Gelfond–Schneider theorem establishes the transcendence of a large class of numbers. It was originally proved independently in 1934 by Aleksandr Gelfond and Theodor Schneider...
. Alan Baker also used the method in the 1960s for his work on linear forms in logarithms and ultimately Baker's theorem
Baker's theorem
In transcendence theory, a mathematical discipline, Baker's theorem gives a lower bound for linear combinations of logarithms of algebraic numbers...
. Another example of the use of this method from the 1960s is outlined below.
Auxiliary polynomial theorem
Let β equal the cube root of b/a in the equation ax3 + bx3 = c and assume m is and integer that satisfies m + 1 > 2n/3 ≥ m ≥ 3 where n is a positive integer.Then there exists
such that
The auxiliary polynomial theorem states
A theorem of Lang
In the 1960s Serge LangSerge Lang
Serge Lang was a French-born American mathematician. He was known for his work in number theory and for his mathematics textbooks, including the influential Algebra...
proved a result using this non-explicit form of auxiliary functions. The theorem implies both the Hermite–Lindemann and Gelfond–Schneider theorem
Gelfond–Schneider theorem
In mathematics, the Gelfond–Schneider theorem establishes the transcendence of a large class of numbers. It was originally proved independently in 1934 by Aleksandr Gelfond and Theodor Schneider...
s. The theorem deals with a number field K and meromorphic functions f1,...,fN of order
Entire function
In complex analysis, an entire function, also called an integral function, is a complex-valued function that is holomorphic over the whole complex plane...
at most ρ, at least two of which are algebraically independent, and such that if we differentiate any of these functions then the result is a polynomial in all of the functions. Under these hypotheses the theorem states that if there are m distinct complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
s ω1,...,ωm such that fi (ωj ) is in K for all combinations of i and j, then m is bounded by
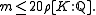
To prove the result Lang took two algebraically independent functions from f1,...,fN, say f and g, and then created an auxiliary function which was simply a polynomial F in f and g. This auxiliary function could not be explicitly stated since f and g are not explicitly known. But using Siegel's lemma
Siegel's lemma
In transcendental number theory and Diophantine approximation, Siegel's lemma refers to bounds on the solutions of linear equations obtained by the construction of auxiliary functions. The existence of these polynomials was proven by Axel Thue; Thue's proof used Dirichlet's box principle. Carl...
Lang showed how to make F in such a way that it vanished to a high order at the m complex numbers
ω1,...,ωm. Because of this high order vanishing it can be shown that a high-order derivative of F takes a value of small size one of the ωis, "size" here referring to an algebraic property of a number. Using the maximum modulus principle
Maximum modulus principle
In mathematics, the maximum modulus principle in complex analysis states that if f is a holomorphic function, then the modulus |f| cannot exhibit a true local maximum that is properly within the domain of f....
Lang also found a separate way to estimate the absolute values of derivatives of F, and using standard results comparing the size of a number and its absolute value he showed that these estimates were contradicted unless the claimed bound on m holds.
Interpolation determinants
After the myriad of successes gleaned from using existent but not explicit auxiliary functions, in the 1990s Michel Laurent introduced the idea of interpolation determinants. These are alternants – determinants of matrices of the form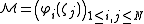
where φi are a set of functions interpolated at a set of points ζj. Since a determinant is just a polynomial in the entries of a matrix, these auxiliary functions succumb to study by analytic means. A problem with the method was the need to choose a basis before the matrix could be worked with. A development by Jean-Benoît Bost removed this problem with the use of Arakelov theory
Arakelov theory
Arakelov theory is an approach to Diophantine geometry, named for Suren Arakelov. It is used to study Diophantine equations in higher dimensions.-Background:...
, and research in this area is ongoing. The example below gives an idea of the flavour of this approach.
A proof of the Hermite–Lindemann theorem
One of the simpler applications of this method is a proof of the real version of the Hermite–Lindemann theorem. That is, if α is a non-zero, real algebraic number, then eα is transcendental. First we let k be some natural number and n be a large multiple of k. The interpolation determinant considered is the determinant Δ of the n4×n4 matrix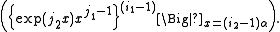
The rows of this matrix are indexed by 1 ≤ i1 ≤ n4/k and 1 ≤ i2 ≤ k, while the columns are indexed by 1 ≤ j1 ≤ n3 and 1 ≤ j2 ≤ n. So the functions in our matrix are monomials in x and ex and their derivatives, and we are interpolating at the k points 0,α,2α,...,(k − 1)α. Assuming that eα is algebraic we can form the number field Q(α,eα) of degree m over Q, and then multiply Δ by a suitable denominator as well as all its images under the embeddings of the field Q(α,eα) into C. For algebraic reasons this product is necessarily an integer, and using arguments relating to Wronskian
Wronskian
In mathematics, the Wronskian is a determinant introduced by and named by . It is used in the study of differential equations, where it can sometimes be used to show that a set of solutions is linearly independent.-Definition:...
s it can be shown that it is non-zero, so its absolute value is an integer Ω ≥ 1.
Using a version of the mean value theorem
Mean value theorem
In calculus, the mean value theorem states, roughly, that given an arc of a differentiable curve, there is at least one point on that arc at which the derivative of the curve is equal to the "average" derivative of the arc. Briefly, a suitable infinitesimal element of the arc is parallel to the...
for matrices it is possible to get an analytic bound on Ω as well, and in fact using big-O
Big O notation
In mathematics, big O notation is used to describe the limiting behavior of a function when the argument tends towards a particular value or infinity, usually in terms of simpler functions. It is a member of a larger family of notations that is called Landau notation, Bachmann-Landau notation, or...
notation we have
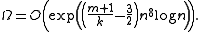
The number m is fixed by the degree of the field Q(α,eα), but k is the number of points we are interpolating at, and so we can increase it at will. And once k > 2(m + 1)/3 we will have Ω → 0, eventually contradicting the established condition Ω ≥ 1. Thus eα cannot be algebraic after all.