
Tessellation
Encyclopedia

Plane (mathematics)
In mathematics, a plane is a flat, two-dimensional surface. A plane is the two dimensional analogue of a point , a line and a space...
is a pattern of plane figures that fills the plane with no overlaps and no gaps. One may also speak of tessellations of parts of the plane or of other surfaces. Generalizations to higher dimensions are also possible. Tessellations frequently appeared in the art
Art
Art is the product or process of deliberately arranging items in a way that influences and affects one or more of the senses, emotions, and intellect....
of M. C. Escher
M. C. Escher
Maurits Cornelis Escher , usually referred to as M. C. Escher , was a Dutch graphic artist. He is known for his often mathematically inspired woodcuts, lithographs, and mezzotints...
, who was inspired by studying the Moorish use of symmetry in the Alhambra
Alhambra
The Alhambra , the complete form of which was Calat Alhambra , is a palace and fortress complex located in the Granada, Andalusia, Spain...
tiles during a visit in 1922. Tessellations are seen throughout art history, from ancient architecture to modern art
Modern art
Modern art includes artistic works produced during the period extending roughly from the 1860s to the 1970s, and denotes the style and philosophy of the art produced during that era. The term is usually associated with art in which the traditions of the past have been thrown aside in a spirit of...
.
In Latin, tessella is a small cubical piece of clay
Clay
Clay is a general term including many combinations of one or more clay minerals with traces of metal oxides and organic matter. Geologic clay deposits are mostly composed of phyllosilicate minerals containing variable amounts of water trapped in the mineral structure.- Formation :Clay minerals...
, stone
Rock (geology)
In geology, rock or stone is a naturally occurring solid aggregate of minerals and/or mineraloids.The Earth's outer solid layer, the lithosphere, is made of rock. In general rocks are of three types, namely, igneous, sedimentary, and metamorphic...
or glass
Glass
Glass is an amorphous solid material. Glasses are typically brittle and optically transparent.The most familiar type of glass, used for centuries in windows and drinking vessels, is soda-lime glass, composed of about 75% silica plus Na2O, CaO, and several minor additives...
used to make mosaic
Mosaic
Mosaic is the art of creating images with an assemblage of small pieces of colored glass, stone, or other materials. It may be a technique of decorative art, an aspect of interior decoration, or of cultural and spiritual significance as in a cathedral...
s. The word "tessella" means "small square" (from "tessera
Tessera
A tessera is an individual tile in a mosaic, usually formed in the shape of a cube. It is also known as an abaciscus, abaculus, or, in Persian کاشي معرق. In antiquity, mosaics were formed from naturally colored pebbles, but by 200 BC purpose-made tesserae were being used...
", square, which in its turn is from the Greek word for "four"). It corresponds with the everyday term tiling which refers to applications of tessellations, often made of glazed
Ceramic glaze
Glaze is a layer or coating of a vitreous substance which has been fired to fuse to a ceramic object to color, decorate, strengthen or waterproof it.-Use:...
clay.
History
In 1619 Johannes KeplerJohannes Kepler
Johannes Kepler was a German mathematician, astronomer and astrologer. A key figure in the 17th century scientific revolution, he is best known for his eponymous laws of planetary motion, codified by later astronomers, based on his works Astronomia nova, Harmonices Mundi, and Epitome of Copernican...
did one of the first documented studies of tessellations when he wrote about the regular and semiregular tessellation, which are coverings of a plane with regular polygons. Some two hundred years later in 1891, the Russian crystallographer Yevgraf Fyodorov
Yevgraf Fyodorov
Yevgraf Stepanovich Fyodorov, sometimes spelled Evgraf Stepanovich Fedorov , was a Russian mathematician, crystallographer, and mineralogist....
proved that every periodic tiling of the plane features one of seventeen different groups of isometries. Fedorov's work marked the unofficial beginning of the mathematical study of tessellations. Other prominent contributors include Shubnikov and Belov (1951); and Heinrich Heesch
Heinrich Heesch
Heinrich Heesch was a German mathematician. He was born in Kiel and died in Hanover.In Göttingen he worked on Group theory. In 1933 Heesch witnessed the National Socialist purges among the university staff...
and Otto Kienzle (1963).
Wallpaper groups
Tilings with translational symmetryTranslational symmetry
In geometry, a translation "slides" an object by a a: Ta = p + a.In physics and mathematics, continuous translational symmetry is the invariance of a system of equations under any translation...
can be categorized by wallpaper group
Wallpaper group
A wallpaper group is a mathematical classification of a two-dimensional repetitive pattern, based on the symmetries in the pattern. Such patterns occur frequently in architecture and decorative art...
s, of which 17 exist. All seventeen of these groups are represented in the Alhambra
Alhambra
The Alhambra , the complete form of which was Calat Alhambra , is a palace and fortress complex located in the Granada, Andalusia, Spain...
palace in Granada
Granada
Granada is a city and the capital of the province of Granada, in the autonomous community of Andalusia, Spain. Granada is located at the foot of the Sierra Nevada mountains, at the confluence of three rivers, the Beiro, the Darro and the Genil. It sits at an elevation of 738 metres above sea...
, Spain
Spain
Spain , officially the Kingdom of Spain languages]] under the European Charter for Regional or Minority Languages. In each of these, Spain's official name is as follows:;;;;;;), is a country and member state of the European Union located in southwestern Europe on the Iberian Peninsula...
. Of the three regular tilings two are in the p6m wallpaper group and one is in p4m.
Tessellations and color

Symmetry
Symmetry generally conveys two primary meanings. The first is an imprecise sense of harmonious or aesthetically pleasing proportionality and balance; such that it reflects beauty or perfection...
.
The four color theorem
Four color theorem
In mathematics, the four color theorem, or the four color map theorem states that, given any separation of a plane into contiguous regions, producing a figure called a map, no more than four colors are required to color the regions of the map so that no two adjacent regions have the same color...
states that for every tessellation of a normal Euclidean plane, with a set of four available colors, each tile can be colored in one color such that no tiles of equal color meet at a curve of positive length. Note that the coloring guaranteed by the four-color theorem will not in general respect the symmetries of the tessellation. To produce a coloring which does, as many as seven colors may be needed, as in the picture at right.
Tessellations with quadrilaterals
Copies of an arbitrary quadrilateralQuadrilateral
In Euclidean plane geometry, a quadrilateral is a polygon with four sides and four vertices or corners. Sometimes, the term quadrangle is used, by analogy with triangle, and sometimes tetragon for consistency with pentagon , hexagon and so on...
can form a tessellation with 2-fold rotational centers at the midpoints of all sides, and translational symmetry whose basis vectors are the diagonal of the quadrilateral or, equivalently, one of these and the sum or difference of the two. For an asymmetric quadrilateral this tiling belongs to wallpaper group p2. As fundamental domain we have the quadrilateral. Equivalently, we can construct a parallelogram subtended by a minimal set of translation vectors, starting from a rotational center. We can divide this by one diagonal, and take one half (a triangle) as fundamental domain. Such a triangle has the same area as the quadrilateral and can be constructed from it by cutting and pasting.
Regular and semi-regular tessellations

Tiling by regular polygons
Plane tilings by regular polygons have been widely used since antiquity. The first systematic mathematical treatment was that of Kepler in Harmonices Mundi.- Regular tilings :...
is a highly symmetric tessellation made up of congruent
Congruence (geometry)
In geometry, two figures are congruent if they have the same shape and size. This means that either object can be repositioned so as to coincide precisely with the other object...
regular polygon
Regular polygon
A regular polygon is a polygon that is equiangular and equilateral . Regular polygons may be convex or star.-General properties:...
s. Only three regular tessellations exist: those made up of equilateral triangles, square
Square (geometry)
In geometry, a square is a regular quadrilateral. This means that it has four equal sides and four equal angles...
s, or hexagons.
A semiregular tessellation uses a variety of regular polygons; there are eight of these. The arrangement of polygons at every vertex point is identical. An edge-to-edge tessellation is even less regular: the only requirement is that adjacent tiles only share full sides, i.e. no tile shares a partial side with any other tile. Other types of tessellations exist, depending on types of figures and types of pattern. There are regular versus irregular, periodic versus nonperiodic, symmetric versus asymmetric, and fractal
Fractal
A fractal has been defined as "a rough or fragmented geometric shape that can be split into parts, each of which is a reduced-size copy of the whole," a property called self-similarity...
tessellations, as well as other classifications.
Penrose tiling
Penrose tiling
A Penrose tiling is a non-periodic tiling generated by an aperiodic set of prototiles named after Sir Roger Penrose, who investigated these sets in the 1970s. The aperiodicity of the Penrose prototiles implies that a shifted copy of a Penrose tiling will never match the original...
s using two different polygons are the most famous example of tessellations that create aperiodic
Aperiodic tiling
An aperiodic tiling is a tiling obtained from an aperiodic set of tiles. Properly speaking, aperiodicity is a property of particular sets of tiles; any given finite tiling is either periodic or non-periodic...
patterns. They belong to a general class of aperiodic tilings that can be constructed out of self-replicating
Self-replication
Self-replication is any behavior of a dynamical system that yields construction of an identical copy of that dynamical system. Biological cells, given suitable environments, reproduce by cell division. During cell division, DNA is replicated and can be transmitted to offspring during reproduction...
sets of polygons by using recursion
Recursion
Recursion is the process of repeating items in a self-similar way. For instance, when the surfaces of two mirrors are exactly parallel with each other the nested images that occur are a form of infinite recursion. The term has a variety of meanings specific to a variety of disciplines ranging from...
.
A monohedral tiling is a tessellation in which all tiles are congruent
Congruence (geometry)
In geometry, two figures are congruent if they have the same shape and size. This means that either object can be repositioned so as to coincide precisely with the other object...
. Spiral monohedral tilings include the Voderberg tiling discovered by Hans Voderberg in 1936, whose unit tile is a nonconvex enneagon
Enneagon
In geometry, a nonagon is a nine-sided polygon.The name "nonagon" is a prefix hybrid formation, from Latin , used equivalently, attested already in the 16th century in French nonogone and in English from the 17th century...
; and the Hirschhorn tiling discovered by Michael Hirschhorn in the 1970s, whose unit tile is an irregular pentagon
Pentagon
In geometry, a pentagon is any five-sided polygon. A pentagon may be simple or self-intersecting. The sum of the internal angles in a simple pentagon is 540°. A pentagram is an example of a self-intersecting pentagon.- Regular pentagons :In a regular pentagon, all sides are equal in length and...
.
Self-dual tessellations
TilingsUniform tiling
In geometry, a uniform tiling is a tessellation of the plane by regular polygon faces with the restriction of being vertex-uniform.Uniform tilings can exist in both the Euclidean plane and hyperbolic plane...
and honeycombs
Honeycomb (geometry)
In geometry, a honeycomb is a space filling or close packing of polyhedral or higher-dimensional cells, so that there are no gaps. It is an example of the more general mathematical tiling or tessellation in any number of dimensions....
can also be self-dual. All n-dimensional hypercubic honeycombs with Schlafli symbols {4,3n−2,4}, are self-dual.
 |
Tessellations and computer models



Computer graphics
Computer graphics are graphics created using computers and, more generally, the representation and manipulation of image data by a computer with help from specialized software and hardware....
, tessellation techniques are often used to manage datasets of polygons and divide them into suitable structures for rendering
Rendering (computer graphics)
Rendering is the process of generating an image from a model , by means of computer programs. A scene file contains objects in a strictly defined language or data structure; it would contain geometry, viewpoint, texture, lighting, and shading information as a description of the virtual scene...
. Normally, at least for real-time rendering, the data is tessellated into triangles, which is sometimes referred to as triangulation
Polygon triangulation
In computational geometry, polygon triangulation is the decomposition of a polygonal area P into a set of triangles, i.e., finding the set of triangles with pairwise non-intersecting interiors whose union is P....
.
Tessellation is a staple feature of DirectX 11 and OpenGL
OpenGL
OpenGL is a standard specification defining a cross-language, cross-platform API for writing applications that produce 2D and 3D computer graphics. The interface consists of over 250 different function calls which can be used to draw complex three-dimensional scenes from simple primitives. OpenGL...
.
In computer-aided design
Computer-aided design
Computer-aided design , also known as computer-aided design and drafting , is the use of computer technology for the process of design and design-documentation. Computer Aided Drafting describes the process of drafting with a computer...
the constructed design is represented by a boundary representation topological model, where analytical 3D surfaces and curves, limited to faces and edges constitute a continuous boundary of a 3D body.
Arbitrary 3D bodies are often too complicated to analyze directly. So they are approximated (tessellated) with a mesh
Polygon mesh
A polygon mesh or unstructured grid is a collection of vertices, edges and faces that defines the shape of a polyhedral object in 3D computer graphics and solid modeling...
of small, easy-to-analyze pieces of 3D volume — usually either irregular tetrahedron
Tetrahedron
In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids...
s, or irregular hexahedron
Hexahedron
A hexahedron is any polyhedron with six faces, although usually implies the cube as a regular hexahedron with all its faces square, and three squares around each vertex....
s. The mesh is used for finite element analysis.
Mesh
Polygon mesh
A polygon mesh or unstructured grid is a collection of vertices, edges and faces that defines the shape of a polyhedral object in 3D computer graphics and solid modeling...
of a surface is usually generated per individual faces and edges (approximated to polylines) so that original limit vertices are included into mesh.
To ensure approximation of the original surface suits needs of the further processing 3 basic parameters are usually defined for the surface mesh generator:
- Maximum allowed distance between planar approximation polygon and the surface (aka "sag"). This parameter ensures that mesh is similar enough to the original analytical surface (or the polyline is similar to the original curve).
- Maximum allowed size of the approximation polygon (for triangulations it can be maximum allowed length of triangle sides). This parameter ensures enough detail for further analysis.
- Maximum allowed angle between two adjacent approximation polygons (on the same face). This parameter ensures that even very small humps or hollows that can have significant effect to analysis will not disappear in mesh.
Algorithm generating mesh is driven by the parameters.
Some computer analyses require adaptive mesh, which is made finer (using stronger parameters) in regions where the analysis needs more detail.
Some geodesic dome
Geodesic dome
A geodesic dome is a spherical or partial-spherical shell structure or lattice shell based on a network of great circles on the surface of a sphere. The geodesics intersect to form triangular elements that have local triangular rigidity and also distribute the stress across the structure. When...
s are designed by tessellating the sphere with triangles that are as close to equilateral triangles as possible.
Tessellations in nature
BasaltBasalt
Basalt is a common extrusive volcanic rock. It is usually grey to black and fine-grained due to rapid cooling of lava at the surface of a planet. It may be porphyritic containing larger crystals in a fine matrix, or vesicular, or frothy scoria. Unweathered basalt is black or grey...
ic lava flows often display column
Column
A column or pillar in architecture and structural engineering is a vertical structural element that transmits, through compression, the weight of the structure above to other structural elements below. For the purpose of wind or earthquake engineering, columns may be designed to resist lateral forces...
ar jointing as a result of contraction forces causing cracks as the lava cools. The extensive crack networks that develop often produce hexagonal columns of lava. One example of such an array of columns is the Giant's Causeway
Giant's Causeway
The Giant's Causeway is an area of about 40,000 interlocking basalt columns, the result of an ancient volcanic eruption. It is located in County Antrim on the northeast coast of Northern Ireland, about three miles northeast of the town of Bushmills...
in Northern Ireland.
The Tessellated pavement
Tessellated pavement
A tessellated pavement is a rare erosional feature formed in flat sedimentary rock formations lying on some ocean shores. The pavement bears this name because the rock has fractured into polygonal blocks that resemble tiles, or tessellations...
in Tasmania is a rare sedimentary rock formation where the rock has fractured into rectangular blocks.
Within botany, the term "tessellate" describes a checkered pattern, for example on a flower petal, tree bark, or fruit.
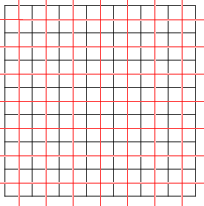
Number of sides of a polygon versus number of sides at a vertex
For an infinite tiling, let be the average number of sides of a polygon, and
be the average number of sides of a polygon, and 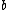 the average number of sides meeting at a vertex. Then
the average number of sides meeting at a vertex. Then  .
.For example, we have the combinations (3, 6), (3, 5), (3, 4), (4, 4), (6, 3), for the tilings in the article Tilings of regular polygons.
A continuation of a side in a straight line beyond a vertex is counted as a separate side. For example, the bricks in the picture are considered hexagons, and we have combination (6, 3). Similarly, for the basketweave tiling often found on bathroom floors, we have (5, 3).
For a tiling which repeats itself, one can take the averages over the repeating part. In the general case the averages are taken as the limits for a region expanding to the whole plane. In cases like an infinite row of tiles, or tiles getting smaller and smaller outwardly, the outside is not negligible and should also be counted as a tile while taking the limit. In extreme cases the limits may not exist, or depend on how the region is expanded to infinity.
For finite tessellations and polyhedra
Polyhedron
In elementary geometry a polyhedron is a geometric solid in three dimensions with flat faces and straight edges...
we have
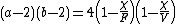
where
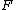 is the number of faces and
is the number of faces and 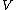 the number of vertices, and
the number of vertices, and 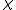 is the Euler characteristic
is the Euler characteristicEuler characteristic
In mathematics, and more specifically in algebraic topology and polyhedral combinatorics, the Euler characteristic is a topological invariant, a number that describes a topological space's shape or structure regardless of the way it is bent...
(for the plane and for a polyhedron without holes: 2), and, again, in the plane the outside counts as a face.
The formula follows observing that the number of sides of a face, summed over all faces, gives twice the total number of sides in the entire tessellation, which can be expressed in terms of the number of faces and the number of vertices. Similarly the number of sides at a vertex, summed over all vertices, also gives twice the total number of sides. From the two results the formula readily follows.
In most cases the number of sides of a face is the same as the number of vertices of a face, and the number of sides meeting at a vertex is the same as the number of faces meeting at a vertex. However, in a case like two square faces touching at a corner, the number of sides of the outer face is 8, so if the number of vertices is counted the common corner has to be counted twice. Similarly the number of sides meeting at that corner is 4, so if the number of faces at that corner is counted the face meeting the corner twice has to be counted twice.
A tile with a hole, filled with one or more other tiles, is not permissible, because the network of all sides inside and outside is disconnected. However it is allowed with a cut so that the tile with the hole touches itself. For counting the number of sides of this tile, the cut should be counted twice.
For the Platonic solid
Platonic solid
In geometry, a Platonic solid is a convex polyhedron that is regular, in the sense of a regular polygon. Specifically, the faces of a Platonic solid are congruent regular polygons, with the same number of faces meeting at each vertex; thus, all its edges are congruent, as are its vertices and...
s we get round numbers, because we take the average over equal numbers: for
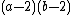 we get 1, 2, and 3.
we get 1, 2, and 3.From the formula for a finite polyhedron we see that in the case that while expanding to an infinite polyhedron the number of holes (each contributing −2 to the Euler characteristic) grows proportionally with the number of faces and the number of vertices, the limit of
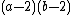 is larger than 4. For example, consider one layer of cubes, extending in two directions, with one of every 2 × 2 cubes removed. This has combination (4, 5), with
is larger than 4. For example, consider one layer of cubes, extending in two directions, with one of every 2 × 2 cubes removed. This has combination (4, 5), with  , corresponding to having 10 faces and 8 vertices per hole.
, corresponding to having 10 faces and 8 vertices per hole.Note that the result does not depend on the edges being line segments and the faces being parts of planes: mathematical rigor to deal with pathological cases aside, they can also be curves and curved surfaces.
Tessellations of other spaces
 An example tessellation of the surface of a sphere by a truncated icosidodecahedron Truncated icosidodecahedron In geometry, the truncated icosidodecahedron is an Archimedean solid, one of thirteen convex isogonal nonprismatic solids constructed by two or more types of regular polygon faces.... . |
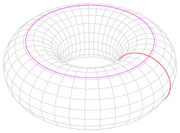 A torus Torus In geometry, a torus is a surface of revolution generated by revolving a circle in three dimensional space about an axis coplanar with the circle... can be tiled by a repeating matrix of isogonal quadrilaterals. |
 M.C.Escher, Circle Limit III (1959) |
As well as tessellating the 2-dimensional Euclidean plane, it is also possible to tessellate other n-dimensional spaces by filling them with n-dimensional polytope
Polytope
In elementary geometry, a polytope is a geometric object with flat sides, which exists in any general number of dimensions. A polygon is a polytope in two dimensions, a polyhedron in three dimensions, and so on in higher dimensions...
s. Tessellations of other spaces are often referred to as honeycombs
Honeycomb (geometry)
In geometry, a honeycomb is a space filling or close packing of polyhedral or higher-dimensional cells, so that there are no gaps. It is an example of the more general mathematical tiling or tessellation in any number of dimensions....
. Examples of tessellations of other spaces include:
- Tessellations of n-dimensional Euclidean space. For example, 3-dimensional Euclidean space can be filled with cubes to create the cubic honeycombCubic honeycombThe cubic honeycomb is the only regular space-filling tessellation in Euclidean 3-space, made up of cubic cells. It has 4 cubes around every edge, and 8 cubes around each vertex. Its vertex figure is a regular octahedron....
.
- Tessellations of n-dimensional elliptic spaceElliptic geometryElliptic geometry is a non-Euclidean geometry, in which, given a line L and a point p outside L, there exists no line parallel to L passing through p. Elliptic geometry, like hyperbolic geometry, violates Euclid's parallel postulate, which can be interpreted as asserting that there is exactly one...
, either the n-sphere (spherical tiling, spherical polyhedronSpherical polyhedronIn mathematics, a spherical polyhedron is a tiling of the sphere in which the surface is divided or partitioned by great arcs into bounded regions called spherical polygons...
) or n-dimensional real projective spaceReal projective spaceIn mathematics, real projective space, or RPn, is the topological space of lines through 0 in Rn+1. It is a compact, smooth manifold of dimension n, and a special case of a Grassmannian.-Construction:...
(elliptic tiling, projective polyhedronProjective polyhedronIn geometry, a projective polyhedron is a tessellation of the real projective plane. These are projective analogs of spherical polyhedra – tessellations of the sphere – and toroidal polyhedra – tessellations of the toroids....
).- For example, projecting the edges of a regular dodecahedron onto its circumsphere creates a tessellation of the 2-dimensional sphere with regular spherical pentagons, while taking the quotient by the antipodal map yields the hemi-dodecahedronHemi-dodecahedronA hemi-dodecahedron is an abstract regular polyhedron, containing half the faces of a regular dodecahedron. It can be realized as a projective polyhedron , which can be visualized by constructing the projective plane as a hemisphere where opposite points along the boundary are connected and...
, a tiling of the projective plane.
- For example, projecting the edges of a regular dodecahedron onto its circumsphere creates a tessellation of the 2-dimensional sphere with regular spherical pentagons, while taking the quotient by the antipodal map yields the hemi-dodecahedron
- Tessellations of n-dimensional hyperbolic spaceHyperbolic spaceIn mathematics, hyperbolic space is a type of non-Euclidean geometry. Whereas spherical geometry has a constant positive curvature, hyperbolic geometry has a negative curvature: every point in hyperbolic space is a saddle point...
. For example, M. C. EscherM. C. EscherMaurits Cornelis Escher , usually referred to as M. C. Escher , was a Dutch graphic artist. He is known for his often mathematically inspired woodcuts, lithographs, and mezzotints...
's Circle Limit III depicts a tessellation of the hyperbolic plane (using the Poincaré disk modelPoincaré disk modelIn geometry, the Poincaré disk model, also called the conformal disk model, is a model of n-dimensional hyperbolic geometry in which the points of the geometry are in an n-dimensional disk, or unit ball, and the straight lines of the hyperbolic geometry are segments of circles contained in the disk...
) with congruent fish-like shapes. The hyperbolic plane admits a tessellation with regular p-gons meeting in qs whenever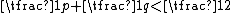 ; Circle Limit III may be understood as a tiling of octagons meeting in threes, with all sides replaced with jagged lines and each octagon then cut into four fish.
; Circle Limit III may be understood as a tiling of octagons meeting in threes, with all sides replaced with jagged lines and each octagon then cut into four fish.
See for further non-Euclidean examples.
There are also abstract polyhedra which do not correspond to a tessellation of a manifold because they are not locally spherical (locally Euclidean, like a manifold), such as the 11-cell
11-cell
In mathematics, the 11-cell is a self-dual abstract regular 4-polytope . Its 11 cells are hemi-icosahedral. It has 11 vertices, 55 edges and 55 faces. Its symmetry group is the projective special linear group L2, so it has660 symmetries...
and the 57-cell. These can be seen as tilings of more general spaces.
See also
- Coxeter groups – algebraic groups that can be used to find tessellations
- Girih tilesGirih tilesGirih tiles are a set of five tiles that were used in the creation of tiling patterns for decoration of buildings in Islamic architecture...
- Jigsaw puzzleJigsaw puzzleA jigsaw puzzle is a tiling puzzle that requires the assembly of numerous small, often oddly shaped, interlocking and tessellating pieces.Each piece usually has a small part of a picture on it; when complete, a jigsaw puzzle produces a complete picture...
- List of regular polytopes
- List of uniform tilings
- Mathematics and fiber artsMathematics and fiber artsMathematical ideas have been used as inspiration for a number of fiber arts including quilt making, knitting, cross-stitch, crochet, embroidery and weaving...
- Nikolas SchillerNikolas SchillerNikolas Schiller is an American blogger, a prominent digital map artist in the blogosphere, a vegetarian, and a civil rights activist who lives in Washington, DC...
– artist using tessellations of aerial photographs - Pinwheel tilingPinwheel tilingPinwheel tilings are non-periodic tilings defined by Charles Radin and based on a construction due to John Conway.They are the first known non-periodic tilings to each have the property that their tiles appear in infinitely many orientations....
- PolyiamondPolyiamondA polyiamond is a polyform whose base form is an equilateral triangle. The word polyiamond is a back-formation from diamond, because this word is often used to describe the shape of a pair of equilateral triangles placed base to base, and the initial "di-" looked like a Greek prefix meaning...
and PolyominoPolyominoA polyomino is a plane geometric figure formed by joining one or more equal squares edge to edge. It is a polyform whose cells are squares. It may be regarded as a finite subset of the regular square tiling with a connected interior....
— figures consisting of regular triangles and squares respectively, often appearing in tiling puzzles - QuiltingQuiltingQuilting is a sewing method done to join two or more layers of material together to make a thicker padded material. A quilter is the name given to someone who works at quilting. Quilting can be done by hand, by sewing machine, or by a specialist longarm quilting system.The process of quilting uses...
- TileTileA tile is a manufactured piece of hard-wearing material such as ceramic, stone, metal, or even glass. Tiles are generally used for covering roofs, floors, walls, showers, or other objects such as tabletops...
- Tiling puzzleTiling puzzleTiling puzzles are puzzles involving two-dimensional packing problems in which a number of flat shapes have to be assembled into a larger given shape without overlaps . Some tiling puzzles ask you to dissect a given shape first and then rearrange the pieces into another shape...
- Tilings of regular polygons
- TrianglepointTrianglepointTrianglepoint is a form of embroidery in which a series of equilateral triangles are stitched in different colors to create geometric designs, three-dimensional designs or pictures...
– needlepoint with polyiamonds (equilateral triangles) - Triangulation (geometry)
- Uniform tessellationUniform tessellationIn geometry, a uniform tessellation is a vertex-transitive tessellations made from uniform polytope facets. All of its vertices are identical and there is the same combination and arrangement of faces at each vertex....
- Uniform tilingUniform tilingIn geometry, a uniform tiling is a tessellation of the plane by regular polygon faces with the restriction of being vertex-uniform.Uniform tilings can exist in both the Euclidean plane and hyperbolic plane...
- Uniform tilings in hyperbolic planeUniform tilings in hyperbolic planeThere are an infinite number of uniform tilings on the hyperbolic plane based on the where 1/p + 1/q + 1/r ...
- Voronoi tessellation
- Wallpaper groupWallpaper groupA wallpaper group is a mathematical classification of a two-dimensional repetitive pattern, based on the symmetries in the pattern. Such patterns occur frequently in architecture and decorative art...
– seventeen types of two-dimensional repetitive patterns - Wang tiles

