Uniform tiling
Encyclopedia
In geometry
, a uniform tiling is a tessellation
of the plane by regular polygon
faces with the restriction of being vertex-uniform.
Uniform tilings can exist in both the Euclidean plane and hyperbolic plane
. Uniform tilings are related to the finite uniform polyhedra
which can be considered uniform tilings of the sphere.
Most uniform tilings can be made from a Wythoff construction
starting with a symmetry group
and a singular generator point inside of the fundamental domain. A planar symmetry group has a polygonal fundamental domain
and can be represented by the group name represented by the order of the mirrors in sequential vertices.
A fundamental domain triangle is (p q r), and a right triangle (p q 2), where p, q, r are whole numbers greater than 1. The triangle may exist as a spherical triangle, an Euclidean plane triangle, or a hyperbolic plane triangle, depending on the values of p, q and r.
There are a number of symbolic schemes for naming these figures, from a modified Schläfli symbol for right triangle domains: (p q 2) --> {p, q}. The Coxeter-Dynkin diagram
is a triangular graph with p, q, r labeled on the edges. If r = 2, the graph is linear since order-2 domain nodes generate no reflections. The Wythoff symbol
takes the 3 integers and separates them by a vertical bar (|). If the generator point is off the mirror opposite a domain node, it is given before the bar.
Finally tilings can be described by their vertex configuration
, the sequence of polygons around each vertex.
All uniform tilings can be constructed from various operations applied to regular tilings. These operations as named by Norman Johnson are called truncation
(cutting vertices), rectification
(cutting vertices until edges disappear), and Cantellation (cutting edges). Omnitruncation is an operation that combines truncation and cantellation. Snubbing is an operation of Alternate truncation of the omnitruncated form. (See Uniform polyhedron#Wythoff construction operators for more details.)
s for the plane define the Wythoff construction and can be represented by Coxeter-Dynkin diagram
s:
For groups with whole number orders, including:
These symmetry groups create 3 regular tilings, and 7 semiregular ones. A number of the semiregular tilings are repeated from different symmetry constructors.
A prismatic symmetry group represented by (2 2 2 2) represents by two sets of parallel mirrors, which in general can have a rectangular fundamental domain. It generates no new tilings.
A further prismatic symmetry group represented by (∞ 2 2) which has an infinite fundamental domain. It constructs two uniform tilings, the apeirogonal prism
and apeirogonal antiprism
.
The stacking of the finite faces of these two prismatic tilings constructs one non-Wythoffian uniform tiling of the plane. It is called the elongated triangular tiling
, composed of alternating layers of squares and triangles.
Right angle fundamental triangles: (p q 2)
General fundamental triangles: (p q r)
, each based on a different reflective symmetry group (p q r).
A sampling is shown here with a Poincaré disk
projection.
The Coxeter-Dynkin diagram
is given in a linear form, although it is actually a triangle, with the trailing segment r connecting to the first node.
Further Symmetry groups exist in the hyperbolic plane with quadrilateral fundamental domains starting with (2 2 2 3), etc, that can generate new forms. As well there's fundamental domains that place vertices at infinity, such as (∞ 2 3), etc.
Right angle fundamental triangles: (p q 2)
General fundamental triangles (p q r)
Symmetry group triangles with retrogrades include:
Symmetry group triangles with infinity include:
Branko Grünbaum
, in the 1987 book Tilings and patterns, in section 12.3 enumerates a list of 25 uniform tilings, including the 11 convex forms, and adds 14 more he calls hollow tilings which included the first two expansions above, star polygon faces and vertex figures.
H.S.M. Coxeter et al., in the 1954 paper 'Uniform polyhedra', in Table 8: Uniform Tessellations, uses all of these and enumerates a total of 38 uniform tilings.
Finally, if a tiling made of 2 apeirogons is also counted, the total can be considered 39 uniform tilings.
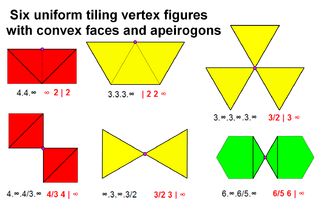The 7 new tilings with {∞} tiles, given by vertex figure
and Wythoff symbol
are:
The remaining list includes 21 tilings, 7 with {∞} tiles (apeirogons). Drawn as edge-graphs there are only 14 unique tilings, and the first is identical to the 3.4.6.4 tiling.
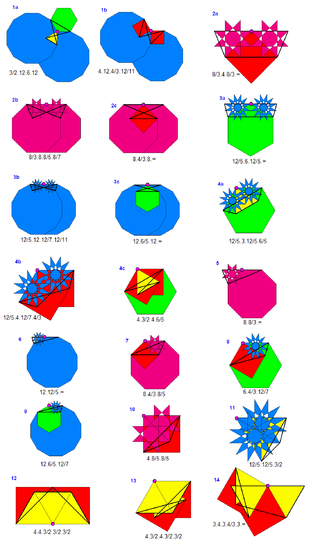The 21 grouped by shared edge graphs, given by vertex figures and Wythoff symbol, are:
Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, a uniform tiling is a tessellation
Tessellation
A tessellation or tiling of the plane is a pattern of plane figures that fills the plane with no overlaps and no gaps. One may also speak of tessellations of parts of the plane or of other surfaces. Generalizations to higher dimensions are also possible. Tessellations frequently appeared in the art...
of the plane by regular polygon
Regular polygon
A regular polygon is a polygon that is equiangular and equilateral . Regular polygons may be convex or star.-General properties:...
faces with the restriction of being vertex-uniform.
Uniform tilings can exist in both the Euclidean plane and hyperbolic plane
Hyperbolic space
In mathematics, hyperbolic space is a type of non-Euclidean geometry. Whereas spherical geometry has a constant positive curvature, hyperbolic geometry has a negative curvature: every point in hyperbolic space is a saddle point...
. Uniform tilings are related to the finite uniform polyhedra
Uniform polyhedron
A uniform polyhedron is a polyhedron which has regular polygons as faces and is vertex-transitive...
which can be considered uniform tilings of the sphere.
Most uniform tilings can be made from a Wythoff construction
Wythoff construction
In geometry, a Wythoff construction, named after mathematician Willem Abraham Wythoff, is a method for constructing a uniform polyhedron or plane tiling. It is often referred to as Wythoff's kaleidoscopic construction.- Construction process :...
starting with a symmetry group
Symmetry group
The symmetry group of an object is the group of all isometries under which it is invariant with composition as the operation...
and a singular generator point inside of the fundamental domain. A planar symmetry group has a polygonal fundamental domain
Fundamental domain
In geometry, the fundamental domain of a symmetry group of an object is a part or pattern, as small or irredundant as possible, which determines the whole object based on the symmetry. More rigorously, given a topological space and a group acting on it, the images of a single point under the group...
and can be represented by the group name represented by the order of the mirrors in sequential vertices.
A fundamental domain triangle is (p q r), and a right triangle (p q 2), where p, q, r are whole numbers greater than 1. The triangle may exist as a spherical triangle, an Euclidean plane triangle, or a hyperbolic plane triangle, depending on the values of p, q and r.
There are a number of symbolic schemes for naming these figures, from a modified Schläfli symbol for right triangle domains: (p q 2) --> {p, q}. The Coxeter-Dynkin diagram
Coxeter-Dynkin diagram
In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors...
is a triangular graph with p, q, r labeled on the edges. If r = 2, the graph is linear since order-2 domain nodes generate no reflections. The Wythoff symbol
Wythoff symbol
In geometry, the Wythoff symbol was first used by Coxeter, Longeut-Higgens and Miller in their enumeration of the uniform polyhedra. It represents a construction by way of Wythoff's construction applied to Schwarz triangles....
takes the 3 integers and separates them by a vertical bar (|). If the generator point is off the mirror opposite a domain node, it is given before the bar.
Finally tilings can be described by their vertex configuration
Vertex configuration
In geometry, a vertex configuration is a short-hand notation for representing the vertex figure of a polyhedron or tiling as the sequence of faces around a vertex. For uniform polyhedra there is only one vertex type and therefore the vertex configuration fully defines the polyhedron...
, the sequence of polygons around each vertex.
All uniform tilings can be constructed from various operations applied to regular tilings. These operations as named by Norman Johnson are called truncation
Truncation (geometry)
In geometry, a truncation is an operation in any dimension that cuts polytope vertices, creating a new facet in place of each vertex.- Uniform truncation :...
(cutting vertices), rectification
Rectification (geometry)
In Euclidean geometry, rectification is the process of truncating a polytope by marking the midpoints of all its edges, and cutting off its vertices at those points...
(cutting vertices until edges disappear), and Cantellation (cutting edges). Omnitruncation is an operation that combines truncation and cantellation. Snubbing is an operation of Alternate truncation of the omnitruncated form. (See Uniform polyhedron#Wythoff construction operators for more details.)
Coxeter groups
Coxeter groupCoxeter group
In mathematics, a Coxeter group, named after H.S.M. Coxeter, is an abstract group that admits a formal description in terms of mirror symmetries. Indeed, the finite Coxeter groups are precisely the finite Euclidean reflection groups; the symmetry groups of regular polyhedra are an example...
s for the plane define the Wythoff construction and can be represented by Coxeter-Dynkin diagram
Coxeter-Dynkin diagram
In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors...
s:
For groups with whole number orders, including:
| Orbifold symmetry |
Coxeter group Coxeter group In mathematics, a Coxeter group, named after H.S.M. Coxeter, is an abstract group that admits a formal description in terms of mirror symmetries. Indeed, the finite Coxeter groups are precisely the finite Euclidean reflection groups; the symmetry groups of regular polyhedra are an example... |
Coxeter-Dynkin diagram Coxeter-Dynkin diagram In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors... |
notes | ||
|---|---|---|---|---|---|
| Compact | |||||
| *333 | (3 3 3) |  |
[Δ] | 3 reflective forms, 1 snub | |
| *442 | (4 4 2) |  |
[4,4] | 5 reflective forms, 1 snub | |
| *632 | (6 3 2) |  |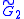
[6,3] | 7 reflective forms, 1 snub | |
| *2222 | (∞ 2 ∞ 2) |  ×  |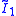
[∞] × [∞] | 3 reflective forms, 1 snub | |
| Noncompact | |||||
| *∞∞ | (∞) |  |
[∞] | ||
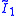| *22∞ | (2 2 ∞) |  ×  |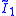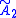
[∞] × [ ] | 2 reflective forms, 1 snub | |
| Orbifold symmetry |
Coxeter group Coxeter group In mathematics, a Coxeter group, named after H.S.M. Coxeter, is an abstract group that admits a formal description in terms of mirror symmetries. Indeed, the finite Coxeter groups are precisely the finite Euclidean reflection groups; the symmetry groups of regular polyhedra are an example... |
Coxeter-Dynkin diagram Coxeter-Dynkin diagram In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors... |
notes | |
|---|---|---|---|---|
| Compact | ||||
| *pq2 | (p q 2) | [p,q] | 2p+2q < pq | |
| *pqr | (p q r) | pq+pr+qr < pqr | ||
| Noncompact | ||||
| *∞p2 | (p ∞ 2) | [p,∞] | p>=3 | |
| *∞pq | (p q ∞) | p,q>=3, p+q>6 | ||
| *∞∞p | (p ∞ ∞) | p>=3 | ||
| *∞∞∞ | (∞ ∞ ∞) | |||
Uniform tilings of the Euclidean plane
There are symmetry groups on the Euclidean plane constructed from fundamental triangles: (4 4 2), (6 3 2), and (3 3 3). Each is represented by a set of lines of reflection that divide the plane into fundamental triangles.These symmetry groups create 3 regular tilings, and 7 semiregular ones. A number of the semiregular tilings are repeated from different symmetry constructors.
A prismatic symmetry group represented by (2 2 2 2) represents by two sets of parallel mirrors, which in general can have a rectangular fundamental domain. It generates no new tilings.
A further prismatic symmetry group represented by (∞ 2 2) which has an infinite fundamental domain. It constructs two uniform tilings, the apeirogonal prism
Apeirogonal prism
In geometry, an apeirogonal prism or infinite prism is the arithmetic limit of the family of prisms; it can be considered an infinite polyhedron or a tiling of the plane....
and apeirogonal antiprism
Apeirogonal antiprism
In geometry, an apeirogonal antiprism or infinite antiprism is the arithmetic limit of the family of antiprisms; it can be considered an infinite polyhedron or a tiling of the plane.If the sides are equilateral triangles, it is a uniform tiling...
.
The stacking of the finite faces of these two prismatic tilings constructs one non-Wythoffian uniform tiling of the plane. It is called the elongated triangular tiling
Elongated triangular tiling
In geometry, the elongated triangular tiling is a semiregular tiling of the Euclidean plane. There are three triangles and two squares on each vertex.Conway calls it a isosnub quadrille....
, composed of alternating layers of squares and triangles.
Right angle fundamental triangles: (p q 2)
| (p q 2) | Fund. triangles |
Parent | Truncated | Rectified | Bitruncated | Birectified (dual) |
Cantellated | Omnitruncated (Cantitruncated) |
Snub |
|---|---|---|---|---|---|---|---|---|---|
| Wythoff symbol Wythoff construction In geometry, a Wythoff construction, named after mathematician Willem Abraham Wythoff, is a method for constructing a uniform polyhedron or plane tiling. It is often referred to as Wythoff's kaleidoscopic construction.- Construction process :... |
q | p 2 | 2 q | p | 2 | p q | 2 p | q | p | q 2 | p q | 2 | p q 2 | | | p q 2 | |
| Schläfli symbol | t0{p,q} | t0,1{p,q} | t1{p,q} | t1,2{p,q} | t2{p,q} | t0,2{p,q} | t0,1,2{p,q} | s{p,q} | |
| Coxeter-Dynkin diagram Coxeter-Dynkin diagram In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors... |
|||||||||
| Vertex figure Vertex configuration In geometry, a vertex configuration is a short-hand notation for representing the vertex figure of a polyhedron or tiling as the sequence of faces around a vertex. For uniform polyhedra there is only one vertex type and therefore the vertex configuration fully defines the polyhedron... |
pq | (q.2p.2p) | (p.q.p.q) | (p.2q.2q) | qp | (p.4.q.4) | (4.2p.2q) | (3.3.p.3.q) | |
| Square tiling (4 4 2) |
 V4.8.8 |
 {4,4} |
 4.8.8 Truncated square tiling In geometry, the truncated square tiling is a semiregular tiling of the Euclidean plane. There is one square and two octagons on each vertex. This is the only edge-to-edge tiling by regular convex polygons which contains an octagon... |
 4.4.4.4 |
 4.8.8 Truncated square tiling In geometry, the truncated square tiling is a semiregular tiling of the Euclidean plane. There is one square and two octagons on each vertex. This is the only edge-to-edge tiling by regular convex polygons which contains an octagon... |
 {4,4} |
 4.4.4.4 |
 4.8.8 Truncated square tiling In geometry, the truncated square tiling is a semiregular tiling of the Euclidean plane. There is one square and two octagons on each vertex. This is the only edge-to-edge tiling by regular convex polygons which contains an octagon... |
 3.3.4.3.4 |
| Hexagonal tiling (6 3 2) |
 V4.6.12 |
 {6,3} |
 3.12.12 Truncated hexagonal tiling In geometry, the truncated hexagonal tiling is a semiregular tiling of the Euclidean plane. There are 2 dodecagons and one triangle on each vertex.... |
 3.6.3.6 Trihexagonal tiling In geometry, the trihexagonal tiling is a semiregular tiling of the Euclidean plane. There are two triangles and two hexagons alternating on each vertex... |
 6.6.6 |
 {3,6} |
 3.4.6.4 |
 4.6.12 Great rhombitrihexagonal tiling In geometry, the truncated trihexagonal tiling is a semiregular tiling of the Euclidean plane. There are one square, one hexagon, and one dodecagon on each vertex... |
 3.3.3.3.6 Snub hexagonal tiling In geometry, the Snub hexagonal tiling is a semiregular tiling of the Euclidean plane. There are four triangles and one hexagon on each vertex... |
General fundamental triangles: (p q r)
| Wythoff symbol Wythoff construction In geometry, a Wythoff construction, named after mathematician Willem Abraham Wythoff, is a method for constructing a uniform polyhedron or plane tiling. It is often referred to as Wythoff's kaleidoscopic construction.- Construction process :... (p q r) |
Fund. triangles |
q | p r | r q | p | r | p q | r p | q | p | q r | p q | r | p q r | | | p q r |
|---|---|---|---|---|---|---|---|---|---|
| Coxeter-Dynkin diagram Coxeter-Dynkin diagram In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors... |
|||||||||
| Vertex figure Vertex configuration In geometry, a vertex configuration is a short-hand notation for representing the vertex figure of a polyhedron or tiling as the sequence of faces around a vertex. For uniform polyhedra there is only one vertex type and therefore the vertex configuration fully defines the polyhedron... |
(p.q)r | (r.2p.q.2p) | (p.r)q | (q.2r.p.2r) | (q.r)p | (q.2r.p.2r) | (r.2q.p.2q) | (3.r.3.q.3.p) | |
| Triangular (3 3 3) |
V6.6.6 |
 (3.3)3 |
 3.6.3.6 Trihexagonal tiling In geometry, the trihexagonal tiling is a semiregular tiling of the Euclidean plane. There are two triangles and two hexagons alternating on each vertex... |
 (3.3)3 |
 3.6.3.6 Trihexagonal tiling In geometry, the trihexagonal tiling is a semiregular tiling of the Euclidean plane. There are two triangles and two hexagons alternating on each vertex... |
 (3.3)3 |
 3.6.3.6 Trihexagonal tiling In geometry, the trihexagonal tiling is a semiregular tiling of the Euclidean plane. There are two triangles and two hexagons alternating on each vertex... |
 6.6.6 |
 3.3.3.3.3.3 |
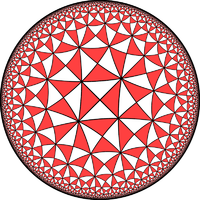
Uniform tilings of the hyperbolic plane
There are infinitely many uniform tilings of convex regular polygons on the hyperbolic planeHyperbolic space
In mathematics, hyperbolic space is a type of non-Euclidean geometry. Whereas spherical geometry has a constant positive curvature, hyperbolic geometry has a negative curvature: every point in hyperbolic space is a saddle point...
, each based on a different reflective symmetry group (p q r).
A sampling is shown here with a Poincaré disk
Poincaré disk model
In geometry, the Poincaré disk model, also called the conformal disk model, is a model of n-dimensional hyperbolic geometry in which the points of the geometry are in an n-dimensional disk, or unit ball, and the straight lines of the hyperbolic geometry are segments of circles contained in the disk...
projection.
The Coxeter-Dynkin diagram
Coxeter-Dynkin diagram
In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors...
is given in a linear form, although it is actually a triangle, with the trailing segment r connecting to the first node.
Further Symmetry groups exist in the hyperbolic plane with quadrilateral fundamental domains starting with (2 2 2 3), etc, that can generate new forms. As well there's fundamental domains that place vertices at infinity, such as (∞ 2 3), etc.
Right angle fundamental triangles: (p q 2)
| (p q 2) | Fund. triangles |
Parent | Truncated | Rectified | Bitruncated | Birectified (dual) |
Cantellated | Omnitruncated (Cantitruncated) |
Snub |
|---|---|---|---|---|---|---|---|---|---|
| Wythoff symbol Wythoff construction In geometry, a Wythoff construction, named after mathematician Willem Abraham Wythoff, is a method for constructing a uniform polyhedron or plane tiling. It is often referred to as Wythoff's kaleidoscopic construction.- Construction process :... |
q | p 2 | 2 q | p | 2 | p q | 2 p | q | p | q 2 | p q | 2 | p q 2 | | | p q 2 | |
| Schläfli symbol | t0{p,q} | t0,1{p,q} | t1{p,q} | t1,2{p,q} | t2{p,q} | t0,2{p,q} | t0,1,2{p,q} | s{p,q} | |
| Coxeter-Dynkin diagram Coxeter-Dynkin diagram In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors... |
|||||||||
| Vertex figure Vertex configuration In geometry, a vertex configuration is a short-hand notation for representing the vertex figure of a polyhedron or tiling as the sequence of faces around a vertex. For uniform polyhedra there is only one vertex type and therefore the vertex configuration fully defines the polyhedron... |
pq | (q.2p.2p) | (p.q.p.q) | (p.2q.2q) | qp | (p.4.q.4) | (4.2p.2q) | (3.3.p.3.q) | |
| (Hyperbolic plane) (5 4 2) |
 |
 {5,4} |
 4.10.10 |
 4.5.4.5 |
 5.8.8 |
 {4,5} |
 4.4.5.4 |
 4.8.10 |
 3.3.4.3.5 |
| (Hyperbolic plane) (5 5 2) |
 |
 {5,5} |
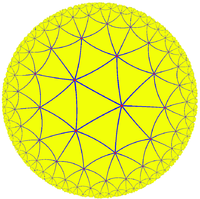
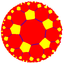 5.10.10 |
 5.5.5.5 |
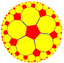 5.10.10 |
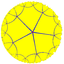 {5,5} |
 5.4.5.4 |
 4.10.10 |
 3.3.5.3.5 |
| (Hyperbolic plane) (7 3 2) |
 |
 {7,3} |
 3.14.14 |
 3.7.3.7 Triheptagonal tiling In geometry, the triheptagonal tiling is a semiregular tiling of the hyperbolic plane, representing a rectified Order-3 heptagonal tiling. There are two triangles and two heptagons alternating on each vertex... |
 7.6.6 |
 {3,7} |
 3.4.7.4 |
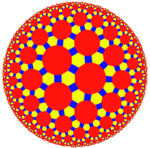 4.6.14 |
 3.3.3.3.7 |
| (Hyperbolic plane) (8 3 2) |
 |
 {8,3} |
 3.16.16 |
 3.8.3.8 |
 8.6.6 |
 {3,8} |
 3.4.8.4 |
 4.6.16 |
 3.3.3.3.8 |
General fundamental triangles (p q r)
| Wythoff symbol Wythoff construction In geometry, a Wythoff construction, named after mathematician Willem Abraham Wythoff, is a method for constructing a uniform polyhedron or plane tiling. It is often referred to as Wythoff's kaleidoscopic construction.- Construction process :... (p q r) |
Fund. triangles |
q | p r | r q | p | r | p q | r p | q | p | q r | p q | r | p q r | | | p q r |
|---|---|---|---|---|---|---|---|---|---|
| Coxeter-Dynkin diagram Coxeter-Dynkin diagram In geometry, a Coxeter–Dynkin diagram is a graph with numerically labeled edges representing the spatial relations between a collection of mirrors... |
|||||||||
| Vertex figure Vertex configuration In geometry, a vertex configuration is a short-hand notation for representing the vertex figure of a polyhedron or tiling as the sequence of faces around a vertex. For uniform polyhedra there is only one vertex type and therefore the vertex configuration fully defines the polyhedron... |
(p.r)q | (r.2p.q.2p) | (p.q)r | (q.2r.p.2r) | (q.r)p | (q.2r.p.2r) | (r.2q.p.2q) | (3.r.3.q.3.p) | |
| Hyperbolic (4 3 3) |
 |
 (3.4)3 |
 3.8.3.8 |
 (3.4)3 |
 3.6.4.6 |
 (3.3)4 |
 3.6.4.6 |
 6.6.8 |
 3.3.3.3.3.4 |
| Hyperbolic (4 4 3) |
 |
 (3.4)4 |
 3.8.4.8 |
 (4.4)3 |
 3.6.4.6 |
 (3.4)4 |
 4.6.4.6 |
 6.8.8 |
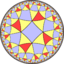 3.3.3.4.3.4 |
| Hyperbolic (4 4 4) |
 |
 (4.4)4 |
 4.8.4.8 |
 (4.4)4 |
 4.8.4.8 |
 (4.4)4 |
 4.8.4.8 |
 8.8.8 |
 3.4.3.4.3.4 |
Expanded lists of uniform tilings
There are a number ways the list of uniform tilings can be expanded:- Vertex figures can have retrograde faces and turn around the vertex more than once.
- Star polygons tiles can be included.
- ApeirogonApeirogonAn apeirogon is a degenerate polygon with a countably infinite number of sides. It is the limit of a sequence of polygons with more and more sides.Like any polygon, it is a sequence of line segments and angles...
s, {∞}, can be used as tiling faces. - The restriction that tiles meet edge-to-edge can be relaxed, allowing additional tilings such as the Pythagorean tilingPythagorean tilingIn geometry, the Pythagorean tiling or two squares tessellation is a tessellation of the plane by squares of two different sizes, in which each square touches four squares of the other size on its four sides. A tiling of this type may be formed by squares of any two different sizes...
.
Symmetry group triangles with retrogrades include:
- (4/3 4/3 2) (6 3/2 2) (6/5 3 2) (6 6/5 3) (6 6 3/2)
Symmetry group triangles with infinity include:
- (4 4/3 ∞) (3/2 3 ∞) (6 6/5 ∞) (3 3/2 ∞)
Branko Grünbaum
Branko Grünbaum
Branko Grünbaum is a Croatian-born mathematician and a professor emeritus at the University of Washington in Seattle. He received his Ph.D. in 1957 from Hebrew University of Jerusalem in Israel....
, in the 1987 book Tilings and patterns, in section 12.3 enumerates a list of 25 uniform tilings, including the 11 convex forms, and adds 14 more he calls hollow tilings which included the first two expansions above, star polygon faces and vertex figures.
H.S.M. Coxeter et al., in the 1954 paper 'Uniform polyhedra', in Table 8: Uniform Tessellations, uses all of these and enumerates a total of 38 uniform tilings.
Finally, if a tiling made of 2 apeirogons is also counted, the total can be considered 39 uniform tilings.
Vertex figure
In geometry a vertex figure is, broadly speaking, the figure exposed when a corner of a polyhedron or polytope is sliced off.-Definitions - theme and variations:...
and Wythoff symbol
Wythoff symbol
In geometry, the Wythoff symbol was first used by Coxeter, Longeut-Higgens and Miller in their enumeration of the uniform polyhedra. It represents a construction by way of Wythoff's construction applied to Schwarz triangles....
are:
- ∞.∞ (Two half-plane tiles, infinite dihedronDihedronA dihedron is a type of polyhedron, made of two polygon faces which share the same set of edges. In three-dimensional Euclidean space, it is degenerate if its faces are flat, while in three-dimensional spherical space, a dihedron with flat faces can be thought of as a lens, an example of which is...
) - 4.4.∞ - ∞ 2 | 2 (Apeirogonal prismApeirogonal prismIn geometry, an apeirogonal prism or infinite prism is the arithmetic limit of the family of prisms; it can be considered an infinite polyhedron or a tiling of the plane....
) - 3.3.3.∞ - | 2 2 ∞ (Apeirogonal antiprismApeirogonal antiprismIn geometry, an apeirogonal antiprism or infinite antiprism is the arithmetic limit of the family of antiprisms; it can be considered an infinite polyhedron or a tiling of the plane.If the sides are equilateral triangles, it is a uniform tiling...
) - 4.∞.4/3.∞ - 4/3 4 | ∞ (alternate square tiling)
- 3.∞.3.∞.3.∞ - 3/2 | 3 ∞ (alternate triangular tiling)
- 6.∞.6/5.∞ - 6/5 6 | ∞ (alternate trihexagonal tiling with only hexagons)
- ∞.3.∞.3/2 - 3/2 3 | ∞ (alternate trihexagonal tiling with only triangles)
The remaining list includes 21 tilings, 7 with {∞} tiles (apeirogons). Drawn as edge-graphs there are only 14 unique tilings, and the first is identical to the 3.4.6.4 tiling.
- Type 1
- 3/2.12.6.12 - 3/2 6 | 6
- 4.12.4/3.12/11 - 2 6 (3/2 3) |
- Type 2
- 8/3.4.8/3.∞ - 4 ∞ | 4/3
- 8/3.8.8/5.8/7 - 4/3 4 (2 ∞) |
- 8.4/3.8.∞ - 4/3 ∞ | 4
- Type 3
- 12/5.6.12/5.∞ - 6 ∞ | 6/5
- 12/5.12.12/7.12/11 - 6/5 6 (3 ∞) |
- 12.6/5.12.∞ - 6/5 ∞ | 6
- Type 4
- 12/5.3.12/5.6/5 - 3 6 | 6/5
- 12/5.4.12/7.4/3 - 2 6/5 (3/2 3) |
- 4.3/2.4.6/5 - 3/2 6 | 2
- Type 5
- 8.8/3.∞ - 4/3 4 ∞ |
- Type 6
- 12.12/5.∞ - 6/5 6 ∞ |
- Type 7
- 8.4/3.8/5 - 2 4/3 4 |
- Type 8
- 6.4/3.12/7 - 2 3 6/5 |
- Type 9
- 12.6/5.12/7 - 3 6/5 6 |
- Type 10
- 4.8/5.8/5 - 2 4 | 4/3
- Type 11
- 12/5.12/5.3/2 - 2 3 | 6/5
- Type 12
- 4.4.3/2.3/2.3/2 - non-Wythoffian
- Type 13
- 4.3/2.4.3/2.3/2 - | 2 4/3 4/3 (snub)
- Type 14
- 3.4.3.4/3.3.∞ - | 4/3 4 ∞ (snub)
Self-dual tilings
Tilings can also be self-dual. The square tiling with Schlafli symbols {4,4} is self-dual.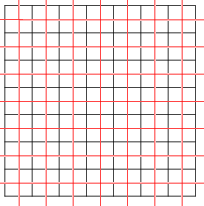 The {4,4} square tiling (black) with its dual (red). |
See also
- Uniform tessellationUniform tessellationIn geometry, a uniform tessellation is a vertex-transitive tessellations made from uniform polytope facets. All of its vertices are identical and there is the same combination and arrangement of faces at each vertex....
- Wythoff symbolWythoff symbolIn geometry, the Wythoff symbol was first used by Coxeter, Longeut-Higgens and Miller in their enumeration of the uniform polyhedra. It represents a construction by way of Wythoff's construction applied to Schwarz triangles....
- List of uniform tilings
- Uniform tilings in hyperbolic planeUniform tilings in hyperbolic planeThere are an infinite number of uniform tilings on the hyperbolic plane based on the where 1/p + 1/q + 1/r ...
- Uniform polytopeUniform polytopeA uniform polytope is a vertex-transitive polytope made from uniform polytope facets of a lower dimension. Uniform polytopes of 2 dimensions are the regular polygons....