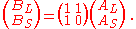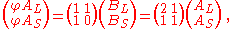Penrose tiling - AbsoluteAstronomy.com

A Penrose tiling is a non-periodic tiling

Tessellation

A tessellation or tiling of the plane is a pattern of plane figures that fills the plane with no overlaps and no gaps. One may also speak of tessellations of parts of the plane or of other surfaces. Generalizations to higher dimensions are also possible. Tessellations frequently appeared in the art...

generated by an aperiodic set

Aperiodic tiling

An aperiodic tiling is a tiling obtained from an aperiodic set of tiles. Properly speaking, aperiodicity is a property of particular sets of tiles; any given finite tiling is either periodic or non-periodic...

of prototile

Prototile

In the mathematical theory of tessellations, a prototile is one of the shapes of a tile in a tessellation.A tessellation of the plane or of any other space is a cover of the space by closed shapes, called tiles, that have disjoint interiors. Some of the tiles may be congruent to one or more others...

s named after Sir Roger Penrose

Roger Penrose

Sir Roger Penrose OM FRS is an English mathematical physicist and Emeritus Rouse Ball Professor of Mathematics at the Mathematical Institute, University of Oxford and Emeritus Fellow of Wadham College...

, who investigated these sets in the 1970s. The aperiodicity of the Penrose prototiles implies that a shifted copy of a Penrose tiling will never match the original. A Penrose tiling may be constructed so as to exhibit both reflection symmetry

Reflection symmetry

Reflection symmetry, reflectional symmetry, line symmetry, mirror symmetry, mirror-image symmetry, or bilateral symmetry is symmetry with respect to reflection. That is, a figure which does not change upon undergoing a reflection has reflectional symmetry.In 2D there is a line of symmetry, in 3D a...

and fivefold rotational symmetry

Rotational symmetry

Generally speaking, an object with rotational symmetry is an object that looks the same after a certain amount of rotation. An object may have more than one rotational symmetry; for instance, if reflections or turning it over are not counted, the triskelion appearing on the Isle of Man's flag has...

, as in the diagram at the right.

A Penrose tiling has many remarkable properties, most notably:

It is non-periodic, which means that it lacks any translational symmetry
Translational symmetry
In geometry, a translation "slides" an object by a a: Ta = p + a.In physics and mathematics, continuous translational symmetry is the invariance of a system of equations under any translation...

. More informally, a shifted copy will never match the original.
It is self-similar
Self-similarity
In mathematics, a self-similar object is exactly or approximately similar to a part of itself . Many objects in the real world, such as coastlines, are statistically self-similar: parts of them show the same statistical properties at many scales...

, so the same patterns occur at larger and larger scales. Thus, the tiling can be obtained through "inflation" (or "deflation") and any finite patch from the tiling occurs infinitely many times.
It is a quasicrystal
Quasicrystal
A quasiperiodic crystal, or, in short, quasicrystal, is a structure that is ordered but not periodic. A quasicrystalline pattern can continuously fill all available space, but it lacks translational symmetry...

: implemented as a physical structure a Penrose tiling will produce Bragg diffraction and its diffractogram reveals both the fivefold symmetry and the underlying long range order.

Various methods to construct Penrose tilings have been discovered, including matching rules, substitutions, cut and project schemes and coverings.

Periodic and aperiodic tilings

Penrose tilings are simple examples of aperiodic tiling

Aperiodic tiling

s of the plane. A tiling

Tessellation

is a covering of the plane by tiles with no overlaps or gaps; the tiles normally have a finite number of shapes, called prototile
Prototile
In the mathematical theory of tessellations, a prototile is one of the shapes of a tile in a tessellation.A tessellation of the plane or of any other space is a cover of the space by closed shapes, called tiles, that have disjoint interiors. Some of the tiles may be congruent to one or more others...

s, and a set of prototiles is said to admit a tiling or tile the plane if there is a tiling of the plane using only tiles congruent

Congruence (geometry)

In geometry, two figures are congruent if they have the same shape and size. This means that either object can be repositioned so as to coincide precisely with the other object...

to these prototiles. The most familiar tilings (e.g., by squares or triangles) are periodic: a perfect copy of the tiling can be obtained by translating all of the tiles by a fixed distance in a given direction. Such a translation is called a period of the tiling; more informally, this means that a finite region of the tiling repeats itself in periodic intervals. If a tiling has no periods it is said to be non-periodic. A set of prototiles is said to be aperiodic if it tiles the plane, but every such tiling is non-periodic; tilings by aperiodic sets of prototiles are called aperiodic tilings.

Earliest aperiodic tilings

The subject of aperiodic tilings received new interest in the 1960s when logician Hao Wang noted connections between decision problem

Decision problem

In computability theory and computational complexity theory, a decision problem is a question in some formal system with a yes-or-no answer, depending on the values of some input parameters. For example, the problem "given two numbers x and y, does x evenly divide y?" is a decision problem...

s and tilings. In particular, he introduced tilings by square plates with colored edges, now known as Wang dominoes or tiles, and posed the "Domino Problem
Domino problem
In geometry, the domino problem is the problem of deciding whether a set of tiles of a particular kind admits a tiling.In a 1961 paper proposing a method for deciding an important case of David Hilbert's Entscheidungsproblem, the logician Hao Wang discussed tiling the plane by equally sized square...

": to determine whether a given set of Wang dominoes could tile the plane with matching colors on adjacent domino edges. He observed that if this problem were undecidable

Recursive set

In computability theory, a set of natural numbers is called recursive, computable or decidable if there is an algorithm which terminates after a finite amount of time and correctly decides whether or not a given number belongs to the set....

, then there would have to exist an aperiodic set of Wang dominoes. At the time, this seemed implausible, so Wang conjectured no such set could exist.

Wang's student Robert Berger

Robert Berger (mathematician)

Robert Berger is known for inventing the first aperiodic tiling using a set of 20,426 distinct tile shapes.The unexpected existence of aperiodic tilings, although not Berger's explicit construction of them, follows from another result proved by Berger: that the so-called domino problem is...

proved that the Domino Problem was undecidable (so Wang's conjecture was false) in his 1964 thesis, and obtained an aperiodic set of 20426 Wang dominoes. He also described a reduction to 104 such prototiles; the latter did not appear in his published monograph, but in 1968, Donald Knuth

Donald Knuth

Donald Ervin Knuth is a computer scientist and Professor Emeritus at Stanford University.He is the author of the seminal multi-volume work The Art of Computer Programming. Knuth has been called the "father" of the analysis of algorithms...

detailed a modification of Berger's set requiring only 92 dominoes.

The color matching required in a tiling by Wang dominoes can easily be achieved by modifying the edges of the tiles like jigsaw puzzle

Jigsaw puzzle

A jigsaw puzzle is a tiling puzzle that requires the assembly of numerous small, often oddly shaped, interlocking and tessellating pieces.Each piece usually has a small part of a picture on it; when complete, a jigsaw puzzle produces a complete picture...

pieces so that they can fit together only as prescribed by the edge colorings. Raphael Robinson, in a 1971 paper which simplified Berger's techniques and undecidability proof, used this technique to obtain an aperiodic set of just six prototiles.

Development of the Penrose tilings

The first Penrose tiling (tiling P1 below) is also an aperiodic set of six prototiles, introduced by Roger Penrose

Roger Penrose

in a 1974 paper, but is based on pentagons rather than squares. Any attempts to tile the plane with regular pentagons will necessarily leave gaps, but Johannes Kepler

Johannes Kepler

Johannes Kepler was a German mathematician, astronomer and astrologer. A key figure in the 17th century scientific revolution, he is best known for his eponymous laws of planetary motion, codified by later astronomers, based on his works Astronomia nova, Harmonices Mundi, and Epitome of Copernican...

showed, in his 1619 work Harmonices Mundi, that these gaps could be filled using pentagram

Pentagram

A pentagram is the shape of a five-pointed star drawn with five straight strokes...

s (viewed as star polygons), decagon

Decagon

In geometry, a decagon is any polygon with ten sides and ten angles, and usually refers to a regular decagon, having all sides of equal length and each internal angle equal to 144°...

s and related shapes. Acknowledging inspiration from Kepler, Penrose was able to find matching rules (which can be imposed by decorations of the edges) for these shapes, in order to obtain an aperiodic set; his tiling can be viewed as a completion of Kepler's finite Aa pattern, and other traces of these ideas can be found in Albrecht Dürer

Albrecht Dürer

Albrecht Dürer was a German painter, printmaker, engraver, mathematician, and theorist from Nuremberg. His prints established his reputation across Europe when he was still in his twenties, and he has been conventionally regarded as the greatest artist of the Northern Renaissance ever since...

's work.

Penrose subsequently reduced the number of prototiles to two, discovering the kite and dart tiling (tiling P2 below) and the rhombus tiling (tiling P3 below). The rhombus tiling was independently discovered by Robert Ammann

Robert Ammann

Robert Ammann was an amateur mathematician who made several significant and groundbreaking contributions to the theory of quasicrystals and aperiodic tilings....

in 1976. Penrose and John H. Conway investigated the properties of Penrose tilings, and discovered that a substitution property explained their hierarchical nature; their findings were publicized by Martin Gardner

Martin Gardner

Martin Gardner was an American mathematics and science writer specializing in recreational mathematics, but with interests encompassing micromagic, stage magic, literature , philosophy, scientific skepticism, and religion...

in his January 1977 "Mathematical Games" column in Scientific American
Scientific American
Scientific American is a popular science magazine. It is notable for its long history of presenting science monthly to an educated but not necessarily scientific public, through its careful attention to the clarity of its text as well as the quality of its specially commissioned color graphics...

.

In 1981, De Bruijn

Nicolaas Govert de Bruijn

Nicolaas Govert de Bruijn is a Dutch mathematician, affiliated as professor emeritus with the Eindhoven University of Technology. He received his Ph.D. in 1943 from Vrije Universiteit Amsterdam....

explained a method to construct Penrose tilings from five families of parallel lines as well as a "cut and project method", in which Penrose tilings are obtained as two-dimensional projections from a five-dimensional cubic structure. In this approach, the Penrose tiling is viewed as a set of points, its vertices, while the tiles are geometrical shapes obtained by connecting vertices with edges.

The Penrose tilings

The three types of Penrose tiling P1–P3 are described individually below. They have many common features: in each case, the tiles are constructed from shapes related to the pentagon (and hence to the golden ratio

Golden ratio

In mathematics and the arts, two quantities are in the golden ratio if the ratio of the sum of the quantities to the larger quantity is equal to the ratio of the larger quantity to the smaller one. The golden ratio is an irrational mathematical constant, approximately 1.61803398874989...

), but the basic tile shapes need to be supplemented by matching rules in order to tile aperiodically; these rules may be described using labeled vertices or edges, or patterns on the tile faces – alternatively the edge profile can be modified (e.g. by indentations and protrusions) to obtain an aperiodic set of prototiles.

The original pentagonal Penrose tiling (P1)

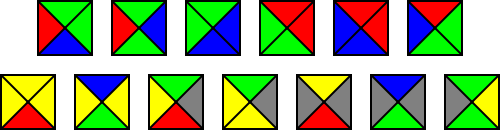
Penrose's first tiling uses pentagons and three other shapes: a five-pointed "star" (a pentagram), a "boat" (roughly 3/5 of a star) and a "diamond" (a thin rhombus). To ensure that all tilings are non-periodic, there are matching rules that specify how tiles may meet each other, and there are three different types of matching rule for the pentagonal tiles. It is common to indicate the three different types of pentagonal tiles using three different colors, as in the figure above right.

Kite and dart tiling (P2)

Penrose's second tiling uses quadrilaterals called the "kite" and "dart", which may be combined to make a rhombus. However, the matching rules prohibit such a combination. Both the kite and dart are composed of two triangles, called Robinson triangles, after 1975 notes by Robinson.

The kite is a quadrilateral whose four interior angles are 72, 72, 72, and 144 degrees. The kite may be bisected along its axis of symmetry to form a pair of acute Robinson triangles (with angles of 36, 72 and 72 degrees).
The dart is a non-convex quadrilateral whose four interior angles are 36, 72, 36, and 216 degrees. The dart may be bisected along its axis of symmetry to form a pair of obtuse Robinson triangles (with angles of 36, 36 and 108 degrees), which are smaller than the acute triangles.

The matching rules can be described in several ways. One approach is to color the vertices (with two colors, e.g., black and white) and require that adjacent tiles have matching vertices. Another is to use a pattern of circular arcs (as shown above left in green and red) to constrain the placement of tiles: when two tiles share an edge in a tiling, the patterns must match at these edges.

These rules often force the placement of certain tiles: for example, the concave vertex of any dart is necessarily filled by two kites. The corresponding figure (center of the top row in the lower image on the left) is called an "ace" by Conway; although it looks like an enlarged kite, it does not tile in the same way. Similarly the concave vertex formed when two kites meet along a short edge is necessarily filled by two darts (bottom right). In fact, there are only seven possible ways for the tiles to meet at a vertex; two of these figures – namely, the "star" (top left) and the "sun" (top right) – have 5-fold dihedral symmetry (by rotations and reflections), while the remainder have a single axis of reflection (vertical in the image). All of these vertex figures, apart from the ace and the sun, force the placement of additional tiles.

Rhombus tiling (P3)

The third tiling uses a pair of rhombus

Rhombus

In Euclidean geometry, a rhombus or rhomb is a convex quadrilateral whose four sides all have the same length. The rhombus is often called a diamond, after the diamonds suit in playing cards, or a lozenge, though the latter sometimes refers specifically to a rhombus with a 45° angle.Every...

es (often referred to as "rhombs" in this context) with equal sides but different angles. Ordinary rhombus-shaped tiles can be used to tile the plane periodically, so restrictions must be made on how tiles can be assembled: no two tiles may form a parallelogram, as this would allow a periodic tiling, but this constraint is not sufficient to force aperiodicity, as figure 1 above shows.

There are two kinds of tile, both of which can be decomposed into Robinson triangles.

The thin rhomb t has four corners with angles of 36, 144, 36, and 144 degrees. The t rhomb may be bisected along its short diagonal to form a pair of acute Robinson triangles.
The thick rhomb T has angles of 72, 108, 72, and 108 degrees. The T rhomb may be bisected along its long diagonal to form a pair of obtuse Robinson triangles; in contrast to the P2 tiling, these are larger than the acute triangles.

The matching rules distinguish sides of the tiles, and entail that tiles may be juxtaposed in certain particular ways but not in others. Two ways to describe these matching rules are shown in the image on the right. In one form, tiles must be assembled such that the curves on the faces match in color and position across an edge. In the other, tiles must be assembled such that the bumps on their edges fit together.

There are 54 cyclically ordered combinations of such angles that add up to 360 degrees at a vertex, but the rules of the tiling allow only seven of these combinations to appear (although one of these arises in two ways).

The golden ratio and local pentagonal symmetry

Several properties and common features of the Penrose tilings involve the golden ratio

Golden ratio

φ = (1+√5)/2 (approximately 1.618). This is the ratio of chord

Chord (geometry)

A chord of a circle is a geometric line segment whose endpoints both lie on the circumference of the circle.A secant or a secant line is the line extension of a chord. More generally, a chord is a line segment joining two points on any curve, such as but not limited to an ellipse...

lengths to side lengths in a regular pentagon, and satisfies φ = 1 + 1/φ.
Consequently, the ratio of the lengths of long sides to short sides in the (isosceles) Robinson triangles is φ:1. It follows that the ratio of long side lengths to short in both kite and dart tiles is also φ:1, as are the length ratios of sides to the short diagonal in the thin rhomb t, and of long diagonal to sides in the thick rhomb T. In both the P2 and P3 tilings, the ratio of the area of the larger Robinson triangle to the smaller one is φ:1, hence so are the ratios of the areas of the kite to the dart, and of the thick rhomb to the thin rhomb. (Both larger and smaller obtuse Robinson triangles can be found in the pentagon on the right: the larger triangles at the top – the halves of the thick rhomb – have linear dimensions scaled up by φ compared to the small shaded triangle at the base, and so the ratio of areas is φ²:1.)

Any Penrose tiling has local pentagonal symmetry, in the sense that there are points in the tiling surrounded by a symmetric configuration of tiles: such configurations have fivefold rotational symmetry

Rotational symmetry

about the center point, as well as five mirror lines of reflection symmetry

Reflection symmetry

passing through the point, a dihedral

Dihedral group

In mathematics, a dihedral group is the group of symmetries of a regular polygon, including both rotations and reflections. Dihedral groups are among the simplest examples of finite groups, and they play an important role in group theory, geometry, and chemistry.See also: Dihedral symmetry in three...

symmetry group

Group (mathematics)

In mathematics, a group is an algebraic structure consisting of a set together with an operation that combines any two of its elements to form a third element. To qualify as a group, the set and the operation must satisfy a few conditions called group axioms, namely closure, associativity, identity...

. This symmetry will generally preserve only a patch of tiles around the center point, but the patch can be very large: Conway and Penrose proved that whenever the colored curves on the P2 or P3 tilings close in a loop, the region within the loop has pentagonal symmetry, and furthermore, in any tiling, there are at most two such curves of each color which do not close up.

There can be at most one center point of global fivefold symmetry: if there were more than one, then rotating each about the other would yield two closer centers of fivefold symmetry, which leads to a mathematical contradiction. There are only two Penrose tilings (of each type) with global pentagonal symmetry: for the P2 tiling by kites and darts, the center point is either a "sun" or "star" vertex.

Inflation and deflation

Many of the common features of Penrose tilings follow from a hierarchical pentagonal structure given by substitution rules
Substitution tiling
In geometry, a tile substitution is a useful method for constructing highly ordered tilings. Most importantly, some tile substitutions generate aperiodic tilings, which are tilings whose prototiles do not admit any tiling with translational symmetry...

: this is often referred to as inflation and deflation, or composition and decomposition, of tilings or (collections of) tiles. The substitution rules decompose each tile into smaller tiles of the same shape as those used in the tiling (and thus allow larger tiles to be "composed" from smaller ones). This shows that the Penrose tiling has a scaling self-similarity, and so can be thought of as a fractal.

Penrose originally discovered the P1 tiling in this way, by decomposing a pentagon into six smaller pentagons (one half of a net

Net (polyhedron)

In geometry the net of a polyhedron is an arrangement of edge-joined polygons in the plane which can be folded to become the faces of the polyhedron...

of a dodecahedron) and five half-diamonds; he then observed that when he repeated this process the gaps between pentagons could all be filled by stars, diamonds, boats and other pentagons. By iterating this process indefinitely he obtained one of the two P1 tilings with pentagonal symmetry.

Robinson triangle decompositions

The substitution method for both P2 and P3 tilings can be described using Robinson triangles of different sizes. The Robinson triangles arising in P2 tilings (by bisecting kites and darts) are called A-tiles, while those arising in the P3 tilings (by bisecting rhombs) are called B-tiles. The smaller A-tile, denoted A_S, is an obtuse Robinson triangle, while the larger A-tile, A_L, is acute; in contrast, a smaller B-tile, denoted B_S, is an acute Robinson triangle, while the larger B-tile, B_L, is obtuse.

Concretely, if A_S has side lengths (1, 1, φ), then A_L has side lengths (φ, φ, 1). B-tiles can be related to such A-tiles in two ways:

If B_S has the same size as A_L then B_L is an enlarged version φA_S of A_S, with side lengths (φ, φ, φ²=1+φ) – this decomposes into an A_L tile and A_S tile joined along a common side of length 1.
If instead B_L is identified with A_S, then B_S is a reduced version (1/φ)A_L of A_L with side lengths (1/φ,1/φ,1) – joining a B_S tile and a B_L tile along a common side of length 1 then yields (a decomposition of) an A_L tile.

In these decompositions, there appears to be an ambiguity: Robinson triangles may be decomposed in two ways, which are mirror images of each other in the (isosceles) axis of symmetry of the triangle. In a Penrose tiling, this choice is fixed by the matching rules – furthermore, the matching rules also determine how the smaller triangles in the tiling compose to give larger ones.
It follows that the P2 and P3 tilings are mutually locally derivable: a tiling by one set of tiles can be used to generate a tiling by another – for example a tiling by kites and darts may be subdivided into A-tiles, and these can be composed in a canonical way to form B-tiles and hence rhombs. The P2 and P3 tilings are also both mutually locally derivable with the P1 tiling (see figure 2 above).

The decomposition of B-tiles into A-tiles may be written

B_S = A_L, B_L = A_L + A_S

(assuming the larger size convention for the B-tiles), which can be summarized in a substitution matrix
Matrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...

equation:

Combining this with the decomposition of enlarged φA-tiles into B-tiles yields the substitution

so that the enlarged tile φA_L decomposes into two A_L tiles and one A_S tiles. The matching rules force a particular substitution: the two A_L tiles in a φA_L tile must form a kite – thus a kite decomposes into two kites and a two half-darts, and a dart decomposes into a kite and two half-darts. Enlarged φB-tiles decompose into B-tiles in a similar way (via φA-tiles).

Composition and decomposition can be iterated, so that, for example

The number of kites and darts in the nth iteration of the construction is determined by the nth power of the substitution matrix:

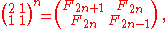
where F_n is the nth Fibonacci number

Fibonacci number

In mathematics, the Fibonacci numbers are the numbers in the following integer sequence:0,\;1,\;1,\;2,\;3,\;5,\;8,\;13,\;21,\;34,\;55,\;89,\;144,\; \ldots\; ....

. The ratio of numbers of kites to darts in any sufficiently large P2 Penrose tiling pattern therefore approximates to the golden ratio φ. A similar result holds for the ratio of the number of thick rhombs to thin rhombs in the P3 Penrose tiling.

Deflation for P2 and P3 tilings

Starting with a collection of tiles from a given tiling (which might be a single tile, a tiling of the plane, or any other collection), deflation proceeds with a sequence of steps called generations. In one generation of deflation, each tile is replaced with two or more new tiles that are scaled-down versions of tiles used in the original tiling. The substitution rules guarantee that the new tiles will be arranged in accordance with the matching rules. Repeated generations of deflation produce a tiling of the original axiom shape with smaller and smaller tiles.

Name	Initial tiles	Generation 1	Generation 2	Generation 3
Half-kite
Half-dart
Sun
Star

Consequences and applications

Inflation and deflation yield a method for constructing kite and dart (P2) tilings, or rhombus (P3) tilings, known as up-down generation.

The Penrose tilings, being non-periodic, have no translational symmetry – the pattern cannot be shifted to match itself over the entire plane. However, any bounded region, no matter how large, will be repeated an infinite number of times within the tiling. Therefore, a finite patch cannot differentiate between the uncountably many Penrose tilings, nor even determine which position within the tiling is being shown.

This shows in particular that the number of distinct Penrose tilings (of any type) is uncountably infinite. Up-down generation yields one method to parameterize the tilings, but other methods use Ammann bars, pentagrids, or cut and project schemes.

Decagonal coverings and quasicrystals

In 1996, German mathematician Petra Gummelt demonstrated that a covering (so called to distinguish it from a non-overlapping tiling) equivalent to the Penrose tiling can be constructed using a single decagonal tile if two kinds of overlapping regions are allowed. The decagonal tile is decorated with colored patches, and the covering rule allows only those overlaps compatible with the coloring. A suitable decomposition of the decagonal tile into kites and darts transforms such a covering into a Penrose (P2) tiling. Similarly, a P3 tiling can be obtained by inscribing a thick rhomb into each decagon; the remaining space is filled by thin rhombs.

These coverings have been considered as a realistic model for the growth of quasicrystals: the overlapping decagons are 'quasi-unit cells' analogous to the unit cells from which crystals are constructed, and the matching rules maximize the density of certain atomic clusters.

Related tilings

The three variants of the Penrose tiling are mutually locally derivable. Selecting some subsets from the vertices of a P1 tiling allows to produce other non-periodic tilings. If the corners of one pentagon in P1 are labeled in succession by 1,3,5,2,4 an unambiguous tagging in all the pentagons is established, the order being either clockwise or counterclockwise.
Points with the same label define a tiling by Robinson triangles while points with the numbers 3 and 4 on them define the vertices of a Tie-and-Navette tiling.

There are also other related unequivalent tilings, such as the hexagon-boat-star and Mikulla–Roth tilings. For instance, if the matching rules for the rhombus tiling are reduced to a specific restriction on the angles permitted at each vertex, a binary tiling is obtained. Its underlying symmetry is also fivefold but it is not a quasicrystal. It can be obtained either by decorating the rhombs of the original tiling with smaller ones, or by applying substitution rules, but not by de Bruijn's cut-and-project method.

Penrose tilings and art

The aesthetic value of tilings has long been appreciated, and remains a source of interest in them; here the visual appearance (rather than the formal defining properties) of Penrose tilings has attracted attention. The similarity with some decorative patterns

Girih tiles

Girih tiles are a set of five tiles that were used in the creation of tiling patterns for decoration of buildings in Islamic architecture...

used in the Middle East has been noted and Lu

Peter Lu

Peter James Lu, PhD is a post-doctoral research fellow in the Department of Physics and the School of Engineering and Applied Sciences at Harvard University in Cambridge, Massachusetts...

and Steinhardt

Paul Steinhardt

Paul J. Steinhardt is the Albert Einstein Professor of Science at Princeton University and a professor of theoretical physics. He received his B.S. at the California Institute of Technology and his Ph.D. in Physics at Harvard University...

have presented evidence that a Penrose tiling underlies some examples of medieval Islamic art.

Drop City

Drop City

Drop City was an artists' community that formed in southern Colorado in 1965. Abandoned by the early 1970s, it became known as the first rural "hippie commune".-Establishment:...

artist Clark Richert used Penrose rhombs in artwork in 1970. Art historian Martin Kemp

Martin Kemp (art historian)

Martin Kemp is Emeritus Research Professor in the History of Art at Oxford University. He has written and broadcast extensively on imagery in art and science from the Renaissance to the present day...

has observed that Albrecht Dürer