
Hexahedron
Encyclopedia
A hexahedron is any polyhedron
with six faces
, although usually implies the cube
as a regular
hexahedron with all its faces square
, and three squares around each vertex
.
There are seven topologically distinct convex hexahedra, one of which exists in two mirror image forms. (Two polyhedra are "topologically distinct" if they have intrinsically different arrangements of faces and vertices, such that it is impossible to distort one into the other simply by changing the lengths of edges or the angles between edges or faces.)
There are three further topologically distinct hexahedra that can only be realised as concave figures:
Polyhedron
In elementary geometry a polyhedron is a geometric solid in three dimensions with flat faces and straight edges...
with six faces
Face (geometry)
In geometry, a face of a polyhedron is any of the polygons that make up its boundaries. For example, any of the squares that bound a cube is a face of the cube...
, although usually implies the cube
Cube
In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and...
as a regular
Regular polyhedron
A regular polyhedron is a polyhedron whose faces are congruent regular polygons which are assembled in the same way around each vertex. A regular polyhedron is highly symmetrical, being all of edge-transitive, vertex-transitive and face-transitive - i.e. it is transitive on its flags...
hexahedron with all its faces square
Square (geometry)
In geometry, a square is a regular quadrilateral. This means that it has four equal sides and four equal angles...
, and three squares around each vertex
Vertex (geometry)
In geometry, a vertex is a special kind of point that describes the corners or intersections of geometric shapes.-Of an angle:...
.
There are seven topologically distinct convex hexahedra, one of which exists in two mirror image forms. (Two polyhedra are "topologically distinct" if they have intrinsically different arrangements of faces and vertices, such that it is impossible to distort one into the other simply by changing the lengths of edges or the angles between edges or faces.)
| Quadrilateral Quadrilateral In Euclidean plane geometry, a quadrilateral is a polygon with four sides and four vertices or corners. Sometimes, the term quadrangle is used, by analogy with triangle, and sometimes tetragon for consistency with pentagon , hexagon and so on... ly-faced hexahedra 46 faces, 12 edges, 8 vertices |
|||||
|---|---|---|---|---|---|
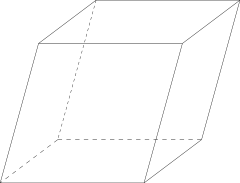 Parallelepiped Parallelepiped In geometry, a parallelepiped is a three-dimensional figure formed by six parallelograms. By analogy, it relates to a parallelogram just as a cube relates to a square. In Euclidean geometry, its definition encompasses all four concepts... (three pairs of parallelogram Parallelogram In Euclidean geometry, a parallelogram is a convex quadrilateral with two pairs of parallel sides. The opposite or facing sides of a parallelogram are of equal length and the opposite angles of a parallelogram are of equal measure... s) |
 Rhombohedron Rhombohedron In geometry, a rhombohedron is a three-dimensional figure like a cube, except that its faces are not squares but rhombi. It is a special case of a parallelepiped where all edges are the same length.... (three pairs of rhombi Rhombus In Euclidean geometry, a rhombus or rhomb is a convex quadrilateral whose four sides all have the same length. The rhombus is often called a diamond, after the diamonds suit in playing cards, or a lozenge, though the latter sometimes refers specifically to a rhombus with a 45° angle.Every... ) |
 Trigonal trapezohedron Trigonal trapezohedron In geometry, the trigonal trapezohedron or deltohedron is the first in an infinite series of face-uniform polyhedra which are dual to the antiprisms. It has six faces which are congruent rhombi.... (congruent rhombi Rhombus In Euclidean geometry, a rhombus or rhomb is a convex quadrilateral whose four sides all have the same length. The rhombus is often called a diamond, after the diamonds suit in playing cards, or a lozenge, though the latter sometimes refers specifically to a rhombus with a 45° angle.Every... ) |
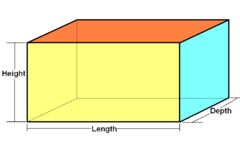 Cuboid Cuboid In geometry, a cuboid is a solid figure bounded by six faces, forming a convex polyhedron. There are two competing definitions of a cuboid in mathematical literature... (three pairs of rectangles) |
 Cube Cube In geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and... (square Square (geometry) In geometry, a square is a regular quadrilateral. This means that it has four equal sides and four equal angles... ) |
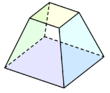 Quadrilateral frustum Frustum In geometry, a frustum is the portion of a solid that lies between two parallel planes cutting it.... (apex-truncated square pyramid Square pyramid In geometry, a square pyramid is a pyramid having a square base. If the apex is perpendicularly above the center of the square, it will have C4v symmetry.- Johnson solid :... ) |
| Others | |||||
Pentagonal pyramid Pentagonal pyramid In geometry, a pentagonal pyramid is a pyramid with a pentagonal base upon which are erected five triangular faces that meet at a point . Like any pyramid, it is self-dual.... (5.35) Faces 10 E, 6 V |
Triangular dipyramid Triangular dipyramid In geometry, the triangular bipyramid is the first in the infinite set of face-transitive bipyramids. It is the dual of the triangular prism with 6 isosceles triangle faces.... 36 Faces 9 E, 5 V |
5.4.4.3.3.3 Faces 11 E, 7 V |
5.5.4.4.3.3 Faces 12 E, 8 V |
4.4.4.4.3.3 Faces 11 E, 7 V |
Tetragonal antiwedge. Chiral – exists in "left-handed" and "right-handed" mirror image forms. 4.4.3.3.3.3 Faces 10 E, 6 V |
There are three further topologically distinct hexahedra that can only be realised as concave figures:
| 4.4.3.3.3.3 Faces 10 E, 6 V |
6.6.3.3.3.3 Faces 12 E, 8 V |
5.5.3.3.3.3 Faces 11 E, 7 V |
External links
- Polyhedra with 4-7 Faces by Steven Dutch
- CM2 HexaMesh Hex-dominant Delaunay mesh generator.

