Polyiamond
Encyclopedia
A polyiamond is a polyform
whose base form is an equilateral triangle. The word polyiamond is a back-formation
from diamond
, because this word is often used to describe the shape of a pair of equilateral triangles placed base to base, and the initial "di-" looked like a Greek
prefix meaning "two-".
is how many different polyiamonds exist with a given number of cells.
Like polyomino
es, polyiamonds may be free or one-sided.
Free polyiamonds are invariant under reflection as well as translation and rotation.
One-sided polyiamonds distinguish reflections.
The number of free n-iamonds for n = 1, 2, 3, … is :
The number of free polyiamonds with holes is given by ; the number of free polyiamonds without holes is given by ; the number of fixed polyiamonds is given by ; the number of one-sided polyiamonds is given by .
are mirror symmetry, 2-, 3-, and 6-fold rotational symmetry, and each combined with mirror symmetry.
2-fold rotational symmetry with and without mirror symmetry requires at least 2 and 4 triangles, respectively. 6-fold rotational symmetry with and without mirror symmetry requires at least 6 and 18 triangles, respectively. Asymmetry requires at least 5 triangles. 3-fold rotational symmetry without mirror symmetry requires at least 7 triangles.
In the case of only mirror symmetry we can distinguish having the symmetry axis aligned with the grid or rotated 30° (requires at least 4 and 3 triangles, respectively); ditto for 3-fold rotational symmetry, combined with mirror symmetry (requires at least 18 and 1 triangles, respectively).
es, but unlike polyhex
es, polyiamonds have three-dimension
al counterparts, formed by aggregating tetrahedra
. However, polytetrahedra
do not tile 3-space in the way polyiamonds can tile 2-space.
, as illustrated at right.
Conversely, every polyhex is also a polyiamond, because each hexagonal cell of a polyhex is the union of six adjacent equilateral triangles.
Polyform
In recreational mathematics, a polyform is a plane figure constructed by joining together identical basic polygons. The basic polygon is often a convex plane-filling polygon, such as a square or a triangle. More specific names have been given to polyforms resulting from specific basic polygons, as...
whose base form is an equilateral triangle. The word polyiamond is a back-formation
Back-formation
In etymology, back-formation is the process of creating a new lexeme, usually by removing actual or supposed affixes. The resulting neologism is called a back-formation, a term coined by James Murray in 1889...
from diamond
Diamond
In mineralogy, diamond is an allotrope of carbon, where the carbon atoms are arranged in a variation of the face-centered cubic crystal structure called a diamond lattice. Diamond is less stable than graphite, but the conversion rate from diamond to graphite is negligible at ambient conditions...
, because this word is often used to describe the shape of a pair of equilateral triangles placed base to base, and the initial "di-" looked like a Greek
Greek language
Greek is an independent branch of the Indo-European family of languages. Native to the southern Balkans, it has the longest documented history of any Indo-European language, spanning 34 centuries of written records. Its writing system has been the Greek alphabet for the majority of its history;...
prefix meaning "two-".
Counting polyiamonds
The basic combinatorial questionCombinatorics
Combinatorics is a branch of mathematics concerning the study of finite or countable discrete structures. Aspects of combinatorics include counting the structures of a given kind and size , deciding when certain criteria can be met, and constructing and analyzing objects meeting the criteria ,...
is how many different polyiamonds exist with a given number of cells.
Like polyomino
Polyomino
A polyomino is a plane geometric figure formed by joining one or more equal squares edge to edge. It is a polyform whose cells are squares. It may be regarded as a finite subset of the regular square tiling with a connected interior....
es, polyiamonds may be free or one-sided.
Free polyiamonds are invariant under reflection as well as translation and rotation.
One-sided polyiamonds distinguish reflections.
The number of free n-iamonds for n = 1, 2, 3, … is :
- 1, 1, 1, 3, 4, 12, 24, 66, 160, …
The number of free polyiamonds with holes is given by ; the number of free polyiamonds without holes is given by ; the number of fixed polyiamonds is given by ; the number of one-sided polyiamonds is given by .
| Name | Number of forms | Forms | ||||||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Moniamond | 1 | EWLINE
|
||||||||||||
| Diamond | 1 | EWLINE
|
||||||||||||
| Triamond | 1 | EWLINE
|
||||||||||||
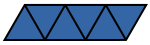
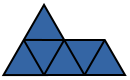
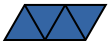
| Tetriamond | 3 | EWLINE
|
||||||||||||
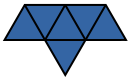
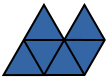
| Pentiamond | 4 | EWLINE
|
||||||||||||
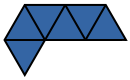
| Hexiamond | 12 | EWLINE
|
||||||||||||
Symmetries
Possible symmetriesSymmetry
Symmetry generally conveys two primary meanings. The first is an imprecise sense of harmonious or aesthetically pleasing proportionality and balance; such that it reflects beauty or perfection...
are mirror symmetry, 2-, 3-, and 6-fold rotational symmetry, and each combined with mirror symmetry.
2-fold rotational symmetry with and without mirror symmetry requires at least 2 and 4 triangles, respectively. 6-fold rotational symmetry with and without mirror symmetry requires at least 6 and 18 triangles, respectively. Asymmetry requires at least 5 triangles. 3-fold rotational symmetry without mirror symmetry requires at least 7 triangles.
In the case of only mirror symmetry we can distinguish having the symmetry axis aligned with the grid or rotated 30° (requires at least 4 and 3 triangles, respectively); ditto for 3-fold rotational symmetry, combined with mirror symmetry (requires at least 18 and 1 triangles, respectively).
 |
.svg.png) |
 |
 |
.svg.png) |
| Asymmetric | Mirror, 0° | Mirror, 30° | Rotational, 2-Fold | Mirror, 2-Fold |
 |
.svg.png) |
 |
 |
 |
| Rotational, 3-Fold | Mirror, 0°, 3-fold | Mirror, 30°, 3-fold | Rotational, 6-Fold | Mirror, 6-Fold |
Generalizations
Like polyominoPolyomino
A polyomino is a plane geometric figure formed by joining one or more equal squares edge to edge. It is a polyform whose cells are squares. It may be regarded as a finite subset of the regular square tiling with a connected interior....
es, but unlike polyhex
Polyhex (mathematics)
In recreational mathematics, a polyhex is a polyform with a regular hexagon as the base form.As with polyominoes, polyhexes may be enumerated as free polyhexes , fixed polyhexes and one-sided polyhexes In recreational mathematics, a polyhex is a polyform with a regular hexagon (or 'hex' for...
es, polyiamonds have three-dimension
Dimension
In physics and mathematics, the dimension of a space or object is informally defined as the minimum number of coordinates needed to specify any point within it. Thus a line has a dimension of one because only one coordinate is needed to specify a point on it...
al counterparts, formed by aggregating tetrahedra
Tetrahedron
In geometry, a tetrahedron is a polyhedron composed of four triangular faces, three of which meet at each vertex. A regular tetrahedron is one in which the four triangles are regular, or "equilateral", and is one of the Platonic solids...
. However, polytetrahedra
Polytetrahedron
Polytetrahedron is a term used for three distinct types of objects, all basedon the tetrahedron:*A uniform convex polychoron made up of 600 tetrahedral cells. It is more commonly known as a 600-cell or hexacosichoron...
do not tile 3-space in the way polyiamonds can tile 2-space.
Tessellations
Every polyiamond of order 6 or less tiles the plane. All but one of the heptiamonds tile the plane.Correspondence with Polyhexes
Every polyiamond corresponds to a polyhexPolyhex
Polyhex can mean:* Polyhex , a class of mathematical shapes* Polyhex , a fictional city in the Transformers stories...
, as illustrated at right.
Conversely, every polyhex is also a polyiamond, because each hexagonal cell of a polyhex is the union of six adjacent equilateral triangles.
External links
- VERHEXT — a 1960s puzzle game by Heinz HaberHeinz HaberHeinz Haber was a German physicist and science writer who primarily became famous for his TV programs and books about physics and environmental subjects...
based on hexiamonds