
Honeycomb (geometry)
Encyclopedia

Geometry
Geometry arose as the field of knowledge dealing with spatial relationships. Geometry was one of the two fields of pre-modern mathematics, the other being the study of numbers ....
, a honeycomb is a space filling or close packing of polyhedral or higher-dimensional cells, so that there are no gaps. It is an example of the more general mathematical tiling or tessellation
Tessellation
A tessellation or tiling of the plane is a pattern of plane figures that fills the plane with no overlaps and no gaps. One may also speak of tessellations of parts of the plane or of other surfaces. Generalizations to higher dimensions are also possible. Tessellations frequently appeared in the art...
in any number of dimensions.
Honeycombs are usually constructed in ordinary Euclidean
Euclidean geometry
Euclidean geometry is a mathematical system attributed to the Alexandrian Greek mathematician Euclid, which he described in his textbook on geometry: the Elements. Euclid's method consists in assuming a small set of intuitively appealing axioms, and deducing many other propositions from these...
("flat") space. They may also be constructed in non-Euclidean spaces
Non-Euclidean geometry
Non-Euclidean geometry is the term used to refer to two specific geometries which are, loosely speaking, obtained by negating the Euclidean parallel postulate, namely hyperbolic and elliptic geometry. This is one term which, for historical reasons, has a meaning in mathematics which is much...
, such as hyperbolic honeycombs. Any finite uniform polytope
Polytope
In elementary geometry, a polytope is a geometric object with flat sides, which exists in any general number of dimensions. A polygon is a polytope in two dimensions, a polyhedron in three dimensions, and so on in higher dimensions...
can be projected to its circumsphere to form a uniform honeycomb in spherical space.

Classification
There are infinitely many honeycombs, which have only been partially classified. The more regular ones have attracted the most interest, while a rich and varied assortment of others continue to be discovered.The simplest honeycombs to build are formed from stacked layers or slabs of prisms
Prism (geometry)
In geometry, a prism is a polyhedron with an n-sided polygonal base, a translated copy , and n other faces joining corresponding sides of the two bases. All cross-sections parallel to the base faces are the same. Prisms are named for their base, so a prism with a pentagonal base is called a...
based on some tessellation of the plane. In particular, for every parallelepiped
Parallelepiped
In geometry, a parallelepiped is a three-dimensional figure formed by six parallelograms. By analogy, it relates to a parallelogram just as a cube relates to a square. In Euclidean geometry, its definition encompasses all four concepts...
, copies can fill space, with the cubic honeycomb
Cubic honeycomb
The cubic honeycomb is the only regular space-filling tessellation in Euclidean 3-space, made up of cubic cells. It has 4 cubes around every edge, and 8 cubes around each vertex. Its vertex figure is a regular octahedron....
being special because it is the only regular honeycomb in ordinary (Euclidean) space. Another interesting family is the Hill tetrahedra
Hill tetrahedron
In geometry, the Hill tetrahedra are a family of space-filling tetrahedra. They were discovered in 1896 by M.J.M. Hill, a professor of mathematics at the University College London, who showed that they are scissor-congruent to a cube.- Construction :...
and their generalizations, which can also tile the space.
Uniform honeycombs
A uniform honeycomb is a honeycomb in Euclidean 3-space composed of uniform polyhedralUniform polyhedron
A uniform polyhedron is a polyhedron which has regular polygons as faces and is vertex-transitive...
cells
Cell (geometry)
In geometry, a cell is a three-dimensional element that is part of a higher-dimensional object.- In polytopes :A cell is a three-dimensional polyhedron element that is part of the boundary of a higher-dimensional polytope, such as a polychoron or honeycomb For example, a cubic honeycomb is made...
, and having all vertices the same (i.e., the group of [isometries of 3-space that preserve the tiling] is transitive on vertices
Vertex-transitive
In geometry, a polytope is isogonal or vertex-transitive if, loosely speaking, all its vertices are the same...
). There are 28 convex
Convex polytope
A convex polytope is a special case of a polytope, having the additional property that it is also a convex set of points in the n-dimensional space Rn...
examples, also called the Archimedean honeycombs
Convex uniform honeycomb
In geometry, a convex uniform honeycomb is a uniform tessellation which fills three-dimensional Euclidean space with non-overlapping convex uniform polyhedral cells.Twenty-eight such honeycombs exist:* the familiar cubic honeycomb and 7 truncations thereof;...
. Of these, just one is regular and one quasiregular:
- Regular honeycomb: CubeCubeIn geometry, a cube is a three-dimensional solid object bounded by six square faces, facets or sides, with three meeting at each vertex. The cube can also be called a regular hexahedron and is one of the five Platonic solids. It is a special kind of square prism, of rectangular parallelepiped and...
s. - Quasiregular honeycomb: Octahedra and tetrahedra.
Space-filling polyhedra
A honeycomb having all cells identical within its symmetries is said to be cell-transitive or isochoric. A cell of such a honeycomb is said to be a space-filling polyhedron. Known examples include:- The regular packings of cubesCubic honeycombThe cubic honeycomb is the only regular space-filling tessellation in Euclidean 3-space, made up of cubic cells. It has 4 cubes around every edge, and 8 cubes around each vertex. Its vertex figure is a regular octahedron....
, hexagonal prismsHexagonal prismatic honeycombThe hexagonal prismatic honeycomb is a space-filling tessellation in Euclidean 3-space made up of hexagonal prisms.It is constructed from a hexagonal tiling extruded into prisms.It is one of 28 convex uniform honeycombs.- References :...
, and triangular prismsTriangular prismatic honeycombThe triangular prismatic honeycomb is a space-filling tessellation in Euclidean 3-space. It is composed entirely of triangular prisms.It is constructed from a triangular tiling extruded into prisms.It is one of 28 convex uniform honeycombs....
. - The uniform packing of truncated octahedraBitruncated cubic honeycombThe bitruncated cubic honeycomb is a space-filling tessellation in Euclidean 3-space made up of truncated octahedra.It is one of 28 uniform honeycombs. It has 4 truncated octahedra around each vertex....
. - The rhombic dodecahedral honeycombRhombic dodecahedral honeycombThe rhombic dodecahedra honeycomb is a space-filling tessellation in Euclidean 3-space. It is the Voronoi diagram of the face-centered cubic sphere-packing, which is believed to be the densest possible packing of equal spheres in ordinary space .It consists of copies of a single cell, the rhombic...
. - The trapezo-rhombic dodecahedral honeycombTrapezo-rhombic dodecahedral honeycombThe trapezo-rhombic dodecahedral honeycomb is a space-filling tessellation in Euclidean 3-space.It consists of copies of a single cell, the trapezo-rhombic dodecahedron....
. - The rhombo-hexagonal dodecahedronRhombo-hexagonal dodecahedronThe rhombo-hexagonal dodecahedron is a convex polyhedron with 8 rhombic and 4 equilateral hexagonal faces.It is also called an elongated dodecahedron and extended rhombic dodecahedron because it is related to the rhombic dodecahedron by expanding four rhombic faces of the rhombic dodecahedron into...
honeycomb. - A packing of any cuboidCuboidIn geometry, a cuboid is a solid figure bounded by six faces, forming a convex polyhedron. There are two competing definitions of a cuboid in mathematical literature...
, rhombic hexahedronHexahedronA hexahedron is any polyhedron with six faces, although usually implies the cube as a regular hexahedron with all its faces square, and three squares around each vertex....
or parallelepipedParallelepipedIn geometry, a parallelepiped is a three-dimensional figure formed by six parallelograms. By analogy, it relates to a parallelogram just as a cube relates to a square. In Euclidean geometry, its definition encompasses all four concepts...
. - Isohedral simple tilings.
 |
 |
Sometimes, two or more different polyhedra may be combined to fill space. Besides many of the uniform honeycombs, another well known example is the Weaire–Phelan structure, adopted from the structure of clathrate hydrate crystals
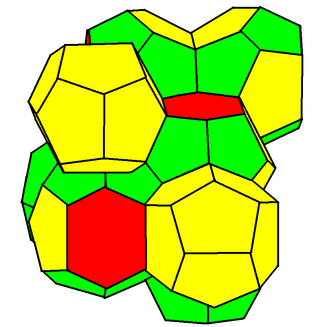
Non-convex honeycombs
Documented examples are rare. Two classes can be distinguished:- Non-convex cells which pack without overlapping, analogous to tilings of concave polygons. These include a packing of the small stellated rhombic dodecahedron.
- Overlapping of cells whose positive and negative densities 'cancel out' to form a uniformly dense continuum, analogous to overlapping tilings of the plane.

Hyperbolic honeycombs
In hyperbolic spaceHyperbolic space
In mathematics, hyperbolic space is a type of non-Euclidean geometry. Whereas spherical geometry has a constant positive curvature, hyperbolic geometry has a negative curvature: every point in hyperbolic space is a saddle point...
, the dihedral angle
Dihedral angle
In geometry, a dihedral or torsion angle is the angle between two planes.The dihedral angle of two planes can be seen by looking at the planes "edge on", i.e., along their line of intersection...
of a polyhedron depends on its size. The regular hyperbolic honeycombs thus include two with four or five dodecahedra meeting at each edge; their dihedral angles thus are π/2 and 2π/5, both of which are less than that of a Euclidean dodecahedron. Apart from this effect, the hyperbolic honeycombs obey the same topological constraints as Euclidean honeycombs and polychora.
The 4 regular hyperbolic honeycombs and many uniform hyperbolic honeycombs
Convex uniform honeycombs in hyperbolic space
In geometry, a convex uniform honeycomb is a tessellation of convex uniform polyhedron cells. In 3-dimensional hyperbolic space there are nine Coxeter group families of compact convex uniform honeycombs, generated as Wythoff constructions, and represented by ring permutations of the Coxeter–Dynkin...
have been enumerated.
Duality of honeycombs
For every honeycomb there is a dual honeycomb, which may be obtained by exchanging:- cells for vertices.
- walls for edges.
These are just the rules for dualising four-dimensional polychora
Polychoron
In geometry, a polychoron or 4-polytope is a four-dimensional polytope. It is a connected and closed figure, composed of lower dimensional polytopal elements: vertices, edges, faces , and cells...
, except that the usual finite method of reciprocation about a concentric hypersphere can run into problems.
The more regular honeycombs dualise neatly:
- The cubic honeycomb is self-dual.
- That of octahedra and tetrahedra is dual to that of rhombic dodecahedra.
- The slab honeycombs derived from uniform plane tilings are dual to each other in the same way that the tilings are.
- The duals of the remaining Archimedean honeycombs are all cell-transitive and have been described by Inchbald.
Self-dual honeycombs
Honeycombs can also be self-dual. All n-dimensional hypercubic honeycombs with Schlafli symbols {4,3n−2,4}, are self-dual.See also
- List of uniform tilings
- Regular honeycombs
External links
- Five space-filling polyhedra, Guy Inchbald
- The Archimedean honeycomb duals, Guy Inchbald, The Mathematical Gazette 80, November 1996, p.p. 466-475.

