
Hyperbolic growth
Encyclopedia
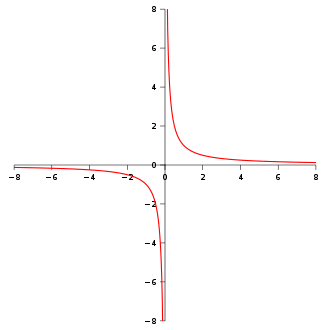
Mathematical singularity
In mathematics, a singularity is in general a point at which a given mathematical object is not defined, or a point of an exceptional set where it fails to be well-behaved in some particular way, such as differentiability...
under a finite variation (a "finite-time singularity") it is said to undergo hyperbolic growth.
More precisely, the reciprocal function
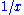 has a hyperbola
has a hyperbolaHyperbola
In mathematics a hyperbola is a curve, specifically a smooth curve that lies in a plane, which can be defined either by its geometric properties or by the kinds of equations for which it is the solution set. A hyperbola has two pieces, called connected components or branches, which are mirror...
as a graph, and has a singularity at 0, meaning that the limit
Limit of a function
In mathematics, the limit of a function is a fundamental concept in calculus and analysis concerning the behavior of that function near a particular input....
as
 is infinity: any similar graph is said to exhibit hyperbolic growth.
is infinity: any similar graph is said to exhibit hyperbolic growth.Description
If the output of a function is inversely proportional to its input, or inversely proportional to the difference from a given value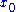 , the function will exhibit hyperbolic growth, with a singularity at
, the function will exhibit hyperbolic growth, with a singularity at 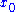 .
.In the real world hyperbolic growth is created by certain non-linear positive feedback
Positive feedback
Positive feedback is a process in which the effects of a small disturbance on a system include an increase in the magnitude of the perturbation. That is, A produces more of B which in turn produces more of A. In contrast, a system that responds to a perturbation in a way that reduces its effect is...
mechanisms.
Comparisons with other growth
Like exponential growthExponential growth
Exponential growth occurs when the growth rate of a mathematical function is proportional to the function's current value...
and logistic growth, hyperbolic growth is highly nonlinear, but differs in important respects.
These functions can be confused, as exponential growth, hyperbolic growth, and the first half of logistic growth are convex function
Convex function
In mathematics, a real-valued function f defined on an interval is called convex if the graph of the function lies below the line segment joining any two points of the graph. Equivalently, a function is convex if its epigraph is a convex set...
s; however their asymptotic behavior (behavior as input gets large) differs dramatically:
- logistic growth is constrained (has a finite limit, even as time goes to infinity),
- exponential growth grows to infinity as time goes to infinity (but is always finite for finite time),
- hyperbolic growth has a singularity in finite time (grows to infinity at a finite time).
Population
Certain mathematical models suggest that until the early 1970s the world populationWorld population
The world population is the total number of living humans on the planet Earth. As of today, it is estimated to be billion by the United States Census Bureau...
underwent hyperbolic growth (see, e.g., Introduction to Social Macrodynamics by Andrey Korotayev
Andrey Korotayev
Andrey Korotayev is an anthropologist, economic historian, and sociologist, with major contributions to world-systems theory, cross-cultural studies, Near Eastern history, and mathematical modeling of social and economic macrodynamics.Education and career=Born in Moscow, Andrey Korotayev attended...
et al.). It was also shown that till the 1970s the hyperbolic growth of the world population was accompanied by quadratic-hyperbolic growth of the world GDP, and developed a number of mathematical model
Mathematical model
A mathematical model is a description of a system using mathematical concepts and language. The process of developing a mathematical model is termed mathematical modeling. Mathematical models are used not only in the natural sciences and engineering disciplines A mathematical model is a...
s describing both this phenomenon, and the World System withdrawal from the blow-up regime observed in the recent decades. The hyperbolic growth of the world population
World population
The world population is the total number of living humans on the planet Earth. As of today, it is estimated to be billion by the United States Census Bureau...
and quadratic-hyperbolic growth of the world GDP observed till the 1970s have been correlated by Andrey Korotayev
Andrey Korotayev
Andrey Korotayev is an anthropologist, economic historian, and sociologist, with major contributions to world-systems theory, cross-cultural studies, Near Eastern history, and mathematical modeling of social and economic macrodynamics.Education and career=Born in Moscow, Andrey Korotayev attended...
and his colleagues to a non-linear second order positive feedback
Positive feedback
Positive feedback is a process in which the effects of a small disturbance on a system include an increase in the magnitude of the perturbation. That is, A produces more of B which in turn produces more of A. In contrast, a system that responds to a perturbation in a way that reduces its effect is...
between the demographic growth and technological development, described by a chain of causation: technological growth leads to more carrying capacity
Carrying capacity
The carrying capacity of a biological species in an environment is the maximum population size of the species that the environment can sustain indefinitely, given the food, habitat, water and other necessities available in the environment...
of land for people, which leads to more people, which leads to more inventors, which in turn leads to yet more technological growth, and on and on. Other models suggest exponential growth, logistic growth, or other functions.
Queuing theory
Another example of hyperbolic growth can be found in queuing theory: the average waiting time of randomly arriving customers grows hyperbolically as a function of the average load ratio of the server. The singularity in this case occurs when the average amount of work arriving to the server equals the server's processing capacity. If the processing needs exceed the server's capacity, then there is no well-defined average waiting time, as the queue can grow without bound. A practical implication of this particular example is that for highly loaded queuing systems the average waiting time can be extremely sensitive to the processing capacity.Enzyme kinetics
A further practical example of hyperbolic growth can be found in enzyme kineticsEnzyme kinetics
Enzyme kinetics is the study of the chemical reactions that are catalysed by enzymes. In enzyme kinetics, the reaction rate is measured and the effects of varying the conditions of the reaction investigated...
. When the rate of reaction (termed velocity) between an enzyme
Enzyme
Enzymes are proteins that catalyze chemical reactions. In enzymatic reactions, the molecules at the beginning of the process, called substrates, are converted into different molecules, called products. Almost all chemical reactions in a biological cell need enzymes in order to occur at rates...
and substrate
Substrate (biochemistry)
In biochemistry, a substrate is a molecule upon which an enzyme acts. Enzymes catalyze chemical reactions involving the substrate. In the case of a single substrate, the substrate binds with the enzyme active site, and an enzyme-substrate complex is formed. The substrate is transformed into one or...
is plotted against various concentrations of the substrate, a hyperbolic plot is obtained for many simpler systems. When this happens, the enzyme is said to follow Michaelis-Menten kinetics.
Mathematical example
The function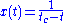
exhibits hyperbolic growth with a singularity at time
 : in the limit
: in the limitLimit of a function
In mathematics, the limit of a function is a fundamental concept in calculus and analysis concerning the behavior of that function near a particular input....
as
 , the function goes to infinity.
, the function goes to infinity.More generally, the function
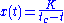
exhibits hyperbolic growth, where
 is a scale factor
is a scale factorScale factor
A scale factor is a number which scales, or multiplies, some quantity. In the equation y=Cx, C is the scale factor for x. C is also the coefficient of x, and may be called the constant of proportionality of y to x...
.
Note that this algebraic function can be regarded as analytical solution for the function's differential:
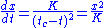
This means that with hyperbolic growth the absolute growth rate of the variable x in the moment t is proportional to the square of the value of x in the moment t.
Respectively, the quadratic-hyperbolic function looks as follows:
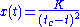 .
.See also
- Heinz von FoersterHeinz von FoersterHeinz von Foerster was an Austrian American scientist combining physics and philosophy. Together with Warren McCulloch, Norbert Wiener, John von Neumann, Lawrence J. Fogel, and others, Heinz von Foerster was an architect of cybernetics.-Biography:Von Foerster was born in 1911 in Vienna, Austria,...
- Technological singularityTechnological singularityTechnological singularity refers to the hypothetical future emergence of greater-than-human intelligence through technological means. Since the capabilities of such an intelligence would be difficult for an unaided human mind to comprehend, the occurrence of a technological singularity is seen as...
- Paradigm shiftParadigm shiftA Paradigm shift is, according to Thomas Kuhn in his influential book The Structure of Scientific Revolutions , a change in the basic assumptions, or paradigms, within the ruling theory of science...
- List of paradigm shifts in science
- Scientific mythology
- Social effect of evolutionary theorySocial effect of evolutionary theoryThe social effects of evolutionary thought have been considerable. As the scientific explanation of life's diversity has developed, it has often displaced alternative, sometimes very widely held, explanations. Because the theory of evolution includes an explanation of humanity's origins, it has...
- Deep ecologyDeep ecologyDeep ecology is a contemporary ecological philosophy that recognizes an inherent worth of all living beings, regardless of their instrumental utility to human needs. The philosophy emphasizes the interdependence of organisms within ecosystems and that of ecosystems with each other within the...

