
Inverse-square law
Encyclopedia
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
, an inverse-square law is any physical law
Physical law
A physical law or scientific law is "a theoretical principle deduced from particular facts, applicable to a defined group or class of phenomena, and expressible by the statement that a particular phenomenon always occurs if certain conditions be present." Physical laws are typically conclusions...
stating that a specified physical quantity
Quantity
Quantity is a property that can exist as a magnitude or multitude. Quantities can be compared in terms of "more" or "less" or "equal", or by assigning a numerical value in terms of a unit of measurement. Quantity is among the basic classes of things along with quality, substance, change, and relation...
or strength is inversely proportional to the square of the distance
Distance
Distance is a numerical description of how far apart objects are. In physics or everyday discussion, distance may refer to a physical length, or an estimation based on other criteria . In mathematics, a distance function or metric is a generalization of the concept of physical distance...
from the source of that physical quantity.
The divergence of a vector field
Vector field
In vector calculus, a vector field is an assignmentof a vector to each point in a subset of Euclidean space. A vector field in the plane for instance can be visualized as an arrow, with a given magnitude and direction, attached to each point in the plane...
which is the resultant of radial inverse-square law fields with respect to one or more sources is everywhere proportional to the strength of the local sources, and hence zero outside sources.
Justification
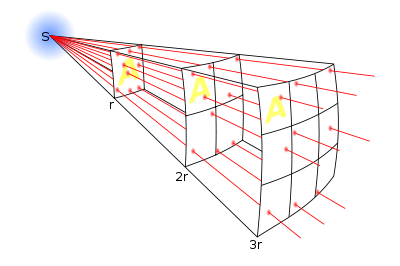
The inverse-square law generally applies when some force, energy, or other conserved quantity is radiated outward radially in three-dimensional spaceThree-dimensional space
Three-dimensional space is a geometric 3-parameters model of the physical universe in which we live. These three dimensions are commonly called length, width, and depth , although any three directions can be chosen, provided that they do not lie in the same plane.In physics and mathematics, a...
from a point source
Point source
A point source is a localised, relatively small source of something.Point source may also refer to:*Point source , a localised source of pollution**Point source water pollution, water pollution with a localized source...
. Since the surface area
Surface area
Surface area is the measure of how much exposed area a solid object has, expressed in square units. Mathematical description of the surface area is considerably more involved than the definition of arc length of a curve. For polyhedra the surface area is the sum of the areas of its faces...
of a sphere
Sphere
A sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...
(which is 4πr2 ) is proportional to the square of the radius, as the emitted radiation gets farther from the source, it is spread out over an area that is increasing in proportion to the square of the distance from the source. Hence, the intensity of radiation passing through any unit area (directly facing the point source) is inversely proportional to the square of the distance from the point source. Gauss's law
Gauss's law
In physics, Gauss's law, also known as Gauss's flux theorem, is a law relating the distribution of electric charge to the resulting electric field. Gauss's law states that:...
applies to and can be used with any physical quantity that acts in accord to the inverse-square relationship.
Gravitation
Gravitation is the attraction of two objects with mass. This law states:- The gravitational attraction force between two point masses is directly proportional to the product of their masses and inversely proportional to the square of their separation distance. The force is always attractive and acts along the line joining them from their center.
If the distribution of matter in each body is spherically symmetric, then the objects can be treated as point masses without approximation, as shown in the shell theorem
Shell theorem
In classical mechanics, the shell theorem gives gravitational simplifications that can be applied to objects inside or outside a spherically symmetrical body...
. Otherwise, if we want to calculate the attraction between massive bodies, we need to add all the point-point attraction forces vectorially and the net attraction might not be exact inverse square. However, if the separation between the massive bodies is much larger compared to their sizes, then to a good approximation, it is reasonable to treat the masses as point mass while calculating the gravitational force.
As the law of gravitation, this law was suggested in 1645 by Ismael Bullialdus
Ismaël Bullialdus
Ismaël Bullialdus was a French astronomer.Bullialdus was born Ismaël Boulliau in Loudun, Vienne, France, the first surviving son to Calvinists Susanna Motet and Ismaël Boulliau, a notary by profession and amateur astronomer. At age twenty-one he converted to Catholicism, and by twenty-six was...
. But Bullialdus did not accept Kepler’s second and third laws
Kepler's laws of planetary motion
In astronomy, Kepler's laws give a description of the motion of planets around the Sun.Kepler's laws are:#The orbit of every planet is an ellipse with the Sun at one of the two foci....
, nor did he appreciate Christiaan Huygens’s solution for circular motion (motion in a straight line pulled aside by the central force). Indeed, Bullialdus maintained the sun’s force was attractive at aphelion and repulsive at perihelion. Robert Hooke
Robert Hooke
Robert Hooke FRS was an English natural philosopher, architect and polymath.His adult life comprised three distinct periods: as a scientific inquirer lacking money; achieving great wealth and standing through his reputation for hard work and scrupulous honesty following the great fire of 1666, but...
and Giovanni Alfonso Borelli
Giovanni Alfonso Borelli
Giovanni Alfonso Borelli was a Renaissance Italian physiologist, physicist, and mathematician. He contributed to the modern principle of scientific investigation by continuing Galileo's custom of testing hypotheses against observation...
both expounded gravitation in 1666 as an attractive force (Hooke’s lecture “On gravity” at the Royal Society, London, on 21 March; Borelli’s "Theory of the Planets", published later in 1666). Hooke’s 1670 Gresham lecture explained that gravitation applied to “all celestiall bodys” and added the principles that the gravitating power decreases with distance and that in the absence of any such power bodies move in straight lines. By 1679, Hooke thought gravitation had inverse square dependence and communicated this in a letter to Isaac Newton
Isaac Newton
Sir Isaac Newton PRS was an English physicist, mathematician, astronomer, natural philosopher, alchemist, and theologian, who has been "considered by many to be the greatest and most influential scientist who ever lived."...
. Hooke remained bitter about Newton claiming the invention of this principle, even though Newton’s “Principia” acknowledged that Hooke, along with Wren and Halley, had separately appreciated the inverse square law in the solar system, as well as giving some credit to Bullialdus.
Electrostatics
The force of attraction or repulsion between two electrically charged particles, in addition to being directly proportional to the product of the electric charges, is inversely proportional to the square of the distance between them; this is known as Coulomb's lawCoulomb's law
Coulomb's law or Coulomb's inverse-square law, is a law of physics describing the electrostatic interaction between electrically charged particles. It was first published in 1785 by French physicist Charles Augustin de Coulomb and was essential to the development of the theory of electromagnetism...
. The deviation of the exponent from 2 is less than one part in 1015.
Light and other electromagnetic radiation
The intensityIntensity (physics)
In physics, intensity is a measure of the energy flux, averaged over the period of the wave. The word "intensity" here is not synonymous with "strength", "amplitude", or "level", as it sometimes is in colloquial speech...
(or illuminance
Illuminance
In photometry, illuminance is the total luminous flux incident on a surface, per unit area. It is a measure of the intensity of the incident light, wavelength-weighted by the luminosity function to correlate with human brightness perception. Similarly, luminous emittance is the luminous flux per...
or irradiance
Irradiance
Irradiance is the power of electromagnetic radiation per unit area incident on a surface. Radiant emittance or radiant exitance is the power per unit area radiated by a surface. The SI units for all of these quantities are watts per square meter , while the cgs units are ergs per square centimeter...
) of light
Light
Light or visible light is electromagnetic radiation that is visible to the human eye, and is responsible for the sense of sight. Visible light has wavelength in a range from about 380 nanometres to about 740 nm, with a frequency range of about 405 THz to 790 THz...
or other linear waves radiating from a point source
Point source
A point source is a localised, relatively small source of something.Point source may also refer to:*Point source , a localised source of pollution**Point source water pollution, water pollution with a localized source...
(energy per unit of area perpendicular to the source) is inversely proportional to the square of the distance from the source; so an object (of the same size) twice as far away, receives only one-quarter the energy
Energy
In physics, energy is an indirectly observed quantity. It is often understood as the ability a physical system has to do work on other physical systems...
(in the same time period).
More generally, the irradiance, i.e., the intensity (or power
Power (physics)
In physics, power is the rate at which energy is transferred, used, or transformed. For example, the rate at which a light bulb transforms electrical energy into heat and light is measured in watts—the more wattage, the more power, or equivalently the more electrical energy is used per unit...
per unit area in the direction of propagation
Wave propagation
Wave propagation is any of the ways in which waves travel.With respect to the direction of the oscillation relative to the propagation direction, we can distinguish between longitudinal wave and transverse waves....
), of a spherical
Sphere
A sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...
wavefront
Wavefront
In physics, a wavefront is the locus of points having the same phase. Since infrared, optical, x-ray and gamma-ray frequencies are so high, the temporal component of electromagnetic waves is usually ignored at these wavelengths, and it is only the phase of the spatial oscillation that is described...
varies inversely with the square of the distance from the source (assuming there are no losses caused by absorption or scattering
Scattering
Scattering is a general physical process where some forms of radiation, such as light, sound, or moving particles, are forced to deviate from a straight trajectory by one or more localized non-uniformities in the medium through which they pass. In conventional use, this also includes deviation of...
).
For example, the intensity of radiation from the Sun
Sun
The Sun is the star at the center of the Solar System. It is almost perfectly spherical and consists of hot plasma interwoven with magnetic fields...
is 9126 watt
Watt
The watt is a derived unit of power in the International System of Units , named after the Scottish engineer James Watt . The unit, defined as one joule per second, measures the rate of energy conversion.-Definition:...
s per square meter at the distance of Mercury
Mercury (planet)
Mercury is the innermost and smallest planet in the Solar System, orbiting the Sun once every 87.969 Earth days. The orbit of Mercury has the highest eccentricity of all the Solar System planets, and it has the smallest axial tilt. It completes three rotations about its axis for every two orbits...
(0.387 AU
Astronomical unit
An astronomical unit is a unit of length equal to about or approximately the mean Earth–Sun distance....
); but only 1367 watts per square meter at the distance of Earth
Earth
Earth is the third planet from the Sun, and the densest and fifth-largest of the eight planets in the Solar System. It is also the largest of the Solar System's four terrestrial planets...
(1 AU)—an approximate threefold increase in distance results in an approximate ninefold decrease in intensity of radiation.
In photography
Photography
Photography is the art, science and practice of creating durable images by recording light or other electromagnetic radiation, either electronically by means of an image sensor or chemically by means of a light-sensitive material such as photographic film...
and theatrical lighting, the inverse-square law is used to determine the "fall off" or the difference in illumination on a subject as it moves closer to or further from the light source. For quick approximations, it is enough to remember that doubling the distance reduces illumination to one quarter; or similarly, to halve the illumination increase the distance by a factor of 1.4 (the square root of 2), and to double illumination, reduce the distance to 0.7 (square root of 1/2). When the illuminant is not a point source, the inverse square rule is often still a useful approximation; when the size of the light source is less than one-fifth of the distance to the subject, the calculation error is less than 1%.
The fractional reduction in electromagnetic fluence
Fluence
In physics, fluence is the flux integrated over time. For particles, it is defined as the total number of particles that intersect a unit area in a specific time interval of interest, and has units of m–2...
(Φ) for indirectly ionizing radiation with increasing distance from a point source can be calculated using the inverse-square law. Since emissions from a point source have radial directions, they intercept at a perpendicular incidence. The area of such a shell is
 where r is the radial distance from the center. The law is particularly important in diagnostic radiography
where r is the radial distance from the center. The law is particularly important in diagnostic radiographyRadiography
Radiography is the use of X-rays to view a non-uniformly composed material such as the human body. By using the physical properties of the ray an image can be developed which displays areas of different density and composition....
and radiotherapy treatment planning, though this proportionality does not hold in practical situations unless source dimensions are much smaller than the distance.
Example
Let the total power radiated from a point source, for example, an omnidirectional isotropic antenna, be P. At large distances from the source (compared to the size of the source), this power is distributed over larger and larger spherical surfaces as the distance from the source increases. Since the surface area of a sphere of radius r is A = 4πr 2, then intensityIntensity (physics)
In physics, intensity is a measure of the energy flux, averaged over the period of the wave. The word "intensity" here is not synonymous with "strength", "amplitude", or "level", as it sometimes is in colloquial speech...
I (power per unit area) of radiation at distance r is

The energy or intensity decreases (divided by 4) as the distance r is doubled; measured in dB
Decibel
The decibel is a logarithmic unit that indicates the ratio of a physical quantity relative to a specified or implied reference level. A ratio in decibels is ten times the logarithm to base 10 of the ratio of two power quantities...
it would decrease by 6.02 dB per doubling of distance.
Acoustics
In acousticsAcoustics
Acoustics is the interdisciplinary science that deals with the study of all mechanical waves in gases, liquids, and solids including vibration, sound, ultrasound and infrasound. A scientist who works in the field of acoustics is an acoustician while someone working in the field of acoustics...
one usually measures the sound pressure
Sound pressure
Sound pressure or acoustic pressure is the local pressure deviation from the ambient atmospheric pressure caused by a sound wave. Sound pressure can be measured using a microphone in air and a hydrophone in water...
at a given distance r from the source using the 1/r law. Since intensity is proportional to the square of pressure amplitude, this is just a variation on the inverse-square law.
Example
In acousticsAcoustics
Acoustics is the interdisciplinary science that deals with the study of all mechanical waves in gases, liquids, and solids including vibration, sound, ultrasound and infrasound. A scientist who works in the field of acoustics is an acoustician while someone working in the field of acoustics...
, the sound pressure
Sound pressure
Sound pressure or acoustic pressure is the local pressure deviation from the ambient atmospheric pressure caused by a sound wave. Sound pressure can be measured using a microphone in air and a hydrophone in water...
of a spherical
Sphere
A sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...
wavefront
Wavefront
In physics, a wavefront is the locus of points having the same phase. Since infrared, optical, x-ray and gamma-ray frequencies are so high, the temporal component of electromagnetic waves is usually ignored at these wavelengths, and it is only the phase of the spatial oscillation that is described...
radiating from a point source decreases by 50% as the distance r is doubled; measured in dB
Decibel
The decibel is a logarithmic unit that indicates the ratio of a physical quantity relative to a specified or implied reference level. A ratio in decibels is ten times the logarithm to base 10 of the ratio of two power quantities...
, the decreases is still 6.02 dB, since dB represents an intensity ratio. The behaviour is not inverse-square, but is inverse-proportional (inverse distance law):

The same is true for the component of particle velocity
Particle velocity
Particle velocity is the velocity v of a particle in a medium as it transmits a wave. In many cases this is a longitudinal wave of pressure as with sound, but it can also be a transverse wave as with the vibration of a taut string....
 that is in-phase with the instantaneous sound pressure
that is in-phase with the instantaneous sound pressure 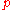 :
: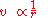
In the near field
Near and far field
The near field and far field and the transition zone are regions of the electromagnetic radiation field that emanates from a transmitting antenna, or as a result of radiation scattering off an object...
is a quadrature component of the particle velocity that is 90° out of phase with the sound pressure and does not contribute to the time-averaged energy or the intensity of the sound. The sound intensity
Sound intensity
Sound intensity or acoustic intensity is defined as the sound power Pac per unit area A. The usual context is the noise measurement of sound intensity in the air at a listener's location.-Acoustic intensity:...
is the product of the RMS
Root mean square
In mathematics, the root mean square , also known as the quadratic mean, is a statistical measure of the magnitude of a varying quantity. It is especially useful when variates are positive and negative, e.g., sinusoids...
sound pressure and the in-phase component of the RMS particle velocity, both of which are inverse-proportional. Accordingly, the intensity follows an inverse-square behaviour:

Field theory interpretation
For an irrotational vector fieldIrrotational vector field
In vector calculus a conservative vector field is a vector field which is the gradient of a function, known in this context as a scalar potential. Conservative vector fields have the property that the line integral from one point to another is independent of the choice of path connecting the two...
in three-dimensional space the inverse-square law corresponds to the property that the divergence
Divergence
In vector calculus, divergence is a vector operator that measures the magnitude of a vector field's source or sink at a given point, in terms of a signed scalar. More technically, the divergence represents the volume density of the outward flux of a vector field from an infinitesimal volume around...
is zero outside the source. This can be generalized to higher dimensions. Generally, for an irrotational vector field in n-dimensional Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
, the intensity "I" of the vector field falls off with the distance "r" following the inverse (n − 1)th power law
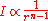 ,
,given that the space outside the source is divergence free.
See also
- FluxFluxIn the various subfields of physics, there exist two common usages of the term flux, both with rigorous mathematical frameworks.* In the study of transport phenomena , flux is defined as flow per unit area, where flow is the movement of some quantity per time...
- Gauss's lawGauss's lawIn physics, Gauss's law, also known as Gauss's flux theorem, is a law relating the distribution of electric charge to the resulting electric field. Gauss's law states that:...
- Kepler's first law
- Telecommunications, particularly:
- William Thomson, 1st Baron Kelvin
- Power-aware routing protocols
- Inverse proportionality
- Multiplicative inverseMultiplicative inverseIn mathematics, a multiplicative inverse or reciprocal for a number x, denoted by 1/x or x−1, is a number which when multiplied by x yields the multiplicative identity, 1. The multiplicative inverse of a fraction a/b is b/a. For the multiplicative inverse of a real number, divide 1 by the...

