Heavy-tailed distribution
Encyclopedia
In probability theory
, heavy-tailed distributions are probability distribution
s whose tails are not exponentially bounded: that is, they have heavier tails than the exponential distribution
. In many applications it is the right tail of the distribution that is of interest, but a distribution may have a heavy left tail, or both tails may be heavy.
There are two important subclasses of heavy-tailed distributions, the long-tailed distributions and the subexponential distributions. In practice, all commonly used heavy-tailed distributions belong to the subexponential class.
There is still some discrepancy over the use of the term heavy-tailed. There are two other definitions in use. Some authors use the term to refer to those distributions which do not have all their power moments finite; and some others to those distributions that do not have a variance
. The definition given in this article is the most general in use, and includes all distributions encompassed by the alternative definitions, as well as those distributions such as log-normal that possess all their power moments, yet which are generally acknowledged to be heavy-tailed. (Occasionally, heavy-tailed is used for any distribution that has heavier tails than the normal distribution.)
X with distribution function
F is said to have a heavy right tail if
This is also written in terms of the tail distribution function
as
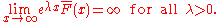
This is equivalent to the statement that the moment generating function of F, MF(t), is infinite for all t > 0.
The definitions of heavy-tailed for left-tailed or two tailed distributions are similar.
X with distribution function
F is said to have a long right tail if for all t > 0,
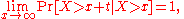
or equivalently
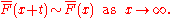
This has the intuitive interpretation for a right-tailed long-tailed distributed quantity that if the long-tailed quantity exceeds some high level, the probability approaches 1 that it will exceed any other higher level: if you know the situation is bad, it is probably worse than you think.
All long-tailed distributions are heavy-tailed, but the converse is false, and it is possible to construct heavy-tailed distributions that are not long-tailed.
s of probability distributions. For two independent, identically distributed random variables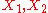
with common distribution function 
the convolution of 
with itself, 
is defined, using Lebesgue-Stieltjes integration
, by:
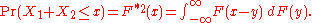
The n-fold convolution
is defined in the same way. The tail
distribution function
is defined as
.
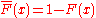A distribution
on the positive half-line is
subexponential if
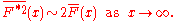
This implies that, for any
,
The probabilistic interpretation of this is that,
for a sum of
independent
random variables
with
common distribution
,
This is often known as the principle of the single big jump.
A distribution
on the whole real line is subexponential if the distribution
is. Here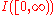 
is the indicator function
of the positive half-line. Alternatively, a random variable
supported on the real line is subexponential if and only if 
is subexponential.
All subexponential distributions are long-tailed, but examples can be constructed of long-tailed distributions that are not subexponential.
Those that are one-tailed include:
Those that are two-tailed include:
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
, heavy-tailed distributions are probability distribution
Probability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
s whose tails are not exponentially bounded: that is, they have heavier tails than the exponential distribution
Exponential distribution
In probability theory and statistics, the exponential distribution is a family of continuous probability distributions. It describes the time between events in a Poisson process, i.e...
. In many applications it is the right tail of the distribution that is of interest, but a distribution may have a heavy left tail, or both tails may be heavy.
There are two important subclasses of heavy-tailed distributions, the long-tailed distributions and the subexponential distributions. In practice, all commonly used heavy-tailed distributions belong to the subexponential class.
There is still some discrepancy over the use of the term heavy-tailed. There are two other definitions in use. Some authors use the term to refer to those distributions which do not have all their power moments finite; and some others to those distributions that do not have a variance
Variance
In probability theory and statistics, the variance is a measure of how far a set of numbers is spread out. It is one of several descriptors of a probability distribution, describing how far the numbers lie from the mean . In particular, the variance is one of the moments of a distribution...
. The definition given in this article is the most general in use, and includes all distributions encompassed by the alternative definitions, as well as those distributions such as log-normal that possess all their power moments, yet which are generally acknowledged to be heavy-tailed. (Occasionally, heavy-tailed is used for any distribution that has heavier tails than the normal distribution.)
Definition of heavy-tailed distribution
The distribution of a random variableRandom variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
X with distribution function
Cumulative distribution function
In probability theory and statistics, the cumulative distribution function , or just distribution function, describes the probability that a real-valued random variable X with a given probability distribution will be found at a value less than or equal to x. Intuitively, it is the "area so far"...
F is said to have a heavy right tail if
This is also written in terms of the tail distribution function
as
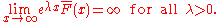
This is equivalent to the statement that the moment generating function of F, MF(t), is infinite for all t > 0.
The definitions of heavy-tailed for left-tailed or two tailed distributions are similar.
Definition of long-tailed distribution
The distribution of a random variableRandom variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
X with distribution function
Cumulative distribution function
In probability theory and statistics, the cumulative distribution function , or just distribution function, describes the probability that a real-valued random variable X with a given probability distribution will be found at a value less than or equal to x. Intuitively, it is the "area so far"...
F is said to have a long right tail if for all t > 0,
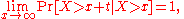
or equivalently
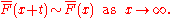
This has the intuitive interpretation for a right-tailed long-tailed distributed quantity that if the long-tailed quantity exceeds some high level, the probability approaches 1 that it will exceed any other higher level: if you know the situation is bad, it is probably worse than you think.
All long-tailed distributions are heavy-tailed, but the converse is false, and it is possible to construct heavy-tailed distributions that are not long-tailed.
Subexponential distributions
Subexponentiality is defined in terms of convolutionConvolution
In mathematics and, in particular, functional analysis, convolution is a mathematical operation on two functions f and g, producing a third function that is typically viewed as a modified version of one of the original functions. Convolution is similar to cross-correlation...
s of probability distributions. For two independent, identically distributed random variables
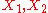with common distribution function the convolution of with itself, is defined, using Lebesgue-Stieltjes integrationLebesgue-Stieltjes integration
In measure-theoretic analysis and related branches of mathematics, Lebesgue–Stieltjes integration generalizes Riemann–Stieltjes and Lebesgue integration, preserving the many advantages of the former in a more general measure-theoretic framework...
, by:
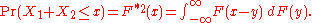
The n-fold convolution
is defined in the same way. The taildistribution function
is defined as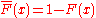.A distribution
on the positive half-line issubexponential if
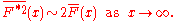
This implies that, for any
,The probabilistic interpretation of this is that,
for a sum of
independentStatistical independence
In probability theory, to say that two events are independent intuitively means that the occurrence of one event makes it neither more nor less probable that the other occurs...
random variables
withcommon distribution
,This is often known as the principle of the single big jump.
A distribution
on the whole real line is subexponential if the distribution is. Here 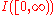is the indicator functionof the positive half-line. Alternatively, a random variable
supported on the real line is subexponential if and only if is subexponential.All subexponential distributions are long-tailed, but examples can be constructed of long-tailed distributions that are not subexponential.
Common heavy-tailed distributions
All commonly used heavy-tailed distributions are subexponential.Those that are one-tailed include:
- the Pareto distribution;
- the Log-normal distribution;
- the Lévy distribution;
- the Weibull distribution with shape parameter less than 1;
- the Burr distribution;
- the Log-gamma distribution;
- the Log-Cauchy distributionLog-Cauchy distributionIn probability theory, a log-Cauchy distribution is a probability distribution of a random variable whose logarithm is distributed in accordance with a Cauchy distribution...
, sometimes described as having a "super-heavy tail" because it exhibits logarithmic decayLogarithmic growthIn mathematics, logarithmic growth describes a phenomenon whose size or cost can be described as a logarithm function of some input. e.g. y = C log . Note that any logarithm base can be used, since one can be converted to another by a fixed constant...
producing a heavier tail than the Pareto distribution.
Those that are two-tailed include:
- The Cauchy distributionCauchy distributionThe Cauchy–Lorentz distribution, named after Augustin Cauchy and Hendrik Lorentz, is a continuous probability distribution. As a probability distribution, it is known as the Cauchy distribution, while among physicists, it is known as the Lorentz distribution, Lorentz function, or Breit–Wigner...
, itself a special case of both the stable distribution and the t-distribution; - The family of stable distributions, excepting the special case of the normal distribution within that family. Some stable distributions are one-sided (or supported by a half-line), see e.g. Lévy distribution. See also financial models with long-tailed distributions and volatility clustering.
- The t-distribution.
- The skew lognormal cascade distribution.