Extreme value theory
Encyclopedia
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
dealing with the extreme deviation
Deviation
Deviation may refer to:* Deviation , the difference between the value of an observation and the mean of the population in mathematics and statistics** Standard deviation, which is based on the square of the difference...
s from the median
Median
In probability theory and statistics, a median is described as the numerical value separating the higher half of a sample, a population, or a probability distribution, from the lower half. The median of a finite list of numbers can be found by arranging all the observations from lowest value to...
of probability distribution
Probability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
s. The general theory sets out to assess the type of probability distributions generated by processes. Extreme value theory is important for assessing risk
Risk
Risk is the potential that a chosen action or activity will lead to a loss . The notion implies that a choice having an influence on the outcome exists . Potential losses themselves may also be called "risks"...
for highly unusual events, such as 100-year flood
100-year flood
A one-hundred-year flood is calculated to be the level of flood water expected to be equaled or exceeded every 100 years on average. The 100-year flood is more accurately referred to as the 1% annual exceedance probability flood, since it is a flood that has a 1% chance of being equaled or exceeded...
s.
Approaches
Two approaches exist today:- Basic theory approach as described in the book by Burry (1975). In general this conforms to the first theorem in extreme value theory (Fisher and Tippett, 1928; Gnedenko, 1943).
- Most common at this moment is the tail-fitting approach based on the second theorem in extreme value theoryPickands–Balkema–de Haan theoremThe Pickands–Balkema–de Haan theorem is often called the second theorem in extreme value theory. It gives the asymptotic tail distribution of a random variable X, when the true distribution F of X is unknown...
(Pickands, 1975; Balkema and de Haan, 1974).
The difference between the two theorems is due to the nature of the data generation. For Theorem I the data are generated in full range, while in Theorem II data is only generated when it surpasses a certain threshold, called Peak Over Threshold models (POT). The POT approach has been developed largely in the insurance business, where only losses (pay outs) above a certain threshold are accessible to the insurance company. Strangely, this approach is often used for cases where Theorem I applies, which creates problems with the basic model assumptions.
Extreme value distributions are the limiting distributions for the minimum or the maximum of a very large collection of independent
Statistical independence
In probability theory, to say that two events are independent intuitively means that the occurrence of one event makes it neither more nor less probable that the other occurs...
random variable
Random variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
s from the same arbitrary distribution. Emil Julius Gumbel
Emil Julius Gumbel
Emil Julius Gumbel was a Jewish mathematician and political writer.Born in Munich, he graduated from the University of Munich shortly before the outbreak of the First World War...
(1958) showed that for any well-behaved initial distribution (i.e., F(x)
Cumulative distribution function
In probability theory and statistics, the cumulative distribution function , or just distribution function, describes the probability that a real-valued random variable X with a given probability distribution will be found at a value less than or equal to x. Intuitively, it is the "area so far"...
is continuous and has an inverse), only a few models are needed, depending on whether you are interested in the maximum or the minimum, and also if the observations are bounded above or below.
Applications
Applications of extreme value theory include predicting the probability distribution of:- Extreme floodFloodA flood is an overflow of an expanse of water that submerges land. The EU Floods directive defines a flood as a temporary covering by water of land not normally covered by water...
s - The amounts of large insuranceInsuranceIn law and economics, insurance is a form of risk management primarily used to hedge against the risk of a contingent, uncertain loss. Insurance is defined as the equitable transfer of the risk of a loss, from one entity to another, in exchange for payment. An insurer is a company selling the...
losses - Equity riskEquity riskEquity risk is the risk that one's investments will depreciate because of stock market dynamics causing one to lose money.The measure of risk used in the equity markets is typically the standard deviation of a security's price over a number of periods...
s - Day to day market riskMarket riskMarket risk is the risk that the value of a portfolio, either an investment portfolio or a trading portfolio, will decrease due to the change in value of the market risk factors. The four standard market risk factors are stock prices, interest rates, foreign exchange rates, and commodity prices...
- The size of freak waveFreak waveRogue waves are relatively large and spontaneous ocean surface waves that occur far out in sea, and are a threat even to large ships and ocean liners...
s - Mutational events during evolutionEvolutionEvolution is any change across successive generations in the heritable characteristics of biological populations. Evolutionary processes give rise to diversity at every level of biological organisation, including species, individual organisms and molecules such as DNA and proteins.Life on Earth...
- Large wildfireWildfireA wildfire is any uncontrolled fire in combustible vegetation that occurs in the countryside or a wilderness area. Other names such as brush fire, bushfire, forest fire, desert fire, grass fire, hill fire, squirrel fire, vegetation fire, veldfire, and wilkjjofire may be used to describe the same...
s - It can be applied to some characterization of the distribution of the maxima of incomes, like in some surveys done in virtually all the National Offices of Statistics
- Estimate fastest time humans are capable of running the 100 metres100 metresThe 100 metres, or 100-metre dash, is a sprint race in track and field competitions. The shortest common outdoor running distance, it is one of the most popular and prestigious events in the sport of athletics. It has been contested at the Summer Olympics since 1896...
sprint. - Pipeline failures due to pitting corrosionPitting corrosionPitting corrosion, or pitting, is a form of extremely localized corrosion that leads to the creation of small holes in the metal. The driving power for pitting corrosion is the depassivation of a small area, which becomes anodic while an unknown but potentially vast area becomes cathodic, leading...
History
The field of extreme value theory was pioneered byLeonard Tippett (1902–1985). Tippett was employed by the British Cotton Industry Research Association, where he worked to make cotton thread stronger. In his studies, he realized that the strength
of a thread was controlled by the strength of its weakest fibers. With the help of R. A. Fisher, Tippet obtained three asymptotic limits describing the distributions of extremes. The German mathematician and anti-Nazi activist Emil Julius Gumbel codified this theory in his 1958 book Statistics of Extremes, including the Gumbel distributions that bear his name.
A summary of historically important publications relating to extreme values theory can be found on the article List of publications in statistics.
Classical extreme value theory and models
Let
be a sequence of independent and identically distributed variables with distribution function F and let 
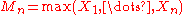denote the maximum.In theory, the exact distribution of the maximum can be derived:
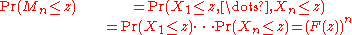
In practice, we might not have the distribution function
but the Fisher–Tippett–Gnedenko theorem provides the following asymptotic resultIf there exist sequences of constants
and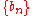 
such that
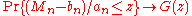as 
and G is a non-degenerate distribution then 
belongs to one of the following families:
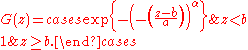
where
.See also
- Generalized extreme value distribution
- Pareto distribution
- Large deviation theory
- Weibull distribution
- Extreme riskExtreme riskExtreme risks are risks of very bad outcomes or "high consequence", but of low probability. They include the risks of terrorist attack,biosecurity risks such as the invasion of pests, and extreme natural disasters such as major earthquakes.-Introduction:...
- Extreme weatherExtreme weatherExtreme weather includes weather phenomena that are at the extremes of the historical distribution, especially severe or unseasonal weather. The most commonly used definition of extreme weather is based on an event's climatological distribution. Extreme weather occurs only 5% or less of the time...
- Fisher–Tippett–Gnedenko theorem