Tweedie distributions
Encyclopedia
In probability
and statistics
, the Tweedie distributions are a family of probability distribution
s which include continuous distributions such as the normal and gamma, the purely discrete scaled Poisson distribution
, and the class of mixed compound Poisson-Gamma distributions which have positive mass at zero, but are otherwise continuous.
The Tweedie distributions were so named by Bent Jørgensen after Maurice Charles Kenneth Tweedie, a medical statistician at the University of Liverpool
, UK, who presented the first thorough study of these distributions in 1984.
which has a probability density function
of the form:
.
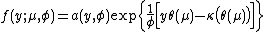For a Tweedie distribution, θ and κ are of the form:
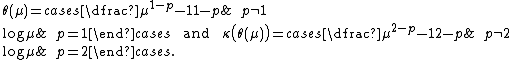
μ and variance
φμp,where φ > 0 is a dispersion
parameter, and p, called the index parameter, (uniquely) determines the distribution in the Tweedie family.
Special cases include:
Tweedie distributions exist for all real values of p except for 0 < p < 1.
Apart from the four special cases identified above, their probability density function have no closed form. However, software is available that enables the accurate computation of the Tweedie densities (and probability distribution functions).
The index parameter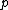
defines the type of distribution:
s.
Applications of Tweedie distributions (apart from the four special cases identified) include:
Probability
Probability is ordinarily used to describe an attitude of mind towards some proposition of whose truth we arenot certain. The proposition of interest is usually of the form "Will a specific event occur?" The attitude of mind is of the form "How certain are we that the event will occur?" The...
and statistics
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, the Tweedie distributions are a family of probability distribution
Probability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
s which include continuous distributions such as the normal and gamma, the purely discrete scaled Poisson distribution
Poisson distribution
In probability theory and statistics, the Poisson distribution is a discrete probability distribution that expresses the probability of a given number of events occurring in a fixed interval of time and/or space if these events occur with a known average rate and independently of the time since...
, and the class of mixed compound Poisson-Gamma distributions which have positive mass at zero, but are otherwise continuous.
The Tweedie distributions were so named by Bent Jørgensen after Maurice Charles Kenneth Tweedie, a medical statistician at the University of Liverpool
University of Liverpool
The University of Liverpool is a teaching and research university in the city of Liverpool, England. It is a member of the Russell Group of large research-intensive universities and the N8 Group for research collaboration. Founded in 1881 , it is also one of the six original "red brick" civic...
, UK, who presented the first thorough study of these distributions in 1984.
Definition
Tweedie distributions are a special case of an exponential dispersion model, a type of exponential familyExponential family
In probability and statistics, an exponential family is an important class of probability distributions sharing a certain form, specified below. This special form is chosen for mathematical convenience, on account of some useful algebraic properties, as well as for generality, as exponential...
which has a probability density function
Probability density function
In probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...
of the form:
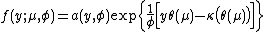.For a Tweedie distribution, θ and κ are of the form:
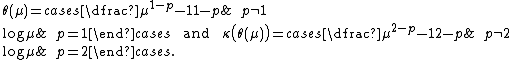
Properties
Such a distribution will have meanExpected value
In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
μ and variance
Variance
In probability theory and statistics, the variance is a measure of how far a set of numbers is spread out. It is one of several descriptors of a probability distribution, describing how far the numbers lie from the mean . In particular, the variance is one of the moments of a distribution...
φμp,where φ > 0 is a dispersion
Statistical dispersion
In statistics, statistical dispersion is variability or spread in a variable or a probability distribution...
parameter, and p, called the index parameter, (uniquely) determines the distribution in the Tweedie family.
Special cases include:
-
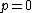, which is the normal distribution -
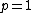with 
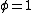, which is the Poisson distributionPoisson distributionIn probability theory and statistics, the Poisson distribution is a discrete probability distribution that expresses the probability of a given number of events occurring in a fixed interval of time and/or space if these events occur with a known average rate and independently of the time since... -
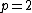, which is the gamma distribution -
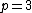, which is the inverse Gaussian distributionInverse Gaussian distribution| cdf = \Phi\left +\exp\left \Phi\left...
.
Tweedie distributions exist for all real values of p except for 0 < p < 1.
Apart from the four special cases identified above, their probability density function have no closed form. However, software is available that enables the accurate computation of the Tweedie densities (and probability distribution functions).
The index parameter
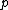defines the type of distribution:
- For
, the data 
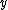are supported on the whole real line (but, interestingly, 
). Applications for these distributions are unknown. - For
(the normal distribution), the data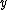 
and the mean 
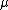are supported on the whole real line. - For
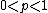, no distributions exist - For
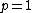, the distribution exists on the non-negative integers - For
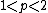, the distributions are continuous on the positive reals, plus an added mass (exact zero) at 
. For example, consider monthly rainfall. When no rain is recorded, an exact zero is recorded. If rain is recorded, a continuous amount results. These distributions are also called the Poisson-gamma distributions, since they can be represented as the Poisson sum of gamma distributions. They are therefore a type of compound Poisson distributionCompound Poisson distributionIn probability theory, a compound Poisson distribution is the probability distribution of the sum of a "Poisson-distributed number" of independent identically-distributed random variables...
. - For
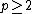, the data 
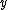are supported on the non-negative reals, and 
. These distribution are like the gamma distribution (which corresponds to 
), but are progressively more right-skewed as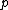 
gets larger.
Applications
Tweedie distributions usually arise as the response distributions for generalized linear modelGeneralized linear model
In statistics, the generalized linear model is a flexible generalization of ordinary linear regression. The GLM generalizes linear regression by allowing the linear model to be related to the response variable via a link function and by allowing the magnitude of the variance of each measurement to...
s.
Applications of Tweedie distributions (apart from the four special cases identified) include:
- actuarial studies
- assay analysis
- survival analysis
- ecology
- analysis of alcohol consumption in British teenagers
- medical applications
- meteorology and climatology
- fisheries
Further reading
- Kaas, R. (2005). Compound Poisson distribution and GLM’s – Tweedie’s distribution. In Proceedings of the Contact Forum "3rd Actuarial and Financial Mathematics Day", pages 3–12. Brussels: Royal Flemish Academy of Belgium for Science and the Arts. http://ucs.kuleuven.be/seminars_events/other/files/3afmd/Kaas.PDF
- Ohlsson, E and Johansson, B. Exact Credibility and Tweedie Models, University of Stockholm, Research report, October 2003. http://www.math.su.se/matstat/reports/seriea/2003/rep15/report.pdf
- Tweedie, M.C.K. (1956). Some statistical properties of inverse Gaussian distributions. Virginia J. Sci. (N.S.) 7 (1956), 160—165.
- Tweedie distributions. http://www.statsci.org/s/tweedie.html
- Tweedie generalized linear model family. http://www.statsci.org/s/tweedief.html
- Examples of use of the model. http://www.sci.usq.edu.au/staff/dunn/Datasets/tech-glms.html#Tweedie