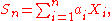Moment-generating function
Encyclopedia
In probability theory
and statistics
, the moment-generating function of any random variable
is an alternative definition of its probability distribution
. Thus, it provides the basis of an alternative route to analytical results compared with working directly with probability density function
s or cumulative distribution function
s. There are particularly simple results for the moment-generating functions of distributions defined by the weighted sums of random variables.
In addition to univariate distributions, moment-generating functions can be defined for vector- or matrix-valued random variables, and can even be extended to more general cases.
The moment-generating function does not always exist even for real-valued arguments, unlike the characteristic function
. There are relations between the behavior of the moment-generating function of a distribution and properties of the distribution, such as the existence of moments.
and statistics
, the moment-generating function of a random variable
X is
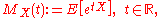
wherever this expectation
exists.
 always exists and is equal to 1.
always exists and is equal to 1.
A key problem with moment-generating functions is that moments and the moment-generating function may not exist, as the integrals need not converge absolutely. By contrast, the characteristic function
always exists (because it is the integral of a bounded function on a space of finite measure), and thus may be used instead.
More generally, where , an n-dimensional random vector, one uses
, an n-dimensional random vector, one uses  instead of tX:
instead of tX:

Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
and statistics
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, the moment-generating function of any random variable
Random variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
is an alternative definition of its probability distribution
Probability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
. Thus, it provides the basis of an alternative route to analytical results compared with working directly with probability density function
Probability density function
In probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...
s or cumulative distribution function
Cumulative distribution function
In probability theory and statistics, the cumulative distribution function , or just distribution function, describes the probability that a real-valued random variable X with a given probability distribution will be found at a value less than or equal to x. Intuitively, it is the "area so far"...
s. There are particularly simple results for the moment-generating functions of distributions defined by the weighted sums of random variables.
In addition to univariate distributions, moment-generating functions can be defined for vector- or matrix-valued random variables, and can even be extended to more general cases.
The moment-generating function does not always exist even for real-valued arguments, unlike the characteristic function
Characteristic function (probability theory)
In probability theory and statistics, the characteristic function of any random variable completely defines its probability distribution. Thus it provides the basis of an alternative route to analytical results compared with working directly with probability density functions or cumulative...
. There are relations between the behavior of the moment-generating function of a distribution and properties of the distribution, such as the existence of moments.
Definition
In probability theoryProbability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
and statistics
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
, the moment-generating function of a random variable
Random variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
X is
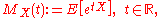
wherever this expectation
Expected value
In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
exists.
 always exists and is equal to 1.
always exists and is equal to 1.A key problem with moment-generating functions is that moments and the moment-generating function may not exist, as the integrals need not converge absolutely. By contrast, the characteristic function
Characteristic function (probability theory)
In probability theory and statistics, the characteristic function of any random variable completely defines its probability distribution. Thus it provides the basis of an alternative route to analytical results compared with working directly with probability density functions or cumulative...
always exists (because it is the integral of a bounded function on a space of finite measure), and thus may be used instead.
More generally, where
 , an n-dimensional random vector, one uses
, an n-dimensional random vector, one uses  instead of tX:
instead of tX:
Why the moment-generating function is defined this way
The reason for defining this function is that it can be used to find all the moments of the distribution. The series expansion of etX is-

Hence
-

where mi is the ith momentMoment (mathematics)In mathematics, a moment is, loosely speaking, a quantitative measure of the shape of a set of points. The "second moment", for example, is widely used and measures the "width" of a set of points in one dimension or in higher dimensions measures the shape of a cloud of points as it could be fit by...
.
If we differentiate MX(t) i times with respect to t and then set t = 0 we shall therefore obtain the ith moment about the origin, mi. This is summarized more compactly below in the section entitled "Calculations of moments."
Examples
Distribution Moment-generating function MX(t) Characteristic function φ(t) Bernoulli 


Geometric 
 , for
, for 

Binomial B(n, p) 

Poisson Poisson distributionIn probability theory and statistics, the Poisson distribution is a discrete probability distribution that expresses the probability of a given number of events occurring in a fixed interval of time and/or space if these events occur with a known average rate and independently of the time since...
Pois(λ)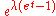

Uniform Uniform distribution (continuous)In probability theory and statistics, the continuous uniform distribution or rectangular distribution is a family of probability distributions such that for each member of the family, all intervals of the same length on the distribution's support are equally probable. The support is defined by...
U(a, b)
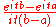
Normal N(μ, σ2) 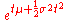
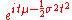
Chi-squared χ2k 

Gamma Γ(k, θ) 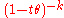
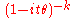
Exponential Exponential distributionIn probability theory and statistics, the exponential distribution is a family of continuous probability distributions. It describes the time between events in a Poisson process, i.e...
Exp(λ)

Multivariate normal N(μ, Σ) 
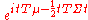
Degenerate δa 
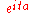
Laplace L(μ, b) 
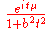
Cauchy Cauchy distributionThe Cauchy–Lorentz distribution, named after Augustin Cauchy and Hendrik Lorentz, is a continuous probability distribution. As a probability distribution, it is known as the Cauchy distribution, while among physicists, it is known as the Lorentz distribution, Lorentz function, or Breit–Wigner...
Cauchy(μ, θ)not defined
|-
| Negative BinomialNegative binomial distributionIn probability theory and statistics, the negative binomial distribution is a discrete probability distribution of the number of successes in a sequence of Bernoulli trials before a specified number of failures occur...
NB(r, p)
|
|
|-
|}
Calculation
The moment-generating function is given by the Riemann–Stieltjes integral
where F is the cumulative distribution functionCumulative distribution functionIn probability theory and statistics, the cumulative distribution function , or just distribution function, describes the probability that a real-valued random variable X with a given probability distribution will be found at a value less than or equal to x. Intuitively, it is the "area so far"...
.
If X has a continuous probability density functionProbability density functionIn probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...
ƒ(x), then MX(−t) is the two-sided Laplace transformTwo-sided Laplace transformIn mathematics, the two-sided Laplace transform or bilateral Laplace transform is an integral transform closely related to the Fourier transform, the Mellin transform, and the ordinary or one-sided Laplace transform...
of ƒ(x).
-

where mi is the ith momentMoment (mathematics)In mathematics, a moment is, loosely speaking, a quantitative measure of the shape of a set of points. The "second moment", for example, is widely used and measures the "width" of a set of points in one dimension or in higher dimensions measures the shape of a cloud of points as it could be fit by...
.
Sum of independent random variables
If X1, X2, ..., Xn is a sequence of independent (and not necessarily identically distributed) random variables, and
where the ai are constants, then the probability density function for Sn is the convolutionConvolutionIn mathematics and, in particular, functional analysis, convolution is a mathematical operation on two functions f and g, producing a third function that is typically viewed as a modified version of one of the original functions. Convolution is similar to cross-correlation...
of the probability density functions of each of the Xi, and the moment-generating function for Sn is given by
-
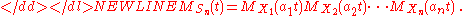
Vector-valued random variables
For vector-valued random variables X with realReal numberIn mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
components, the moment-generating function is given by

where t is a vector and is the dot productDot productIn mathematics, the dot product or scalar product is an algebraic operation that takes two equal-length sequences of numbers and returns a single number obtained by multiplying corresponding entries and then summing those products...
is the dot productDot productIn mathematics, the dot product or scalar product is an algebraic operation that takes two equal-length sequences of numbers and returns a single number obtained by multiplying corresponding entries and then summing those products...
.
Important properties
The most important property of the moment-generating function is that if two distributions have the same moment-generating function, then they are identical at all points. That is, if for all values of t,
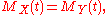
then
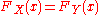
for all values of x (or equivalently X and Y have the same distribution). This statement is not equivalent to ``if two distributions have the same moments, then they are identical at all points", because in some cases the moments exist and yet the moment-generating function does not, because in some cases the limit

does not exist. This happens for the lognormal distribution.
Calculations of moments
The moment-generating function is so called because if it exists on an open interval around t = 0, then it is the exponential generating function of the momentsMoment (mathematics)In mathematics, a moment is, loosely speaking, a quantitative measure of the shape of a set of points. The "second moment", for example, is widely used and measures the "width" of a set of points in one dimension or in higher dimensions measures the shape of a cloud of points as it could be fit by...
of the probability distributionProbability distributionIn probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
:
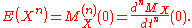
n should be nonnegative.
Other properties
Hoeffding's lemmaHoeffding's lemmaIn probability theory, Hoeffding's lemma is an inequality that bounds the moment-generating function of any bounded random variable. It is named after the Finnish–American mathematical statistician Wassily Hoeffding....
provides a bound on the moment-generating function in the case of a zero-mean, bounded random variable.
Relation to other functions
Related to the moment-generating function are a number of other transforms that are common in probability theory:
characteristic functionCharacteristic function (probability theory)In probability theory and statistics, the characteristic function of any random variable completely defines its probability distribution. Thus it provides the basis of an alternative route to analytical results compared with working directly with probability density functions or cumulative...
: The characteristic functionCharacteristic function (probability theory)In probability theory and statistics, the characteristic function of any random variable completely defines its probability distribution. Thus it provides the basis of an alternative route to analytical results compared with working directly with probability density functions or cumulative...
 is related to the moment-generating function via
is related to the moment-generating function via  the characteristic function is the moment-generating function of iX or the moment generating function of X evaluated on the imaginary axis. This function can also be viewed as the Fourier transformFourier transformIn mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...
the characteristic function is the moment-generating function of iX or the moment generating function of X evaluated on the imaginary axis. This function can also be viewed as the Fourier transformFourier transformIn mathematics, Fourier analysis is a subject area which grew from the study of Fourier series. The subject began with the study of the way general functions may be represented by sums of simpler trigonometric functions...
of the probability density functionProbability density functionIn probability theory, a probability density function , or density of a continuous random variable is a function that describes the relative likelihood for this random variable to occur at a given point. The probability for the random variable to fall within a particular region is given by the...
, which can therefore be deduced from it by inverse Fourier transform.
cumulant-generating function: The cumulant-generating function is defined as the logarithm of the moment-generating function; some instead define the cumulant-generating function as the logarithm of the characteristic functionCharacteristic function (probability theory)In probability theory and statistics, the characteristic function of any random variable completely defines its probability distribution. Thus it provides the basis of an alternative route to analytical results compared with working directly with probability density functions or cumulative...
, while others call this latter the second cumulant-generating function.
probability-generating functionProbability-generating functionIn probability theory, the probability-generating function of a discrete random variable is a power series representation of the probability mass function of the random variable...
: The probability-generating functionProbability-generating functionIn probability theory, the probability-generating function of a discrete random variable is a power series representation of the probability mass function of the random variable...
is defined as This immediately implies that
This immediately implies that 
See also
- Factorial moment generating function
- Rate functionRate functionIn mathematics — specifically, in large deviations theory — a rate function is a function used to quantify the probabilities of rare events. It is required to have several "nice" properties which assist in the formulation of the large deviation principle...
-
-
-