Rejection sampling
Encyclopedia
In mathematics
, rejection sampling is a basic pseudo-random number sampling
technique used to generate observations from a distribution
. It is also commonly called the acceptance-rejection method or "accept-reject algorithm".
It generates sampling values from an arbitrary probability distribution
function
by using an instrumental distribution 
, under the only restriction that 
where 
is an appropriate bound on 
.
Rejection sampling is usually used in cases where the form of
makes sampling difficult. Instead of sampling directly from the distribution 
, we use an envelope distribution 
where sampling is easier. These samples from 
are probabilistically accepted or rejected.
This method relates to the general field of Monte Carlo
techniques, including Markov chain Monte Carlo
algorithms that also use a proxy distribution to achieve simulation from the target distribution
. It forms the basis for algorithms such as the Metropolis algorithm.
The unconditional acceptance probability is the proportion of proposed samples which are accepted, which is
∫
∫
. If 
is low, fewer samples are rejected, and the required number of samples for the target distribution is obtained more quickly. Because 
must be no less than the maximum of 
, the unconditional acceptance probability is higher the less that ratio varies, however to obtain acceptance probability 1, 
, which defeats the purpose of sampling.
and dating back to Buffon and his needle
) is as follows:
The validation of this method is the envelope principle: when simulating the pair
, one produces a uniform simulation over the subgraph of 
. Accepting only pairs such that 
then produces pairs 
uniformly distributed over the subgraph of 
and thus, marginally, a simulation from 
.
This means that, with enough replicates, the algorithm generates a sample from the desired distribution
. There are a number of extensions to this algorithm, such as the Metropolis algorithm.
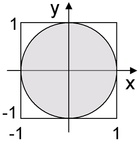As a simple geometric example, suppose it is desired to generate a random point within the unit circle. Generate a candidate point 
where 
and 
are independent uniformly distributed between −1 and 1. If it so happens that 
then the point is within the unit circle and should be accepted. If not then this point should be rejected and another candidate should be generated.
The ziggurat algorithm
, a more advanced example, is used to efficiently generate normally-distributed pseudorandom numbers.
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, rejection sampling is a basic pseudo-random number sampling
Pseudo-random number sampling
Pseudo-random number sampling or non-uniform pseudo-random variate generation is the numerical practice of generating pseudo-random numbers that are distributed according to a given probability distribution....
technique used to generate observations from a distribution
Probability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
. It is also commonly called the acceptance-rejection method or "accept-reject algorithm".
It generates sampling values from an arbitrary probability distribution
Probability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
function
by using an instrumental distribution , under the only restriction that where is an appropriate bound on .Rejection sampling is usually used in cases where the form of
makes sampling difficult. Instead of sampling directly from the distribution , we use an envelope distribution where sampling is easier. These samples from are probabilistically accepted or rejected.This method relates to the general field of Monte Carlo
Monte Carlo method
Monte Carlo methods are a class of computational algorithms that rely on repeated random sampling to compute their results. Monte Carlo methods are often used in computer simulations of physical and mathematical systems...
techniques, including Markov chain Monte Carlo
Markov chain Monte Carlo
Markov chain Monte Carlo methods are a class of algorithms for sampling from probability distributions based on constructing a Markov chain that has the desired distribution as its equilibrium distribution. The state of the chain after a large number of steps is then used as a sample of the...
algorithms that also use a proxy distribution to achieve simulation from the target distribution
. It forms the basis for algorithms such as the Metropolis algorithm.The unconditional acceptance probability is the proportion of proposed samples which are accepted, which is
∫∫. If is low, fewer samples are rejected, and the required number of samples for the target distribution is obtained more quickly. Because must be no less than the maximum of , the unconditional acceptance probability is higher the less that ratio varies, however to obtain acceptance probability 1, , which defeats the purpose of sampling.Algorithm
The algorithm (used by John von NeumannJohn von Neumann
John von Neumann was a Hungarian-American mathematician and polymath who made major contributions to a vast number of fields, including set theory, functional analysis, quantum mechanics, ergodic theory, geometry, fluid dynamics, economics and game theory, computer science, numerical analysis,...
and dating back to Buffon and his needle
Buffon's needle
In mathematics, Buffon's needle problem is a question first posed in the 18th century by Georges-Louis Leclerc, Comte de Buffon:Buffon's needle was the earliest problem in geometric probability to be solved; it can be solved using integral geometry...
) is as follows:
- Sample
from 
and 
from 
(the uniform distribution over the unit interval) - Check whether or not
.
- If this holds, accept
as a realization of 
; - if not, reject the value of
and repeat the sampling step.
- If this holds, accept
The validation of this method is the envelope principle: when simulating the pair
, one produces a uniform simulation over the subgraph of . Accepting only pairs such that then produces pairs uniformly distributed over the subgraph of and thus, marginally, a simulation from .This means that, with enough replicates, the algorithm generates a sample from the desired distribution
. There are a number of extensions to this algorithm, such as the Metropolis algorithm.Examples
where and are independent uniformly distributed between −1 and 1. If it so happens that then the point is within the unit circle and should be accepted. If not then this point should be rejected and another candidate should be generated.The ziggurat algorithm
Ziggurat algorithm
The ziggurat algorithm is an algorithm for pseudo-random number sampling. Belonging to the class of rejection sampling algorithms, it relies on an underlying source of uniformly-distributed random numbers, typically from a pseudo-random number generator, as well as precomputed tables. The...
, a more advanced example, is used to efficiently generate normally-distributed pseudorandom numbers.
Drawbacks
Rejection sampling can lead to a lot of unwanted samples being taken if the function being sampled is highly concentrated in a certain region, for example a function that has a spike at some location. Also, as the dimensions of the problem get larger, the ratio of the embedded volume to the "corners" of the embedding volume tends towards zero, thus a lot of rejections can take place before a useful sample is generated, thus making the algorithm inefficient and impractical. See curse of dimensionalityCurse of dimensionality
The curse of dimensionality refers to various phenomena that arise when analyzing and organizing high-dimensional spaces that do not occur in low-dimensional settings such as the physical space commonly modeled with just three dimensions.There are multiple phenomena referred to by this name in...
.