Renewal theory
Encyclopedia
Renewal theory is the branch of probability theory
that generalizes Poisson processes for arbitrary holding times. Applications include calculating the expected time for a monkey who is randomly tapping at a keyboard
to type the word Macbeth and comparing the long-term benefits of different insurance policies.
. In essence, the Poisson process is a continuous-time Markov process on the positive integers (usually starting at zero) which has independent identically distributed holding times at each integer (exponentially distributed)
(exponentially distributed)
before advancing (with probability 1) to the next integer: . In the same informal spirit, we may define a renewal process to be the same thing, except that the holding times take on a more general distribution. (Note however that the independence and identical distribution (IID) property of the holding times is retained).
. In the same informal spirit, we may define a renewal process to be the same thing, except that the holding times take on a more general distribution. (Note however that the independence and identical distribution (IID) property of the holding times is retained).
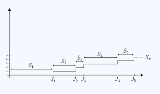
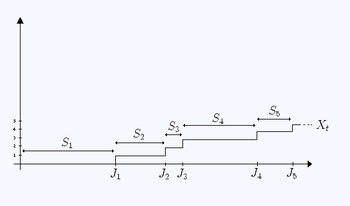 Let
Let  be a sequence of positive independent identically distributed random variable
be a sequence of positive independent identically distributed random variable
s such that

We refer to the random variable as the "
as the " th" holding time.
th" holding time.
Define for each n > 0 :

each referred to as the "
referred to as the " th" jump time and the intervals
th" jump time and the intervals

being called renewal intervals.
Then the random variable given by
given by

(where is the indicator function) represents the number of jumps that have occurred by time t, and is called a renewal process.
is the indicator function) represents the number of jumps that have occurred by time t, and is called a renewal process.
 as the time elapsed before a machine breaks for the "
as the time elapsed before a machine breaks for the " th" time since the last time it broke. (Note this assumes that the machine is immediately fixed and we restart the clock immediately.) Under this interpretation, the jump times
th" time since the last time it broke. (Note this assumes that the machine is immediately fixed and we restart the clock immediately.) Under this interpretation, the jump times  record the successive times at which the machine breaks and the renewal process
record the successive times at which the machine breaks and the renewal process  records the number of times the machine has so far had to be repaired at any given time
records the number of times the machine has so far had to be repaired at any given time  .
.
However it is more helpful to understand the renewal process in its abstract form, since it may be used to model a great number of practical situations of interest which do not relate very closely to the operation of machines.
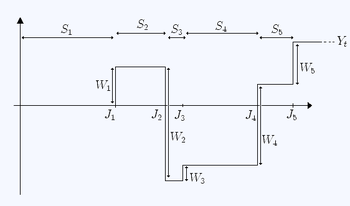 Let
Let  be a sequence of IID random variables (rewards) satisfying
be a sequence of IID random variables (rewards) satisfying

Then the random variable

is called a renewal-reward process. Note that unlike the , each
, each  may take negative values as well as positive values.
may take negative values as well as positive values.
The random variable depends on two sequences: the holding times
depends on two sequences: the holding times  and the rewards
and the rewards
 These two sequences need not be independent. In particular,
These two sequences need not be independent. In particular,  may be a function
may be a function
of .
.
 (which in this case happen to be negative) may be viewed as the successive repair costs incurred as a result of the successive malfunctions.
(which in this case happen to be negative) may be viewed as the successive repair costs incurred as a result of the successive malfunctions.
An alternative analogy is that we have a magic goose which lays eggs at intervals (holding times) distributed as . Sometimes it lays golden eggs of random weight, and sometimes it lays toxic eggs (also of random weight) which require responsible (and costly) disposal. The "rewards"
. Sometimes it lays golden eggs of random weight, and sometimes it lays toxic eggs (also of random weight) which require responsible (and costly) disposal. The "rewards"  are the successive (random) financial losses/gains resulting from successive eggs (i = 1,2,3,...) and
are the successive (random) financial losses/gains resulting from successive eggs (i = 1,2,3,...) and  records the total financial "reward" at time t.
records the total financial "reward" at time t.



To prove the elementary renewal theorem, it is sufficient to show that is uniformly integrable.
is uniformly integrable.
To do this, consider some truncated renewal process where the holding times are defined by where
where  is a point such that
is a point such that  which exists for all non-deterministic renewal processes. This new renewal process
which exists for all non-deterministic renewal processes. This new renewal process  is an upper bound on
is an upper bound on  and its renewals can only occur on the lattice
and its renewals can only occur on the lattice  . Furthermore, the number of renewals at each time is geometric with parameter
. Furthermore, the number of renewals at each time is geometric with parameter  . So we have
. So we have


The reward function satisfies


where is the cumulative distribution function of
is the cumulative distribution function of  and
and  is the corresponding probability density function.
is the corresponding probability density function.
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
that generalizes Poisson processes for arbitrary holding times. Applications include calculating the expected time for a monkey who is randomly tapping at a keyboard
Infinite monkey theorem
The infinite monkey theorem states that a monkey hitting keys at random on a typewriter keyboard for an infinite amount of time will almost surely type a given text, such as the complete works of William Shakespeare....
to type the word Macbeth and comparing the long-term benefits of different insurance policies.
Introduction
A renewal process is a generalization of the Poisson processPoisson process
A Poisson process, named after the French mathematician Siméon-Denis Poisson , is a stochastic process in which events occur continuously and independently of one another...
. In essence, the Poisson process is a continuous-time Markov process on the positive integers (usually starting at zero) which has independent identically distributed holding times at each integer
 (exponentially distributed)
(exponentially distributed)Exponential distribution
In probability theory and statistics, the exponential distribution is a family of continuous probability distributions. It describes the time between events in a Poisson process, i.e...
before advancing (with probability 1) to the next integer:
 . In the same informal spirit, we may define a renewal process to be the same thing, except that the holding times take on a more general distribution. (Note however that the independence and identical distribution (IID) property of the holding times is retained).
. In the same informal spirit, we may define a renewal process to be the same thing, except that the holding times take on a more general distribution. (Note however that the independence and identical distribution (IID) property of the holding times is retained).Formal definition

 be a sequence of positive independent identically distributed random variable
be a sequence of positive independent identically distributed random variableRandom variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
s such that

We refer to the random variable
 as the "
as the " th" holding time.
th" holding time.Define for each n > 0 :

each
 referred to as the "
referred to as the " th" jump time and the intervals
th" jump time and the intervals
being called renewal intervals.
Then the random variable
 given by
given by
(where
 is the indicator function) represents the number of jumps that have occurred by time t, and is called a renewal process.
is the indicator function) represents the number of jumps that have occurred by time t, and is called a renewal process.Interpretation
One may choose to think of the holding times as the time elapsed before a machine breaks for the "
as the time elapsed before a machine breaks for the " th" time since the last time it broke. (Note this assumes that the machine is immediately fixed and we restart the clock immediately.) Under this interpretation, the jump times
th" time since the last time it broke. (Note this assumes that the machine is immediately fixed and we restart the clock immediately.) Under this interpretation, the jump times  record the successive times at which the machine breaks and the renewal process
record the successive times at which the machine breaks and the renewal process  records the number of times the machine has so far had to be repaired at any given time
records the number of times the machine has so far had to be repaired at any given time  .
.However it is more helpful to understand the renewal process in its abstract form, since it may be used to model a great number of practical situations of interest which do not relate very closely to the operation of machines.
Renewal-reward processes

 be a sequence of IID random variables (rewards) satisfying
be a sequence of IID random variables (rewards) satisfying
Then the random variable

is called a renewal-reward process. Note that unlike the
 , each
, each  may take negative values as well as positive values.
may take negative values as well as positive values.The random variable
 depends on two sequences: the holding times
depends on two sequences: the holding times  and the rewards
and the rewards These two sequences need not be independent. In particular,
These two sequences need not be independent. In particular,  may be a function
may be a functionof
 .
.Interpretation
In the context of the above interpretation of the holding times as the time between successive malfunctions of a machine, the "rewards" (which in this case happen to be negative) may be viewed as the successive repair costs incurred as a result of the successive malfunctions.
(which in this case happen to be negative) may be viewed as the successive repair costs incurred as a result of the successive malfunctions.An alternative analogy is that we have a magic goose which lays eggs at intervals (holding times) distributed as
 . Sometimes it lays golden eggs of random weight, and sometimes it lays toxic eggs (also of random weight) which require responsible (and costly) disposal. The "rewards"
. Sometimes it lays golden eggs of random weight, and sometimes it lays toxic eggs (also of random weight) which require responsible (and costly) disposal. The "rewards"  are the successive (random) financial losses/gains resulting from successive eggs (i = 1,2,3,...) and
are the successive (random) financial losses/gains resulting from successive eggs (i = 1,2,3,...) and  records the total financial "reward" at time t.
records the total financial "reward" at time t.Properties of renewal processes and renewal-reward processes
We define the renewal function:
The elementary renewal theorem
The renewal function satisfies
Proof
Below, you find that the strong law of large numbers for renewal processes tell us that
To prove the elementary renewal theorem, it is sufficient to show that
 is uniformly integrable.
is uniformly integrable.To do this, consider some truncated renewal process where the holding times are defined by
 where
where  is a point such that
is a point such that  which exists for all non-deterministic renewal processes. This new renewal process
which exists for all non-deterministic renewal processes. This new renewal process  is an upper bound on
is an upper bound on  and its renewals can only occur on the lattice
and its renewals can only occur on the lattice  . Furthermore, the number of renewals at each time is geometric with parameter
. Furthermore, the number of renewals at each time is geometric with parameter  . So we have
. So we have
The elementary renewal theorem for renewal reward processes
We define the reward function:
The reward function satisfies

The renewal equation
The renewal function satisfies
where
 is the cumulative distribution function of
is the cumulative distribution function of  and
and  is the corresponding probability density function.
is the corresponding probability density function.Proof of the renewal equation
- We may iterate the expectation about the first holding time:
- But by the Markov propertyMarkov propertyIn probability theory and statistics, the term Markov property refers to the memoryless property of a stochastic process. It was named after the Russian mathematician Andrey Markov....
-

- as required.
Asymptotic properties
 and
and  satisfy
satisfy
 (strong law of large numbersLaw of large numbersIn probability theory, the law of large numbers is a theorem that describes the result of performing the same experiment a large number of times...
(strong law of large numbersLaw of large numbersIn probability theory, the law of large numbers is a theorem that describes the result of performing the same experiment a large number of times...
for renewal processes)
 (strong law of large numbers for renewal-reward processes)
(strong law of large numbers for renewal-reward processes)
almost surely.
Proof
- First consider
 . By definition we have:
. By definition we have:
- for all
 and so
and so
-

- for all t ≥ 0.
- Now since
 we have:
we have:
- as
 almost surelyAlmost surelyIn probability theory, one says that an event happens almost surely if it happens with probability one. The concept is analogous to the concept of "almost everywhere" in measure theory...
almost surelyAlmost surelyIn probability theory, one says that an event happens almost surely if it happens with probability one. The concept is analogous to the concept of "almost everywhere" in measure theory...
(with probability 1). Hence:
- almost surely (using the strong law of large numbers); similarly:
- almost surely.
- Thus (since
 is sandwiched between the two terms)
is sandwiched between the two terms)
-

- almost surely.
- Next consider
 . We have
. We have
- almost surely (using the first result and using the law of large numbers on
 ).
).
The inspection paradox
A curious feature of renewal processes is that if we wait some predetermined time t and then observe how large the renewal interval containing t is, we should expect it to be typically larger than a renewal interval of average size.
Mathematically the inspection paradox states: for any t > 0 the renewal interval containing t is stochastically larger than the first renewal interval. That is, for all x > 0 and for all t > 0:

where FS is the cumulative distribution function of the IID holding times Si.
Proof of the inspection paradox
Observe that the last jump-time before t is
 ; and that the renewal interval containing t is
; and that the renewal interval containing t is  . Then
. Then

as required.
Example 1: use of the strong law of large numbers
Eric the entrepreneur has n machines, each having an operational lifetime uniformly distributed between zero and two years. Eric may let each machine run until it fails with replacement cost €2600; alternatively he may replace a machine at any time while it is still functional at a cost of €200.
What is his optimal replacement policy?
Solution
We may model the lifetime of the n machines as n independent concurrent renewal-reward processes, so it is sufficient to consider the case n=1. Denote this process by . The successive lifetimes S of the replacement machines are independent and identically distributed, so the optimal policy is the same for all replacement machines in the process.
. The successive lifetimes S of the replacement machines are independent and identically distributed, so the optimal policy is the same for all replacement machines in the process.
If Eric decides at the start of a machine's life to replace it at time 0 < t < 2 but the machine happens to fail before that time then the lifetime S of the machine is uniformly distributed on [0, t] and thus has expectation 0.5t. So the overall expected lifetime of the machine is:

and the expected cost W per machine is:

So by the strong law of large numbers, his long-term average cost per unit time is:

then differentiating with respect to t:

this implies that the turning points satisfy:

and thus

We take the only solution t in [0, 2]: t = 2/3. This is indeed a minimum (and not a maximum) since the cost per unit time tends to infinity as t tends to zero, meaning that the cost is decreasing as t increases, until the point 2/3 where it starts to increase.
See also
- Poisson processPoisson processA Poisson process, named after the French mathematician Siméon-Denis Poisson , is a stochastic process in which events occur continuously and independently of one another...
- Compound Poisson processCompound Poisson processA compound Poisson process is a continuous-time stochastic process with jumps. The jumps arrive randomly according to a Poisson process and the size of the jumps is also random, with a specified probability distribution...
- Continuous-time Markov process
- Semi-Markov processSemi-Markov processA continuous-time stochastic process is called a semi-Markov process or 'Markov renewal process' if the embedded jump chain is a Markov chain, and where the holding times are random variables with any distribution, whose distribution function may depend on the two states between which the move is...
- Queueing theoryQueueing theoryQueueing theory is the mathematical study of waiting lines, or queues. The theory enables mathematical analysis of several related processes, including arriving at the queue, waiting in the queue , and being served at the front of the queue...
- Ruin theoryRuin theoryRuin theory, sometimes referred to as collective risk theory, is a branch of actuarial science that studies an insurer's vulnerability to insolvency based on mathematical modeling of the insurer's surplus....
- Campbell's theoremCampbell's theoremCampbell's theorem, also known as Campbell’s embedding theorem and the Campbell-Magaarrd theorem, is a mathematical theorem that evaluates the asymptotic distribution of random impulses acting with a determined intensity on a damped system...
- Little's lemma








