
Infinite divisibility (probability)
Encyclopedia
The concepts of infinite divisibility and the decomposition of distributions arise in probability
and statistics
in relation to seeking families of probability distributions that might be a natural choice in certain applications, in the same way that the normal distribution is. The distributions sought correspond to random variables which are equivalent to the sums of a number of independent and identically distributed random variables
, where the number of such variables can be set to any pre-specified number.
The term infinitely divisible characteristic function is used for the characteristic function
of any infinitely divisible distribution.
The concept of infinite divisibility of probability distributions was introduced in 1929 by Bruno de Finetti
.
These distributions play a very important role in probability theory
in the context of limit theorems.
, to say that a probability distribution
F on the real line is infinitely divisible means that, for every positive integer n, there exist n independent
identically distributed random variables Xn1, ..., Xnn whose sum Sn = Xn1 + … + Xnn has the distribution F.
, the negative binomial distribution
, the Gamma distribution and the degenerate distribution are examples of infinitely divisible distributions; as are the normal distribution, Cauchy distribution
and all other members of the stable distribution family. The uniform distribution
and the binomial distribution are not infinitely divisible. The Student's t-distribution is infinitely divisible, while the distribution of the reciprocal of a random variable having a Student's t-distribution, is not.
: the limit as n → +∞ of the sum Sn = Xn1 + … Xnn of independent
uniformly asymptotically negligible (u.a.n.) random variables within a triangular array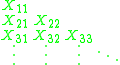
approaches — in the weak sense — an infinitely divisible distribution. The uniformly asymptotically negligible (u.a.n.) condition is given by
Thus, for example, if the uniform asymptotic negligibility (u.a.n.) condition is satisfied via an appropriate scaling of identically distributed random variables with finite variance
, the weak convergence is to the normal distribution in the classical version of the central limit theorem. More generally, if the u.a.n. condition is satisfied via a scaling of identically distributed random variables (with not necessarily finite second moment), then the weak convergence is to a stable distribution. On the other hand, for a triangular array
of independent (unscaled) Bernoulli random variables where the u.a.n. condition is satisfied through
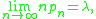
the weak convergence of the sum is to the Poisson distribution with mean λ as shown by the familiar proof of the law of small numbers.
. A Lévy process is a stochastic process
{ Lt : t ≥ 0 } with stationary independent increments, where stationary means that for s < t, the probability distribution
of Lt − Ls depends only on t − s and where independent increments means that that difference Lt − Ls is independent
of the corresponding difference on any interval not overlapping with [s, t], and similarly for any finite number of mutually non-overlapping intervals.
If { Lt : t ≥ 0 } is a Lévy process then, for any t ≥ 0, the random variable Lt will be infinitely divisible: for any n, we can choose (Xn0, Xn1, …, Xnn) = (Lt/n − L0, L2t/n − Lt/n, …, Lt − L(n-1)t/n). Similarly, Lt − Ls is infinitely divisible for any s < t.
On the other hand, if F is an infinitely divisible distribution, we can construct a Lévy process { Lt : t ≥ 0 } from it. For any interval [s, t] where t − s > 0 equals a rational number
p/q, we can define Lt − Ls to have the same distribution as Xq1 + Xq2 + … + Xqp. Irrational
values of t − s > 0 are handled via a continuity argument.
Probability
Probability is ordinarily used to describe an attitude of mind towards some proposition of whose truth we arenot certain. The proposition of interest is usually of the form "Will a specific event occur?" The attitude of mind is of the form "How certain are we that the event will occur?" The...
and statistics
Statistics
Statistics is the study of the collection, organization, analysis, and interpretation of data. It deals with all aspects of this, including the planning of data collection in terms of the design of surveys and experiments....
in relation to seeking families of probability distributions that might be a natural choice in certain applications, in the same way that the normal distribution is. The distributions sought correspond to random variables which are equivalent to the sums of a number of independent and identically distributed random variables
Independent and identically distributed random variables
In probability theory and statistics, a sequence or other collection of random variables is independent and identically distributed if each random variable has the same probability distribution as the others and all are mutually independent....
, where the number of such variables can be set to any pre-specified number.
The term infinitely divisible characteristic function is used for the characteristic function
Characteristic function (probability theory)
In probability theory and statistics, the characteristic function of any random variable completely defines its probability distribution. Thus it provides the basis of an alternative route to analytical results compared with working directly with probability density functions or cumulative...
of any infinitely divisible distribution.
The concept of infinite divisibility of probability distributions was introduced in 1929 by Bruno de Finetti
Bruno de Finetti
Bruno de Finetti was an Italian probabilist, statistician and actuary, noted for the "operational subjective" conception of probability...
.
These distributions play a very important role in probability theory
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
in the context of limit theorems.
Definition
In probability theoryProbability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
, to say that a probability distribution
Probability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
F on the real line is infinitely divisible means that, for every positive integer n, there exist n independent
Statistical independence
In probability theory, to say that two events are independent intuitively means that the occurrence of one event makes it neither more nor less probable that the other occurs...
identically distributed random variables Xn1, ..., Xnn whose sum Sn = Xn1 + … + Xnn has the distribution F.
Examples
The Poisson distributionPoisson distribution
In probability theory and statistics, the Poisson distribution is a discrete probability distribution that expresses the probability of a given number of events occurring in a fixed interval of time and/or space if these events occur with a known average rate and independently of the time since...
, the negative binomial distribution
Negative binomial distribution
In probability theory and statistics, the negative binomial distribution is a discrete probability distribution of the number of successes in a sequence of Bernoulli trials before a specified number of failures occur...
, the Gamma distribution and the degenerate distribution are examples of infinitely divisible distributions; as are the normal distribution, Cauchy distribution
Cauchy distribution
The Cauchy–Lorentz distribution, named after Augustin Cauchy and Hendrik Lorentz, is a continuous probability distribution. As a probability distribution, it is known as the Cauchy distribution, while among physicists, it is known as the Lorentz distribution, Lorentz function, or Breit–Wigner...
and all other members of the stable distribution family. The uniform distribution
Uniform distribution (continuous)
In probability theory and statistics, the continuous uniform distribution or rectangular distribution is a family of probability distributions such that for each member of the family, all intervals of the same length on the distribution's support are equally probable. The support is defined by...
and the binomial distribution are not infinitely divisible. The Student's t-distribution is infinitely divisible, while the distribution of the reciprocal of a random variable having a Student's t-distribution, is not.
Limit theorem
Infinitely divisible distributions appear in a broad generalization of the central limit theoremCentral limit theorem
In probability theory, the central limit theorem states conditions under which the mean of a sufficiently large number of independent random variables, each with finite mean and variance, will be approximately normally distributed. The central limit theorem has a number of variants. In its common...
: the limit as n → +∞ of the sum Sn = Xn1 + … Xnn of independent
Statistical independence
In probability theory, to say that two events are independent intuitively means that the occurrence of one event makes it neither more nor less probable that the other occurs...
uniformly asymptotically negligible (u.a.n.) random variables within a triangular array
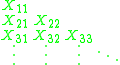
approaches — in the weak sense — an infinitely divisible distribution. The uniformly asymptotically negligible (u.a.n.) condition is given by
Thus, for example, if the uniform asymptotic negligibility (u.a.n.) condition is satisfied via an appropriate scaling of identically distributed random variables with finite variance
Variance
In probability theory and statistics, the variance is a measure of how far a set of numbers is spread out. It is one of several descriptors of a probability distribution, describing how far the numbers lie from the mean . In particular, the variance is one of the moments of a distribution...
, the weak convergence is to the normal distribution in the classical version of the central limit theorem. More generally, if the u.a.n. condition is satisfied via a scaling of identically distributed random variables (with not necessarily finite second moment), then the weak convergence is to a stable distribution. On the other hand, for a triangular array
Triangular array
In mathematics and computing, a triangular array of numbers, polynomials, or the like, is a doubly indexed sequence in which each row is only as long as the row's own index.Notable particular examples include these:...
of independent (unscaled) Bernoulli random variables where the u.a.n. condition is satisfied through
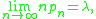
the weak convergence of the sum is to the Poisson distribution with mean λ as shown by the familiar proof of the law of small numbers.
Lévy process
Every infinitely divisible probability distribution corresponds in a natural way to a Lévy processLévy process
In probability theory, a Lévy process, named after the French mathematician Paul Lévy, is any continuous-time stochastic process that starts at 0, admits càdlàg modification and has "stationary independent increments" — this phrase will be explained below...
. A Lévy process is a stochastic process
Stochastic process
In probability theory, a stochastic process , or sometimes random process, is the counterpart to a deterministic process...
{ Lt : t ≥ 0 } with stationary independent increments, where stationary means that for s < t, the probability distribution
Probability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
of Lt − Ls depends only on t − s and where independent increments means that that difference Lt − Ls is independent
Statistical independence
In probability theory, to say that two events are independent intuitively means that the occurrence of one event makes it neither more nor less probable that the other occurs...
of the corresponding difference on any interval not overlapping with [s, t], and similarly for any finite number of mutually non-overlapping intervals.
If { Lt : t ≥ 0 } is a Lévy process then, for any t ≥ 0, the random variable Lt will be infinitely divisible: for any n, we can choose (Xn0, Xn1, …, Xnn) = (Lt/n − L0, L2t/n − Lt/n, …, Lt − L(n-1)t/n). Similarly, Lt − Ls is infinitely divisible for any s < t.
On the other hand, if F is an infinitely divisible distribution, we can construct a Lévy process { Lt : t ≥ 0 } from it. For any interval [s, t] where t − s > 0 equals a rational number
Rational number
In mathematics, a rational number is any number that can be expressed as the quotient or fraction a/b of two integers, with the denominator b not equal to zero. Since b may be equal to 1, every integer is a rational number...
p/q, we can define Lt − Ls to have the same distribution as Xq1 + Xq2 + … + Xqp. Irrational
Irrational number
In mathematics, an irrational number is any real number that cannot be expressed as a ratio a/b, where a and b are integers, with b non-zero, and is therefore not a rational number....
values of t − s > 0 are handled via a continuity argument.


