Compound Poisson distribution
Encyclopedia
In probability theory
, a compound Poisson distribution is the probability distribution
of the sum of a "Poisson-distributed number" of independent identically-distributed random variables. In the simplest cases, the result can be either a continuous or a discrete distribution.
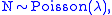
i.e., N is a random variable
whose distribution is a Poisson distribution
with expected value
λ, and that
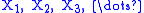
are identically distributed random variables that are mutually independent and also independent of N. Then the probability distribution of the sum of
i.i.d. random variables conditioned on the number of these variables (
):
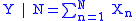
is a well-defined distribution. In the case N = 0, then the value of Y is 0, so that then Y | N=0 has a degenerate distribution.
The compound Poisson distribution is obtained by marginalising the joint distribution of (Y,N) over N, where this joint distribution is obtained by combining the conditional distribution Y | N with the marginal distribution of N.
and variance
of the compound distribution derive in a simple way from law of total expectation
and the law of total variance
. Thus
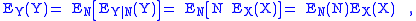
giving
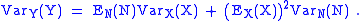
Then, since E(N)=Var(N) if N is Poisson, and dropping the unnecessary subscripts, these formulae can be reduced to
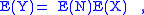
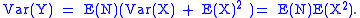
The probability distribution of Y can be determined in terms of characteristic function
s:
and hence, using the probability generating function of the Poisson distribution,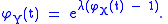
An alternative approach is via cumulant generating functions:
Via the law of total cumulance
it can be shown that, if the mean of the Poisson distribution λ=1, the cumulant
s of Y are the same as the moments
of X1.
It can be shown that every infinitely divisible
probability distribution is a limit of compound Poisson distributions.
or a gamma distribution, then the conditional distributions of Y | N are gamma distributions in which the shape parameters are proportional to N. This shows that the formulation of the "compound Poisson distribution" outlined above is essentially the same as the more general class of compound probability distribution
s. However, the properties outlined above do depend on its formulation as the sum of a Poisson-distributed number of random variables. The distribution of Y in the case of the compound Poisson distribution with exponentially-distributed summands can be written in an form.
with rate
and jump size distribution G is a continuous-time stochastic process
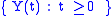given by
where the sum is by convention equal to zero as long as N(t)=0. Here,
is a Poisson process
with rate
, and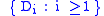 
are independent and identically distributed random variables, with distribution function G, which are also independent of 
, was used by Revfeim to model the distribution of the total rainfall in a day, where each day contains a Poisson-distributed number of events each of which provides an amount of rainfall which has an exponential distribution. Thompson applied the same model to monthly total rainfalls.
The compound Poisson distribution is also widely used in actuarial science
and insurance for modelling the distribution of the total claim amount
of the sum of a random number 
of independent and identically distributed claim amounts X1, X2, ... , XN.
Probability theory
Probability theory is the branch of mathematics concerned with analysis of random phenomena. The central objects of probability theory are random variables, stochastic processes, and events: mathematical abstractions of non-deterministic events or measured quantities that may either be single...
, a compound Poisson distribution is the probability distribution
Probability distribution
In probability theory, a probability mass, probability density, or probability distribution is a function that describes the probability of a random variable taking certain values....
of the sum of a "Poisson-distributed number" of independent identically-distributed random variables. In the simplest cases, the result can be either a continuous or a discrete distribution.
Definition
Suppose that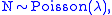i.e., N is a random variable
Random variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
whose distribution is a Poisson distribution
Poisson distribution
In probability theory and statistics, the Poisson distribution is a discrete probability distribution that expresses the probability of a given number of events occurring in a fixed interval of time and/or space if these events occur with a known average rate and independently of the time since...
with expected value
Expected value
In probability theory, the expected value of a random variable is the weighted average of all possible values that this random variable can take on...
λ, and that
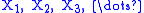
are identically distributed random variables that are mutually independent and also independent of N. Then the probability distribution of the sum of
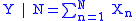
i.i.d. random variables conditioned on the number of these variables ():is a well-defined distribution. In the case N = 0, then the value of Y is 0, so that then Y | N=0 has a degenerate distribution.
The compound Poisson distribution is obtained by marginalising the joint distribution of (Y,N) over N, where this joint distribution is obtained by combining the conditional distribution Y | N with the marginal distribution of N.
Properties
MeanMean
In statistics, mean has two related meanings:* the arithmetic mean .* the expected value of a random variable, which is also called the population mean....
and variance
Variance
In probability theory and statistics, the variance is a measure of how far a set of numbers is spread out. It is one of several descriptors of a probability distribution, describing how far the numbers lie from the mean . In particular, the variance is one of the moments of a distribution...
of the compound distribution derive in a simple way from law of total expectation
Law of total expectation
The proposition in probability theory known as the law of total expectation, the law of iterated expectations, the tower rule, the smoothing theorem, among other names, states that if X is an integrable random variable The proposition in probability theory known as the law of total expectation, ...
and the law of total variance
Law of total variance
In probability theory, the law of total variance or variance decomposition formula states that if X and Y are random variables on the same probability space, and the variance of Y is finite, then...
. Thus
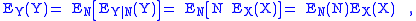
giving
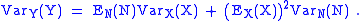
Then, since E(N)=Var(N) if N is Poisson, and dropping the unnecessary subscripts, these formulae can be reduced to
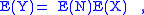
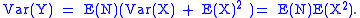
The probability distribution of Y can be determined in terms of characteristic function
Characteristic function (probability theory)
In probability theory and statistics, the characteristic function of any random variable completely defines its probability distribution. Thus it provides the basis of an alternative route to analytical results compared with working directly with probability density functions or cumulative...
s:
and hence, using the probability generating function of the Poisson distribution,
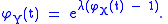
An alternative approach is via cumulant generating functions:
Via the law of total cumulance
Law of total cumulance
In probability theory and mathematical statistics, the law of total cumulance is a generalization to cumulants of the law of total probability, the law of total expectation, and the law of total variance. It has applications in the analysis of time series...
it can be shown that, if the mean of the Poisson distribution λ=1, the cumulant
Cumulant
In probability theory and statistics, the cumulants κn of a probability distribution are a set of quantities that provide an alternative to the moments of the distribution. The moments determine the cumulants in the sense that any two probability distributions whose moments are identical will have...
s of Y are the same as the moments
Moment (mathematics)
In mathematics, a moment is, loosely speaking, a quantitative measure of the shape of a set of points. The "second moment", for example, is widely used and measures the "width" of a set of points in one dimension or in higher dimensions measures the shape of a cloud of points as it could be fit by...
of X1.
It can be shown that every infinitely divisible
Infinite divisibility
The concept of infinite divisibility arises in different ways in philosophy, physics, economics, order theory , and probability theory...
probability distribution is a limit of compound Poisson distributions.
Special cases
If the distribution of X is either an exponential distributionExponential distribution
In probability theory and statistics, the exponential distribution is a family of continuous probability distributions. It describes the time between events in a Poisson process, i.e...
or a gamma distribution, then the conditional distributions of Y | N are gamma distributions in which the shape parameters are proportional to N. This shows that the formulation of the "compound Poisson distribution" outlined above is essentially the same as the more general class of compound probability distribution
Compound probability distribution
In probability theory, a compound probability distribution is the probability distribution that results from assuming that a random variable is distributed according to some parametrized distribution F with an unknown parameter θ that is distributed according to some other distribution G, and then...
s. However, the properties outlined above do depend on its formulation as the sum of a Poisson-distributed number of random variables. The distribution of Y in the case of the compound Poisson distribution with exponentially-distributed summands can be written in an form.
Compound Poisson processes
A compound Poisson processCompound Poisson process
A compound Poisson process is a continuous-time stochastic process with jumps. The jumps arrive randomly according to a Poisson process and the size of the jumps is also random, with a specified probability distribution...
with rate
and jump size distribution G is a continuous-time stochastic processStochastic process
In probability theory, a stochastic process , or sometimes random process, is the counterpart to a deterministic process...
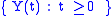given bywhere the sum is by convention equal to zero as long as N(t)=0. Here,
is a Poisson processPoisson process
A Poisson process, named after the French mathematician Siméon-Denis Poisson , is a stochastic process in which events occur continuously and independently of one another...
with rate
, and are independent and identically distributed random variables, with distribution function G, which are also independent of Applications
A compound Poisson distribution, in which the summands have an exponential distributionExponential distribution
In probability theory and statistics, the exponential distribution is a family of continuous probability distributions. It describes the time between events in a Poisson process, i.e...
, was used by Revfeim to model the distribution of the total rainfall in a day, where each day contains a Poisson-distributed number of events each of which provides an amount of rainfall which has an exponential distribution. Thompson applied the same model to monthly total rainfalls.
The compound Poisson distribution is also widely used in actuarial science
Actuarial science
Actuarial science is the discipline that applies mathematical and statistical methods to assess risk in the insurance and finance industries. Actuaries are professionals who are qualified in this field through education and experience...
and insurance for modelling the distribution of the total claim amount
of the sum of a random number of independent and identically distributed claim amounts X1, X2, ... , XN.