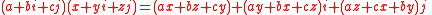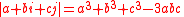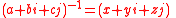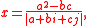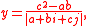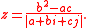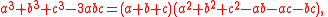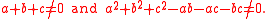Tricomplex number
Encyclopedia
In mathematics
, the tricomplex numbers are a three-dimensional hypercomplex number
system developed by Silviu Olariu in his book Complex Numbers in n Dimensions (2002).
, were 
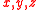are three real numbers and 
are two imaginary units with the following properties 
, 
and 
. Tricomplex numbers form an abelian group.
Addition/subtraction:
Multiplication:
Modulus:
Inverse:
with
From the fact that
it follows that
has an inverse if and only if
s if and only if they lie on neither the trisector line nor the nodal plane.
"It can be shown that if uu′ = 0 then either u = 0, or u′ = 0, or one of the tricomplex numbers u, u′ belongs to the trisector line (t) and the other belongs to the nodal plane."
Interpreted as a linear operator on space
, tricomplex number x + y i + z j represents the linear combination of three operators: x which re-scales the R and r parameters, i which changes θ to θ + 120°, and j which changes it to θ + 240°.
.
Note that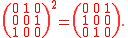
Furthermore, the product of these two matrices is the identity matrix
. One can take either one of these matrices to represent i (say the first), and the other to represent j.
Then the tricomplex number x + y i + z j is represented by the matrix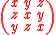
which lies in the 9-dimensional ring
of 3 x 3 real matrices.
The algebra of tricomplex numbers corresponds to a commutative 3-dimensional subalgebra
.
The determinant
m of the matrix is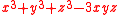
. Since a matrix has an inverse only when the determinant is non-zero, this polynomial is taken as the modulus of the tricomplex number.
applied to the axis {ai : a ∈ R} which results in a transcendental curve
: {exp(ai) : a ∈ R} where
Olariu calls these three infinite series in a the cosexponential functions for the tricomplex numbers. His notation for the three series is cx(a), mx(a), and px(a). Evidently exp(ai) = cx(a) + i mx(a) + j px(a). Differentiating the curve with respect to the parameter a, one finds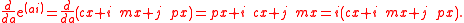
Thus at any point of the curve exp(ai), the tangent vector to the curve is given by i exp(ai).
Any of the cosexponential functions is a solution to the differential equation
y(3) = y.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the tricomplex numbers are a three-dimensional hypercomplex number
Hypercomplex number
In mathematics, a hypercomplex number is a traditional term for an element of an algebra over a field where the field is the real numbers or the complex numbers. In the nineteenth century number systems called quaternions, tessarines, coquaternions, biquaternions, and octonions became established...
system developed by Silviu Olariu in his book Complex Numbers in n Dimensions (2002).
Definition
A tricomplex number is defined to be the 3-tuple, were 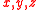are three real numbers and are two imaginary units with the following properties , and . Tricomplex numbers form an abelian group.Addition/subtraction:
Multiplication:
Modulus:
Inverse:
with
From the fact that
it follows that
has an inverse if and only if
Trisector line and nodal plane
The geometry of tricomplex numbers is described in terms of the trisector line (t) where all three coordinates are equal, and the nodal plane Π which passes through the origin and is perpendicular to the trisector line. These are important because tricomplex numbers have multiplicative inverseMultiplicative inverse
In mathematics, a multiplicative inverse or reciprocal for a number x, denoted by 1/x or x−1, is a number which when multiplied by x yields the multiplicative identity, 1. The multiplicative inverse of a fraction a/b is b/a. For the multiplicative inverse of a real number, divide 1 by the...
s if and only if they lie on neither the trisector line nor the nodal plane.
"It can be shown that if uu′ = 0 then either u = 0, or u′ = 0, or one of the tricomplex numbers u, u′ belongs to the trisector line (t) and the other belongs to the nodal plane."
Alternate parametrization
The set {1, i, j} is permuted by multiplication with i. Such a permutation occurs when the plane S = {x + y i + z j : x + y + z = 1} is rotated by 120°. The center is (1 + i + j)/√3. The line from the origin through this center forms a axis for a cylindrical coordinate system (R, r, θ) as follows: any tricomplex number lies on a plane parallel to S at a distance R from the origin, with (r, θ) corresponding to polar coordinates of the tricomplex number in its plane parallel to S. An auxiliary coordinate φ can be used to express the angle between the axis and the ray to the tricomplex number.Interpreted as a linear operator on space
Space
Space is the boundless, three-dimensional extent in which objects and events occur and have relative position and direction. Physical space is often conceived in three linear dimensions, although modern physicists usually consider it, with time, to be part of a boundless four-dimensional continuum...
, tricomplex number x + y i + z j represents the linear combination of three operators: x which re-scales the R and r parameters, i which changes θ to θ + 120°, and j which changes it to θ + 240°.
Presentation as subalgebra
Tricomplex numbers can be associated with a space of matricesMatrix (mathematics)
In mathematics, a matrix is a rectangular array of numbers, symbols, or expressions. The individual items in a matrix are called its elements or entries. An example of a matrix with six elements isMatrices of the same size can be added or subtracted element by element...
.
Note that
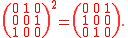
Furthermore, the product of these two matrices is the identity matrix
Identity matrix
In linear algebra, the identity matrix or unit matrix of size n is the n×n square matrix with ones on the main diagonal and zeros elsewhere. It is denoted by In, or simply by I if the size is immaterial or can be trivially determined by the context...
. One can take either one of these matrices to represent i (say the first), and the other to represent j.
Then the tricomplex number x + y i + z j is represented by the matrix
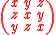
which lies in the 9-dimensional ring
Ring (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
of 3 x 3 real matrices.
The algebra of tricomplex numbers corresponds to a commutative 3-dimensional subalgebra
Subalgebra
In mathematics, the word "algebra", when referring to a structure, often means a vector space or module equipped with an additional bilinear operation. Algebras in universal algebra are far more general: they are a common generalisation of all algebraic structures...
.
The determinant
Determinant
In linear algebra, the determinant is a value associated with a square matrix. It can be computed from the entries of the matrix by a specific arithmetic expression, while other ways to determine its value exist as well...
m of the matrix is
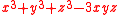. Since a matrix has an inverse only when the determinant is non-zero, this polynomial is taken as the modulus of the tricomplex number.Cosexponential functions
The basic tricomplex number i satisfies i3 = 1, so the general in depends only on the residue class of n modulo 3, and in is in {1, i, j} since i2 = j. Now consider the exponential mapExponential map
In differential geometry, the exponential map is a generalization of the ordinary exponential function of mathematical analysis to all differentiable manifolds with an affine connection....
applied to the axis {ai : a ∈ R} which results in a transcendental curve
Transcendental curve
In mathematics, a transcendental curve is a curve that is not an algebraic curve. Here for a curve C what matters is the point set underlying C, not a given parametrisation...
: {exp(ai) : a ∈ R} where
Olariu calls these three infinite series in a the cosexponential functions for the tricomplex numbers. His notation for the three series is cx(a), mx(a), and px(a). Evidently exp(ai) = cx(a) + i mx(a) + j px(a). Differentiating the curve with respect to the parameter a, one finds
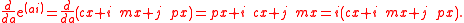
Thus at any point of the curve exp(ai), the tangent vector to the curve is given by i exp(ai).
Any of the cosexponential functions is a solution to the differential equation
Differential equation
A differential equation is a mathematical equation for an unknown function of one or several variables that relates the values of the function itself and its derivatives of various orders...
y(3) = y.