
Sedenion
Overview
Abstract algebra
Abstract algebra is the subject area of mathematics that studies algebraic structures, such as groups, rings, fields, modules, vector spaces, and algebras...
, sedenions form a 16-dimensional non-associative algebra
Algebra over a field
In mathematics, an algebra over a field is a vector space equipped with a bilinear vector product. That is to say, it isan algebraic structure consisting of a vector space together with an operation, usually called multiplication, that combines any two vectors to form a third vector; to qualify as...
over the reals
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
obtained by applying the Cayley–Dickson construction to the octonions. The set of sedenions is denoted by
 .
.The term "sedenion" is also used for other 16-dimensional algebraic structures, such as a tensor product of 2 copies of the quaternions, or the algebra of 4 by 4 matrices over the reals, or that studied by .
Like (Cayley–Dickson) octonion
Octonion
In mathematics, the octonions are a normed division algebra over the real numbers, usually represented by the capital letter O, using boldface O or blackboard bold \mathbb O. There are only four such algebras, the other three being the real numbers R, the complex numbers C, and the quaternions H...
s, multiplication
Multiplication
Multiplication is the mathematical operation of scaling one number by another. It is one of the four basic operations in elementary arithmetic ....
of Cayley–Dickson sedenions is neither commutative nor associative.
But in contrast to the octonions, the sedenions do not even have the property of being alternative
Alternative algebra
In abstract algebra, an alternative algebra is an algebra in which multiplication need not be associative, only alternative. That is, one must have*x = y*x = y...
.
They do, however, have the property of power associativity
Power associativity
In abstract algebra, power associativity is a property of a binary operation which is a weak form of associativity.An algebra is said to be power-associative if the subalgebra generated by any element is associative....
, which can be stated as for any element x of
 , the power
, the power 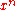 is well-defined.
is well-defined.Every sedenion is a real linear combination
Linear combination
In mathematics, a linear combination is an expression constructed from a set of terms by multiplying each term by a constant and adding the results...
of the unit sedenions 1, e1, e2, e3, ..., and e15,
which form a basis of the vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
of sedenions.
The sedenions have a multiplicative identity element
Identity element
In mathematics, an identity element is a special type of element of a set with respect to a binary operation on that set. It leaves other elements unchanged when combined with them...
1 and multiplicative inverses, but they are not a division algebra
Division algebra
In the field of mathematics called abstract algebra, a division algebra is, roughly speaking, an algebra over a field, in which division is possible.- Definitions :...
.
Discussions

