Homomorphic encryption
Encyclopedia
Homomorphic encryption is a form of encryption
where a specific algebraic operation performed on the plaintext
is equivalent to another (possibly different) algebraic operation performed on the ciphertext
. Depending on one's viewpoint, this can be seen as either a positive or negative attribute of the cryptosystem. Homomorphic encryption schemes are malleable
by design. The homomorphic property of various cryptosystems can be used to create secure voting systems, collision-resistant hash functions, private information retrieval
schemes and enable widespread use of cloud computing by ensuring the confidentiality of processed data.
There are several efficient, partially homomorphic cryptosystems, and two fully homomorphic, but less efficient cryptosystems.
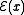is used to denote the encryption of the message x.
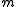and exponent 
, then the encryption of a message 
is given by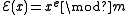 
. The homomorphic property is then
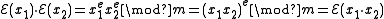
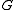, if the public key is 
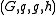, where 
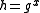, and 
is the secret key, then the encryption of a message 
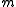is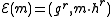 
, for some 
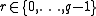. The homomorphic property is then
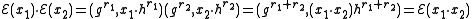
, if the public key is the modulus m and quadratic non-residue x, then the encryption of a bit b is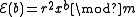
. The homomorphic property is then
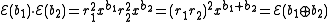
where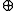
denotes addition modulo 2, (i.e. exclusive-or
).
, if the public key is the modulus m and the base g with a blocksize of r, then the encryption of a message x is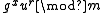
. The homomorphic property is then
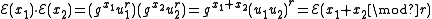
, if the public key is the modulus m and the base g, then the encryption of a message x is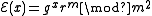
. The homomorphic property is then
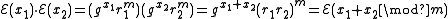
structure of the plaintexts) is known as fully homomorphic encryption (FHE) and is far more powerful. Using such a scheme, any circuit can be homomorphically evaluated, effectively allowing the construction of programs which may be run on encryptions of their inputs to produce an encryption of their output. Since such a program never decrypts its input, it can be run by an untrusted party without revealing its inputs and internal state. The existence of an efficient and fully homomorphic cryptosystem would have great practical implications in the outsourcing of private computations, for instance, in the context of cloud computing
.
The "homomorphic" part of a fully homomorphic encryption scheme can also be described in terms of category theory
. If C is the category
whose objects are integers (i.e., finite streams of data) and whose morphisms are computable functions
, then (ideally) a fully homomorphic encryption scheme elevates an encryption function to a functor
from C to itself.
The utility of fully homomorphic encryption has been long recognized. The problem of constructing such a scheme was first proposed within a year of the development of RSA. A solution proved more elusive; for more than 30 years, it was unclear whether fully homomorphic encryption was even possible. During this period, the best result was the Boneh-Goh-Nissim cryptosystem which supports evaluation of an unlimited number of addition operations but at most one multiplication.
Craig Gentry using lattice-based cryptography showed the first fully homomorphic encryption scheme as announced by IBM on June 25, 2009. His scheme supports evaluations of arbitrary depth circuits.
His construction starts from a somewhat homomorphic encryption scheme using ideal lattices
that is limited to evaluating low-degree polynomials over encrypted data. (It is limited because each ciphertext is noisy in some sense, and this noise grows as one adds and multiplies ciphertexts, until ultimately the noise makes the resulting ciphertext indecipherable.) He then shows how to modify this scheme to make it bootstrappable—in particular, he shows that by modifying the somewhat homomorphic scheme slightly, it can actually evaluate its own decryption circuit, a self-referential property. Finally, he shows that any bootstrappable somewhat homomorphic encryption scheme can be converted into a fully homomorphic encryption through a recursive self-embedding. In the particular case of Gentry's ideal-lattice-based somewhat homomorphic scheme, this bootstrapping procedure effectively "refreshes" the ciphertext by reducing its associated noise so that it can be used thereafter in more additions and multiplications without resulting in an indecipherable ciphertext. Gentry based the security of his scheme on the assumed hardness of two problems: certain worst-case problems over ideal lattices
, and the sparse (or low-weight) subset sum problem.
Regarding performance, ciphertexts in Gentry's scheme remain compact insofar as their lengths do not depend at all on the complexity of the function that is evaluated over the encrypted data. The computational time only depends linearly on the number of operations performed. However, the scheme is impractical for many applications, because ciphertext size and computation time increase sharply as one increases the security level. To obtain 2k security against known attacks, the computation time and ciphertext size are high-degree polynomials in k. Recently, Stehle and Steinfeld reduced the dependence on k substantially.
They presented optimizations that permit the computation to be only quasi-k3.5 per boolean gate of the function being evaluated.
Gentry's Ph.D. thesis
provides additional details.
Gentry also published a high-level overview of the van Dijk et al. construction (described below) in the March 2010 issue of Communications of the ACM.
In 2009, Marten van Dijk, Craig Gentry, Shai Halevi and Vinod Vaikuntanathan presented a second fully homomorphic encryption scheme,
which uses many of the tools of Gentry's construction, but which does not require ideal lattices
. Instead, they show that the somewhat homomorphic component of Gentry's ideal lattice
-based scheme can be replaced with a very simple somewhat homomorphic scheme that uses integers. The scheme is therefore conceptually simpler than Gentry's ideal lattice scheme, but has similar properties with regards to homomorphic operations and efficiency. The somewhat homomorphic component in the work of van Dijk et al. is similar to an encryption scheme proposed by Levieil and Naccache in 2008, and also to one that was proposed by Bram Cohen in 1998.
Cohen's method is not even additively homomorphic, however. The Levieil-Naccache scheme is additively homomorphic, and can be modified to support also a small number of multiplications.
In 2010, Nigel P. Smart
and Frederik Vercauteren presented a refinement of Gentry's scheme giving smaller key and ciphertext sizes, but which is still not fully practical. At the rump session of Eurocrypt 2010, Craig Gentry and Shai Halevi presented a working implementation of fully homomorphic encryption (i.e. the entire bootstrapping procedure) together with performance numbers.
In 2010 Riggio and Sicari presented a practical application of homomorphic encryption to an hybrid wireless sensor/mesh network. The system enables transparent multi-hop wireless backhauls that are able to perform statistical analysis of different kinds of data (temperature, humidity, etc.) coming from a WSN while ensuring both end–to–end encryption and hop–by–hop authentication.
Recently, Coron, Naccache and Tibouchi proposed a technique allowing to reduce the public-key size of several FHE schemes below 1MB (4.6MB if provable security is desired).
Encryption
In cryptography, encryption is the process of transforming information using an algorithm to make it unreadable to anyone except those possessing special knowledge, usually referred to as a key. The result of the process is encrypted information...
where a specific algebraic operation performed on the plaintext
Plaintext
In cryptography, plaintext is information a sender wishes to transmit to a receiver. Cleartext is often used as a synonym. Before the computer era, plaintext most commonly meant message text in the language of the communicating parties....
is equivalent to another (possibly different) algebraic operation performed on the ciphertext
Ciphertext
In cryptography, ciphertext is the result of encryption performed on plaintext using an algorithm, called a cipher. Ciphertext is also known as encrypted or encoded information because it contains a form of the original plaintext that is unreadable by a human or computer without the proper cipher...
. Depending on one's viewpoint, this can be seen as either a positive or negative attribute of the cryptosystem. Homomorphic encryption schemes are malleable
Malleability (cryptography)
Malleability is a property of some cryptographic algorithms. An encryption algorithm is malleable if it is possible for an adversary to transform a ciphertext into another ciphertext which decrypts to a related plaintext...
by design. The homomorphic property of various cryptosystems can be used to create secure voting systems, collision-resistant hash functions, private information retrieval
Private information retrieval
In cryptography, a private information retrieval protocol allows a user to retrieve an item from a server in possession of a database without revealing which item they are retrieving...
schemes and enable widespread use of cloud computing by ensuring the confidentiality of processed data.
There are several efficient, partially homomorphic cryptosystems, and two fully homomorphic, but less efficient cryptosystems.
Partially homomorphic cryptosystems
In the following examples, the notation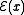 is used to denote the encryption of the message x.Unpadded RSA
If the RSA public key is modulus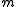 and exponent , then the encryption of a message is given by 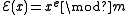. The homomorphic property is then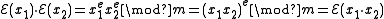ElGamal
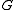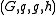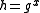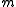In the ElGamal cryptosystem, in a group, if the public key is , where , and is the secret key, then the encryption of a message is 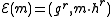, for some 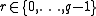. The homomorphic property is then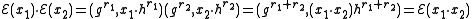Goldwasser-Micali
In the Goldwasser-Micali cryptosystemGoldwasser-Micali cryptosystem
The Goldwasser–Micali cryptosystem is an asymmetric key encryption algorithm developed by Shafi Goldwasser and Silvio Micali in 1982. GM has the distinction of being the first probabilistic public-key encryption scheme which is provably secure under standard cryptographic assumptions...
, if the public key is the modulus m and quadratic non-residue x, then the encryption of a bit b is
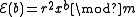. The homomorphic property is then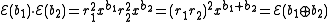where
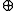denotes addition modulo 2, (i.e. exclusive-orExclusive disjunction
The logical operation exclusive disjunction, also called exclusive or , is a type of logical disjunction on two operands that results in a value of true if exactly one of the operands has a value of true...
).
Benaloh
In the Benaloh cryptosystemBenaloh cryptosystem
The Benaloh Cryptosystem is an extension of the Goldwasser-Micali cryptosystem created in 1994 by Josh Benaloh. The main improvement of the Benaloh Cryptosystem over GM is that longer blocks of data can be encrypted at once, whereas in GM each bit is encrypted individually.-Scheme...
, if the public key is the modulus m and the base g with a blocksize of r, then the encryption of a message x is
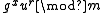. The homomorphic property is then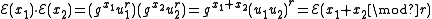Paillier
In the Paillier cryptosystemPaillier cryptosystem
The Paillier cryptosystem, named after and invented by Pascal Paillier in 1999, is a probabilistic asymmetric algorithm for public key cryptography. The problem of computing n-th residue classes is believed to be computationally difficult...
, if the public key is the modulus m and the base g, then the encryption of a message x is
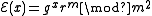. The homomorphic property is then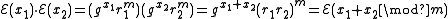Other partially homomorphic cryptosystems
- Okamoto–Uchiyama cryptosystem
- Naccache–Stern cryptosystem
- Damgård–Jurik cryptosystem
- Boneh–Goh–Nissim cryptosystem
Fully homomorphic encryption
Each of the examples listed above allows homomorphic computation of only one operation (either addition or multiplication) on plaintexts. A cryptosystem which supports both addition and multiplication (thereby preserving the ringRing (mathematics)
In mathematics, a ring is an algebraic structure consisting of a set together with two binary operations usually called addition and multiplication, where the set is an abelian group under addition and a semigroup under multiplication such that multiplication distributes over addition...
structure of the plaintexts) is known as fully homomorphic encryption (FHE) and is far more powerful. Using such a scheme, any circuit can be homomorphically evaluated, effectively allowing the construction of programs which may be run on encryptions of their inputs to produce an encryption of their output. Since such a program never decrypts its input, it can be run by an untrusted party without revealing its inputs and internal state. The existence of an efficient and fully homomorphic cryptosystem would have great practical implications in the outsourcing of private computations, for instance, in the context of cloud computing
Cloud computing
Cloud computing is the delivery of computing as a service rather than a product, whereby shared resources, software, and information are provided to computers and other devices as a utility over a network ....
.
The "homomorphic" part of a fully homomorphic encryption scheme can also be described in terms of category theory
Category theory
Category theory is an area of study in mathematics that examines in an abstract way the properties of particular mathematical concepts, by formalising them as collections of objects and arrows , where these collections satisfy certain basic conditions...
. If C is the category
Category (mathematics)
In mathematics, a category is an algebraic structure that comprises "objects" that are linked by "arrows". A category has two basic properties: the ability to compose the arrows associatively and the existence of an identity arrow for each object. A simple example is the category of sets, whose...
whose objects are integers (i.e., finite streams of data) and whose morphisms are computable functions
Computable function
Computable functions are the basic objects of study in computability theory. Computable functions are the formalized analogue of the intuitive notion of algorithm. They are used to discuss computability without referring to any concrete model of computation such as Turing machines or register...
, then (ideally) a fully homomorphic encryption scheme elevates an encryption function to a functor
Functor
In category theory, a branch of mathematics, a functor is a special type of mapping between categories. Functors can be thought of as homomorphisms between categories, or morphisms when in the category of small categories....
from C to itself.
The utility of fully homomorphic encryption has been long recognized. The problem of constructing such a scheme was first proposed within a year of the development of RSA. A solution proved more elusive; for more than 30 years, it was unclear whether fully homomorphic encryption was even possible. During this period, the best result was the Boneh-Goh-Nissim cryptosystem which supports evaluation of an unlimited number of addition operations but at most one multiplication.
Craig Gentry using lattice-based cryptography showed the first fully homomorphic encryption scheme as announced by IBM on June 25, 2009. His scheme supports evaluations of arbitrary depth circuits.
His construction starts from a somewhat homomorphic encryption scheme using ideal lattices
Ideal lattice cryptography
Ideal lattices are a special class of lattices and a generalization of cyclic lattices. Ideal lattices naturally occur in many parts of number theory, but also in other areas. In particular, they have a significant place in cryptography. Micciancio defined a generalization of cyclic lattices as...
that is limited to evaluating low-degree polynomials over encrypted data. (It is limited because each ciphertext is noisy in some sense, and this noise grows as one adds and multiplies ciphertexts, until ultimately the noise makes the resulting ciphertext indecipherable.) He then shows how to modify this scheme to make it bootstrappable—in particular, he shows that by modifying the somewhat homomorphic scheme slightly, it can actually evaluate its own decryption circuit, a self-referential property. Finally, he shows that any bootstrappable somewhat homomorphic encryption scheme can be converted into a fully homomorphic encryption through a recursive self-embedding. In the particular case of Gentry's ideal-lattice-based somewhat homomorphic scheme, this bootstrapping procedure effectively "refreshes" the ciphertext by reducing its associated noise so that it can be used thereafter in more additions and multiplications without resulting in an indecipherable ciphertext. Gentry based the security of his scheme on the assumed hardness of two problems: certain worst-case problems over ideal lattices
Ideal lattice cryptography
Ideal lattices are a special class of lattices and a generalization of cyclic lattices. Ideal lattices naturally occur in many parts of number theory, but also in other areas. In particular, they have a significant place in cryptography. Micciancio defined a generalization of cyclic lattices as...
, and the sparse (or low-weight) subset sum problem.
Regarding performance, ciphertexts in Gentry's scheme remain compact insofar as their lengths do not depend at all on the complexity of the function that is evaluated over the encrypted data. The computational time only depends linearly on the number of operations performed. However, the scheme is impractical for many applications, because ciphertext size and computation time increase sharply as one increases the security level. To obtain 2k security against known attacks, the computation time and ciphertext size are high-degree polynomials in k. Recently, Stehle and Steinfeld reduced the dependence on k substantially.
They presented optimizations that permit the computation to be only quasi-k3.5 per boolean gate of the function being evaluated.
Gentry's Ph.D. thesis
provides additional details.
Gentry also published a high-level overview of the van Dijk et al. construction (described below) in the March 2010 issue of Communications of the ACM.
In 2009, Marten van Dijk, Craig Gentry, Shai Halevi and Vinod Vaikuntanathan presented a second fully homomorphic encryption scheme,
which uses many of the tools of Gentry's construction, but which does not require ideal lattices
Ideal lattice cryptography
Ideal lattices are a special class of lattices and a generalization of cyclic lattices. Ideal lattices naturally occur in many parts of number theory, but also in other areas. In particular, they have a significant place in cryptography. Micciancio defined a generalization of cyclic lattices as...
. Instead, they show that the somewhat homomorphic component of Gentry's ideal lattice
Ideal lattice cryptography
Ideal lattices are a special class of lattices and a generalization of cyclic lattices. Ideal lattices naturally occur in many parts of number theory, but also in other areas. In particular, they have a significant place in cryptography. Micciancio defined a generalization of cyclic lattices as...
-based scheme can be replaced with a very simple somewhat homomorphic scheme that uses integers. The scheme is therefore conceptually simpler than Gentry's ideal lattice scheme, but has similar properties with regards to homomorphic operations and efficiency. The somewhat homomorphic component in the work of van Dijk et al. is similar to an encryption scheme proposed by Levieil and Naccache in 2008, and also to one that was proposed by Bram Cohen in 1998.
Cohen's method is not even additively homomorphic, however. The Levieil-Naccache scheme is additively homomorphic, and can be modified to support also a small number of multiplications.
In 2010, Nigel P. Smart
Nigel Smart (Cryptographer)
Nigel Smart is a professor in the Department of Computer Science at the University of Bristol and a current holder of the Royal Society-Wolfson Research Merit Award.He is best known for his work in Elliptic curve cryptography, especially work on the ECDLP...
and Frederik Vercauteren presented a refinement of Gentry's scheme giving smaller key and ciphertext sizes, but which is still not fully practical. At the rump session of Eurocrypt 2010, Craig Gentry and Shai Halevi presented a working implementation of fully homomorphic encryption (i.e. the entire bootstrapping procedure) together with performance numbers.
In 2010 Riggio and Sicari presented a practical application of homomorphic encryption to an hybrid wireless sensor/mesh network. The system enables transparent multi-hop wireless backhauls that are able to perform statistical analysis of different kinds of data (temperature, humidity, etc.) coming from a WSN while ensuring both end–to–end encryption and hop–by–hop authentication.
Recently, Coron, Naccache and Tibouchi proposed a technique allowing to reduce the public-key size of several FHE schemes below 1MB (4.6MB if provable security is desired).
See Also
- Homomorphic Signatures for Network CodingHomomorphic signatures for network codingNetwork coding has been shown to optimally use bandwidth in a network, maximizing information flow but the scheme is very inherently vulnerable to pollution attacks by malicious nodes in the network. A node injecting garbage can quickly affect many receivers...
- Verifiable computing using a fully homomorphic schemeVerifiable computingVerifiable computing is enabling a computer to offload the computation of some function, to other perhaps untrusted clients, while maintaining verifiable results. The other clients evaluate the function and return the result with a proof that the computation of the function was carried out correctly...