Sheaf cohomology
Encyclopedia
In mathematics
, sheaf cohomology is the aspect of sheaf theory, concerned with sheaves of abelian group
s, that applies homological algebra
to make possible effective calculation of the global sections of a sheaf F. This is the main step, in numerous areas, from sheaf theory as a description of a geometric problem, to its use as a tool capable of calculating dimensions of important geometric invariants.
Its development was rapid in the years after 1950, when it was realised that sheaf cohomology was connected with more classical methods applied to the Riemann-Roch theorem, the analysis of a linear system of divisors
in algebraic geometry
, several complex variables
, and Hodge theory
. The dimensions or ranks of sheaf cohomology groups became a fresh source of geometric data, or gave rise to new interpretations of older work.
, in which the relatively small change was made of attributing to an open set
U of a topological space
X an abelian group F(U) that 'varies' with U, rather than an abelian group A that is fixed ahead of time. This means that cochains are easy to write down rather concretely; in fact the model applications, such as the Cousin problems
on meromorphic function
s, stay within fairly familiar mathematical territory. From the sheaf point of view, the Čech theory is the restriction to the theory of sheaves of locally constant function
s with values in A. Within sheaf theory it is easy to see that 'twisted' versions, with local coefficients
on which the fundamental group
acts, are also subsumed — along with some very different sorts of more general coefficients.
One problem with that theory was that Čech cohomology itself fails to have good properties, unless X itself is well-behaved
. This is not a difficulty in case X is something like a manifold
; but embarrassing for applications to algebraic geometry, since the Zariski topology
is in general not Hausdorff
. The problem with the Čech theory manifests itself in the failure of the long exact sequence of cohomology groups associated to a short exact sequence of sheaves. This in practice is the basic method of attacking a calculation (i.e. to show how a given sheaf is involved with others in a short exact sequence, and draw consequences). The theory stood in this state of disarray only for a short while: Jean-Pierre Serre
showed that the Čech theory worked, and on the other hand Alexandre Grothendieck proposed a more abstract definition that would build in the long exact sequence.
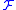as the right derived functor
of the global section
functor: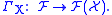
This functor is not an exact functor
, a fact familiar in other terms from the theory of branch cuts (for example, in the case of the logarithm
of a complex number
: see exponential sequence). It is a left exact functor, and therefore has a sequence of right derived functor
s, denoted by
The existence
of these derived functors is supplied by homological algebra
of the abelian category
of sheaves (and indeed this was a main reason to set up that theory). It depends on having injective resolutions; that is, in theory calculations can be done with injective resolutions, though in practice short and long exact sequences may be a better idea.
Because the derived functor can be computed by applying the functor to any acyclic resolution and keeping the cohomology of the complex, there are a number of other ways to compute cohomology groups. Depending on the concrete situation, fine, flasque, soft or acyclic sheaves are used to calculate concrete cohomology groups -- see injective sheaves
.
in the form of Borel-Moore homology
for locally compact space
s; to representation theory
in the Borel-Bott-Weil theorem; as well as becoming standard in algebraic geometry and complex manifold
s.
The particular needs of étale cohomology
were more about reinterpreting sheaf in sheaf cohomology, than cohomology, given that the derived functor approach applied. Flat cohomology, crystalline cohomology
and successors are also applications of the basic model.
of a sheaf 
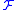is defined by
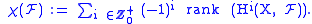
To make sense of this expression, which generalises the Euler characteristic
as alternating sum of Betti number
s, two conditions must be fulfilled. Firstly the summands must be almost all
zero, i.e. zero for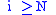
for some 
. Further, rank must be some well-defined function from module theory, such as rank of an abelian group
or vector space dimension, that yields finite values on the cohomology groups in question. Therefore finiteness theorems of two kinds are required.
In theories such as coherent cohomology, where such theorems exist, the value of χ(F) is typically easier to compute, from other considerations (for example the Hirzebruch-Riemann-Roch theorem
or Grothendieck-Riemann-Roch theorem), than the individual ranks separately. In practice it is often H0(X,F) that is of most interest; one way to compute its rank is then by means of a vanishing theorem
on the other Hi(X,F). This is a standard indirect method of sheaf theory to produce numerical results.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, sheaf cohomology is the aspect of sheaf theory, concerned with sheaves of abelian group
Abelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
s, that applies homological algebra
Homological algebra
Homological algebra is the branch of mathematics which studies homology in a general algebraic setting. It is a relatively young discipline, whose origins can be traced to investigations in combinatorial topology and abstract algebra at the end of the 19th century, chiefly by Henri Poincaré and...
to make possible effective calculation of the global sections of a sheaf F. This is the main step, in numerous areas, from sheaf theory as a description of a geometric problem, to its use as a tool capable of calculating dimensions of important geometric invariants.
Its development was rapid in the years after 1950, when it was realised that sheaf cohomology was connected with more classical methods applied to the Riemann-Roch theorem, the analysis of a linear system of divisors
Linear system of divisors
In algebraic geometry, a linear system of divisors is an algebraic generalization of the geometric notion of a family of curves; the dimension of the linear system corresponds to the number of parameters of the family....
in algebraic geometry
Algebraic geometry
Algebraic geometry is a branch of mathematics which combines techniques of abstract algebra, especially commutative algebra, with the language and the problems of geometry. It occupies a central place in modern mathematics and has multiple conceptual connections with such diverse fields as complex...
, several complex variables
Several complex variables
The theory of functions of several complex variables is the branch of mathematics dealing with functionson the space Cn of n-tuples of complex numbers...
, and Hodge theory
Hodge theory
In mathematics, Hodge theory, named after W. V. D. Hodge, is one aspect of the study of the algebraic topology of a smooth manifold M. More specifically, it works out the consequences for the cohomology groups of M, with real coefficients, of the partial differential equation theory of generalised...
. The dimensions or ranks of sheaf cohomology groups became a fresh source of geometric data, or gave rise to new interpretations of older work.
The approach of Čech cohomology
The first version of sheaf cohomology to be defined was that based on Čech cohomologyCech cohomology
In mathematics, specifically algebraic topology, Čech cohomology is a cohomology theory based on the intersection properties of open covers of a topological space. It is named for the mathematician Eduard Čech.-Motivation:...
, in which the relatively small change was made of attributing to an open set
Open set
The concept of an open set is fundamental to many areas of mathematics, especially point-set topology and metric topology. Intuitively speaking, a set U is open if any point x in U can be "moved" a small amount in any direction and still be in the set U...
U of a topological space
Topological space
Topological spaces are mathematical structures that allow the formal definition of concepts such as convergence, connectedness, and continuity. They appear in virtually every branch of modern mathematics and are a central unifying notion...
X an abelian group F(U) that 'varies' with U, rather than an abelian group A that is fixed ahead of time. This means that cochains are easy to write down rather concretely; in fact the model applications, such as the Cousin problems
Cousin problems
In mathematics, the Cousin problems are two questions in several complex variables, concerning the existence of meromorphic functions that are specified in terms of local data. They were introduced in special cases by P. Cousin in 1895...
on meromorphic function
Meromorphic function
In complex analysis, a meromorphic function on an open subset D of the complex plane is a function that is holomorphic on all D except a set of isolated points, which are poles for the function...
s, stay within fairly familiar mathematical territory. From the sheaf point of view, the Čech theory is the restriction to the theory of sheaves of locally constant function
Locally constant function
In mathematics, a function f from a topological space A to a set B is called locally constant, if for every a in A there exists a neighborhood U of a, such that f is constant on U....
s with values in A. Within sheaf theory it is easy to see that 'twisted' versions, with local coefficients
Local coefficients
In mathematics, local coefficients is an idea from algebraic topology, a kind of half-way stage between homology theory or cohomology theory with coefficients in the usual sense, in a fixed abelian group A, and general sheaf cohomology which, roughly speaking, allows coefficients to vary from point...
on which the fundamental group
Fundamental group
In mathematics, more specifically algebraic topology, the fundamental group is a group associated to any given pointed topological space that provides a way of determining when two paths, starting and ending at a fixed base point, can be continuously deformed into each other...
acts, are also subsumed — along with some very different sorts of more general coefficients.
One problem with that theory was that Čech cohomology itself fails to have good properties, unless X itself is well-behaved
Well-behaved
Mathematicians very frequently speak of whether a mathematical object — a function, a set, a space of one sort or another — is "well-behaved" or not. The term has no fixed formal definition, and is dependent on mathematical interests, fashion, and taste...
. This is not a difficulty in case X is something like a manifold
Manifold
In mathematics , a manifold is a topological space that on a small enough scale resembles the Euclidean space of a specific dimension, called the dimension of the manifold....
; but embarrassing for applications to algebraic geometry, since the Zariski topology
Zariski topology
In algebraic geometry, the Zariski topology is a particular topology chosen for algebraic varieties that reflects the algebraic nature of their definition. It is due to Oscar Zariski and took a place of particular importance in the field around 1950...
is in general not Hausdorff
Hausdorff space
In topology and related branches of mathematics, a Hausdorff space, separated space or T2 space is a topological space in which distinct points have disjoint neighbourhoods. Of the many separation axioms that can be imposed on a topological space, the "Hausdorff condition" is the most frequently...
. The problem with the Čech theory manifests itself in the failure of the long exact sequence of cohomology groups associated to a short exact sequence of sheaves. This in practice is the basic method of attacking a calculation (i.e. to show how a given sheaf is involved with others in a short exact sequence, and draw consequences). The theory stood in this state of disarray only for a short while: Jean-Pierre Serre
Jean-Pierre Serre
Jean-Pierre Serre is a French mathematician. He has made contributions in the fields of algebraic geometry, number theory, and topology.-Early years:...
showed that the Čech theory worked, and on the other hand Alexandre Grothendieck proposed a more abstract definition that would build in the long exact sequence.
Definition by derived functors
The Grothendieck definition clarified the status of sheaf cohomology of a topological space X with coefficients in a sheaf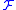 as the right derived functorDerived functor
In mathematics, certain functors may be derived to obtain other functors closely related to the original ones. This operation, while fairly abstract, unifies a number of constructions throughout mathematics.- Motivation :...
of the global section
Sheaf (mathematics)
In mathematics, a sheaf is a tool for systematically tracking locally defined data attached to the open sets of a topological space. The data can be restricted to smaller open sets, and the data assigned to an open set is equivalent to all collections of compatible data assigned to collections of...
functor:
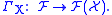
This functor is not an exact functor
Exact functor
In homological algebra, an exact functor is a functor, from some category to another, which preserves exact sequences. Exact functors are very convenient in algebraic calculations, roughly speaking because they can be applied to presentations of objects easily...
, a fact familiar in other terms from the theory of branch cuts (for example, in the case of the logarithm
Logarithm
The logarithm of a number is the exponent by which another fixed value, the base, has to be raised to produce that number. For example, the logarithm of 1000 to base 10 is 3, because 1000 is 10 to the power 3: More generally, if x = by, then y is the logarithm of x to base b, and is written...
of a complex number
Complex number
A complex number is a number consisting of a real part and an imaginary part. Complex numbers extend the idea of the one-dimensional number line to the two-dimensional complex plane by using the number line for the real part and adding a vertical axis to plot the imaginary part...
: see exponential sequence). It is a left exact functor, and therefore has a sequence of right derived functor
Functor
In category theory, a branch of mathematics, a functor is a special type of mapping between categories. Functors can be thought of as homomorphisms between categories, or morphisms when in the category of small categories....
s, denoted by
The existence
Existence theorem
In mathematics, an existence theorem is a theorem with a statement beginning 'there exist ..', or more generally 'for all x, y, ... there exist ...'. That is, in more formal terms of symbolic logic, it is a theorem with a statement involving the existential quantifier. Many such theorems will not...
of these derived functors is supplied by homological algebra
Homological algebra
Homological algebra is the branch of mathematics which studies homology in a general algebraic setting. It is a relatively young discipline, whose origins can be traced to investigations in combinatorial topology and abstract algebra at the end of the 19th century, chiefly by Henri Poincaré and...
of the abelian category
Abelian category
In mathematics, an abelian category is a category in which morphisms and objects can be added and in which kernels and cokernels exist and have desirable properties. The motivating prototype example of an abelian category is the category of abelian groups, Ab. The theory originated in a tentative...
of sheaves (and indeed this was a main reason to set up that theory). It depends on having injective resolutions; that is, in theory calculations can be done with injective resolutions, though in practice short and long exact sequences may be a better idea.
Because the derived functor can be computed by applying the functor to any acyclic resolution and keeping the cohomology of the complex, there are a number of other ways to compute cohomology groups. Depending on the concrete situation, fine, flasque, soft or acyclic sheaves are used to calculate concrete cohomology groups -- see injective sheaves
Injective sheaf
In mathematics, injective sheaves of abelian groups are used to construct the resolutions needed to define sheaf cohomology ....
.
Applications
Subsequently there were further technical extensions (for example in Godement's book), and areas of application. For example, sheaves were applied to transformation groups; as an inspiration to homology theoryHomology theory
In mathematics, homology theory is the axiomatic study of the intuitive geometric idea of homology of cycles on topological spaces. It can be broadly defined as the study of homology theories on topological spaces.-The general idea:...
in the form of Borel-Moore homology
Borel-Moore homology
In mathematics, Borel−Moore homology or homology with closed support is a homology theory for locally compact spaces, introduced by .For compact spaces, the Borel−Moore homology coincide with the usual singular homology, but for non-compact spaces, it usually gives homology groups with better...
for locally compact space
Locally compact space
In topology and related branches of mathematics, a topological space is called locally compact if, roughly speaking, each small portion of the space looks like a small portion of a compact space.-Formal definition:...
s; to representation theory
Representation theory
Representation theory is a branch of mathematics that studies abstract algebraic structures by representing their elements as linear transformations of vector spaces, and studiesmodules over these abstract algebraic structures...
in the Borel-Bott-Weil theorem; as well as becoming standard in algebraic geometry and complex manifold
Complex manifold
In differential geometry, a complex manifold is a manifold with an atlas of charts to the open unit disk in Cn, such that the transition maps are holomorphic....
s.
The particular needs of étale cohomology
Étale cohomology
In mathematics, the étale cohomology groups of an algebraic variety or scheme are algebraic analogues of the usual cohomology groups with finite coefficients of a topological space, introduced by Grothendieck in order to prove the Weil conjectures...
were more about reinterpreting sheaf in sheaf cohomology, than cohomology, given that the derived functor approach applied. Flat cohomology, crystalline cohomology
Crystalline cohomology
In mathematics, crystalline cohomology is a Weil cohomology theory for schemes introduced by and developed by . Its values are modules over rings of Witt vectors over the base field....
and successors are also applications of the basic model.
Euler characteristics
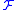The Euler characteristic of a sheaf is defined by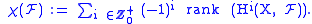To make sense of this expression, which generalises the Euler characteristic
Euler characteristic
In mathematics, and more specifically in algebraic topology and polyhedral combinatorics, the Euler characteristic is a topological invariant, a number that describes a topological space's shape or structure regardless of the way it is bent...
as alternating sum of Betti number
Betti number
In algebraic topology, a mathematical discipline, the Betti numbers can be used to distinguish topological spaces. Intuitively, the first Betti number of a space counts the maximum number of cuts that can be made without dividing the space into two pieces....
s, two conditions must be fulfilled. Firstly the summands must be almost all
Almost all
In mathematics, the phrase "almost all" has a number of specialised uses."Almost all" is sometimes used synonymously with "all but finitely many" or "all but a countable set" ; see almost....
zero, i.e. zero for
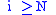for some . Further, rank must be some well-defined function from module theory, such as rank of an abelian groupRank of an abelian group
In mathematics, the rank, Prüfer rank, or torsion-free rank of an abelian group A is the cardinality of a maximal linearly independent subset. The rank of A determines the size of the largest free abelian group contained in A. If A is torsion-free then it embeds into a vector space over the...
or vector space dimension, that yields finite values on the cohomology groups in question. Therefore finiteness theorems of two kinds are required.
In theories such as coherent cohomology, where such theorems exist, the value of χ(F) is typically easier to compute, from other considerations (for example the Hirzebruch-Riemann-Roch theorem
Hirzebruch-Riemann-Roch theorem
In mathematics, the Hirzebruch–Riemann–Roch theorem, named after Friedrich Hirzebruch, Bernhard Riemann, and Gustav Roch, is Hirzebruch's 1954 result contributing to the Riemann–Roch problem for complex algebraic varieties of all dimensions...
or Grothendieck-Riemann-Roch theorem), than the individual ranks separately. In practice it is often H0(X,F) that is of most interest; one way to compute its rank is then by means of a vanishing theorem
Vanishing theorem
In algebraic geometry, a vanishing theorem gives conditions for coherent cohomology groups to vanish.*Grauert–Riemenschneider vanishing theorem*Kawamata–Viehweg vanishing theorem*Kollár vanishing theorem*Kodaira vanishing theorem*Miyaoka vanishing theorem...
on the other Hi(X,F). This is a standard indirect method of sheaf theory to produce numerical results.