Relative homology
Encyclopedia
In algebraic topology
, a branch of mathematics
, the (singular) homology of a topological space relative to a subspace is a construction in singular homology
, for pairs of spaces. The relative homology is useful and important in several ways. Intuitively, it helps determine what part of an absolute homology group comes from which subspace.
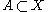, one may form the short exact sequence
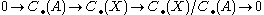
where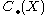
denotes the singular chains on the space X. The boundary map on 
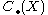leaves 
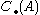invariant and therefore descends to a boundary map on the quotient. The corresponding homology is called relative homology:
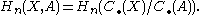
One says that relative homology is given by the relative cycles, chains whose boundaries are chains on A, modulo the relative boundaries (chains that are homologous to a chain on A, i.e. chains that would be boundaries, modulo A again).
then yields a long exact sequence
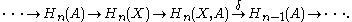
The connecting map δ takes a relative cycle, representing a homology class in Hn(X, A), to its boundary (which is a cycle in A).
It follows that Hn(X, x0), where x0 is a point in X, is the n-th reduced homology
group of X. In other words, Hi(X, x0) = Hi(X) for all i > 0. When i = 0, H0(X, x0) is the free module of one rank less than H0(X). The connected component containing x0 becomes trivial in relative homology.
The excision theorem
says that removing a sufficiently nice subset Z ⊂ A leaves the relative homology groups Hn(X, A) unchanged. Using the long exact sequence of pairs and the excision theorem, one can show that Hn(X, A) is the same as the n-th reduced homology groups of the quotient space X/A.
The n-th local homology group of a space X at a point x0 is defined to be Hn(X, X - {x0}). Informally, this is the "local" homology of X close to x0.
Relative homology readily extends to the triple (X, Y, Z) for Z ⊂ Y ⊂ X.
One can define the Euler characteristic
for a pair Y ⊂ X by
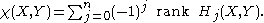
The exactness of the sequence implies that the Euler characteristic is additive, i.e. if Z ⊂ Y ⊂ X, one has
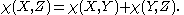
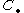can be considered to be a functor
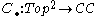
where Top2 is the category of pairs of topological spaces and
is the category chain complexes of abelian groups.
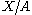. In the case that 
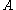is a subspace of 
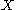fulfilling the mild regularity condition that there exists a neighborhood of 
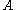that has 
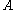as a deformation retract, then the group 
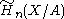is isomorphic to 
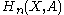. We can immediately use this fact to compute the homology of a sphere. We can realize 
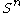as the quotient of an n-disk by its boundary, i.e. 
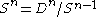. Applying the exact sequence of relative homology gives the following:
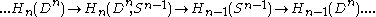
Because the disk is contractible, we know its homology groups vanish in all dimensions, so the above sequence collapses to the short exact sequence:
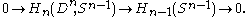
Therefore, we get isomorphisms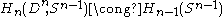
. We can now proceed by induction to show that 
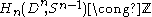. Now because 
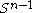is the deformation retract of a suitable neighborhood of 
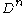, we get that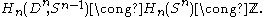 
Algebraic topology
Algebraic topology is a branch of mathematics which uses tools from abstract algebra to study topological spaces. The basic goal is to find algebraic invariants that classify topological spaces up to homeomorphism, though usually most classify up to homotopy equivalence.Although algebraic topology...
, a branch of mathematics
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the (singular) homology of a topological space relative to a subspace is a construction in singular homology
Singular homology
In algebraic topology, a branch of mathematics, singular homology refers to the study of a certain set of algebraic invariants of a topological space X, the so-called homology groups H_n....
, for pairs of spaces. The relative homology is useful and important in several ways. Intuitively, it helps determine what part of an absolute homology group comes from which subspace.
Definition
Given a subspace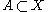, one may form the short exact sequence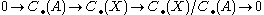where
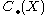denotes the singular chains on the space X. The boundary map on 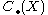leaves 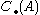invariant and therefore descends to a boundary map on the quotient. The corresponding homology is called relative homology: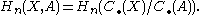One says that relative homology is given by the relative cycles, chains whose boundaries are chains on A, modulo the relative boundaries (chains that are homologous to a chain on A, i.e. chains that would be boundaries, modulo A again).
Properties
The above short exact sequences specifying the relative chain groups gives rise to a chain complex of short exact sequences. An application of the snake lemmaSnake lemma
The snake lemma is a tool used in mathematics, particularly homological algebra, to construct long exact sequences. The snake lemma is valid in every abelian category and is a crucial tool in homological algebra and its applications, for instance in algebraic topology...
then yields a long exact sequence
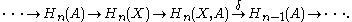
The connecting map δ takes a relative cycle, representing a homology class in Hn(X, A), to its boundary (which is a cycle in A).
It follows that Hn(X, x0), where x0 is a point in X, is the n-th reduced homology
Reduced homology
In mathematics, reduced homology is a minor modification made to homology theory in algebraic topology, designed to make a point have all its homology groups zero...
group of X. In other words, Hi(X, x0) = Hi(X) for all i > 0. When i = 0, H0(X, x0) is the free module of one rank less than H0(X). The connected component containing x0 becomes trivial in relative homology.
The excision theorem
Excision theorem
In algebraic topology, a branch of mathematics, the excision theorem is a useful theorem about relative homology—given topological spaces X and subspaces A and U such that U is also a subspace of A, the theorem says that under certain circumstances, we can cut out U from both spaces such...
says that removing a sufficiently nice subset Z ⊂ A leaves the relative homology groups Hn(X, A) unchanged. Using the long exact sequence of pairs and the excision theorem, one can show that Hn(X, A) is the same as the n-th reduced homology groups of the quotient space X/A.
The n-th local homology group of a space X at a point x0 is defined to be Hn(X, X - {x0}). Informally, this is the "local" homology of X close to x0.
Relative homology readily extends to the triple (X, Y, Z) for Z ⊂ Y ⊂ X.
One can define the Euler characteristic
Euler characteristic
In mathematics, and more specifically in algebraic topology and polyhedral combinatorics, the Euler characteristic is a topological invariant, a number that describes a topological space's shape or structure regardless of the way it is bent...
for a pair Y ⊂ X by
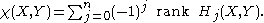
The exactness of the sequence implies that the Euler characteristic is additive, i.e. if Z ⊂ Y ⊂ X, one has
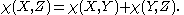
Functoriality
The map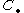 can be considered to be a functorFunctor
In category theory, a branch of mathematics, a functor is a special type of mapping between categories. Functors can be thought of as homomorphisms between categories, or morphisms when in the category of small categories....
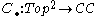
where Top2 is the category of pairs of topological spaces and
is the category chain complexes of abelian groups.Examples
One important use of relative homology is the computation of the homology groups of quotient spaces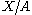. In the case that 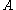is a subspace of 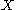fulfilling the mild regularity condition that there exists a neighborhood of 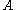that has 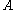as a deformation retract, then the group 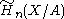is isomorphic to 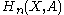. We can immediately use this fact to compute the homology of a sphere. We can realize 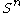as the quotient of an n-disk by its boundary, i.e. 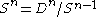. Applying the exact sequence of relative homology gives the following: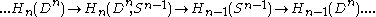Because the disk is contractible, we know its homology groups vanish in all dimensions, so the above sequence collapses to the short exact sequence:
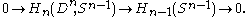
Therefore, we get isomorphisms
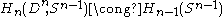. We can now proceed by induction to show that 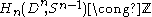. Now because 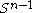is the deformation retract of a suitable neighborhood of 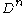, we get that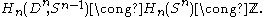 See also
- Relative contact homologyRelative contact homologyIn mathematics, in the area of symplectic topology, relative contact homology is an invariant of spaces together with a chosen subspace. Namely, it is associated to a contact manifold and one of its Legendrian submanifolds...
- Excision TheoremExcision theoremIn algebraic topology, a branch of mathematics, the excision theorem is a useful theorem about relative homology—given topological spaces X and subspaces A and U such that U is also a subspace of A, the theorem says that under certain circumstances, we can cut out U from both spaces such...
- Mayer–Vietoris sequence