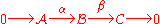
Zig-zag lemma
Encyclopedia
In mathematics
, particularly homological algebra
, the zig-zag lemma asserts the existence of a particular long exact sequence in the homology groups of certain chain complex
es. The result is valid in every abelian category
.
s or the category of vector space
s over a given field), let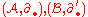 and
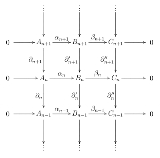
and 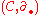 be chain complexes that fit into the following short exact sequence:
be chain complexes that fit into the following short exact sequence:
Such a sequence is shorthand for the following commutative diagram
:
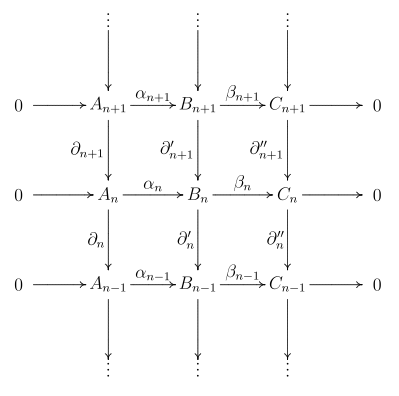
where the rows are exact sequence
s and each column is a complex
.
The zig-zag lemma asserts that there is a collection of boundary maps
that makes the following sequence exact:
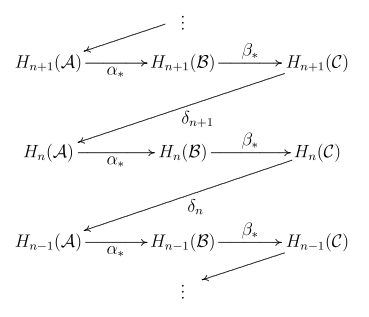
The maps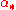 and
and 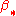 are the usual maps induced by homology. The boundary maps
are the usual maps induced by homology. The boundary maps 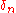 are explained below. The name of the lemma arises from the "zig-zag" behavior of the maps in the sequence. In an unfortunate overlap in terminology, this theorem is also commonly known as the "snake lemma
are explained below. The name of the lemma arises from the "zig-zag" behavior of the maps in the sequence. In an unfortunate overlap in terminology, this theorem is also commonly known as the "snake lemma
," although there is another result in homological algebra with that name. Interestingly, the "other" snake lemma can be used to prove the zig-zag lemma, in a manner different from what is described below.
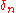 are defined using a standard diagram chasing argument. Let
are defined using a standard diagram chasing argument. Let  represent a class in
represent a class in 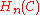 , so
, so  . Exactness of the row implies that
. Exactness of the row implies that  is surjective, so there must be some
is surjective, so there must be some  with
with 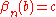 . By commutativity of the diagram,
. By commutativity of the diagram,

By exactness,
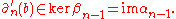
Thus, since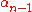 is injective, there is a unique element
is injective, there is a unique element 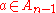 such that
such that 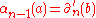 . This is a cycle, since
. This is a cycle, since 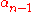 is injective and
is injective and

since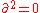 . That is,
. That is,  . This means
. This means  is a cycle, so it represents a class in
is a cycle, so it represents a class in 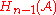 . We can now define
. We can now define

With the boundary maps defined, one can show that they are well-defined (that is, independent of the choices of c and b). The proof uses diagram chasing arguments similar to that above. Such arguments are also used to show that the sequence in homology is exact at each group.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, particularly homological algebra
Homological algebra
Homological algebra is the branch of mathematics which studies homology in a general algebraic setting. It is a relatively young discipline, whose origins can be traced to investigations in combinatorial topology and abstract algebra at the end of the 19th century, chiefly by Henri Poincaré and...
, the zig-zag lemma asserts the existence of a particular long exact sequence in the homology groups of certain chain complex
Chain complex
In mathematics, chain complex and cochain complex are constructs originally used in the field of algebraic topology. They are algebraic means of representing the relationships between the cycles and boundaries in various dimensions of some "space". Here the "space" could be a topological space or...
es. The result is valid in every abelian category
Abelian category
In mathematics, an abelian category is a category in which morphisms and objects can be added and in which kernels and cokernels exist and have desirable properties. The motivating prototype example of an abelian category is the category of abelian groups, Ab. The theory originated in a tentative...
.
Statement
In an abelian category (such as the category of abelian groupAbelian group
In abstract algebra, an abelian group, also called a commutative group, is a group in which the result of applying the group operation to two group elements does not depend on their order . Abelian groups generalize the arithmetic of addition of integers...
s or the category of vector space
Vector space
A vector space is a mathematical structure formed by a collection of vectors: objects that may be added together and multiplied by numbers, called scalars in this context. Scalars are often taken to be real numbers, but one may also consider vector spaces with scalar multiplication by complex...
s over a given field), let
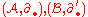 and
and 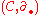 be chain complexes that fit into the following short exact sequence:
be chain complexes that fit into the following short exact sequence:Such a sequence is shorthand for the following commutative diagram
Commutative diagram
In mathematics, and especially in category theory, a commutative diagram is a diagram of objects and morphisms such that all directed paths in the diagram with the same start and endpoints lead to the same result by composition...
:

where the rows are exact sequence
Exact sequence
An exact sequence is a concept in mathematics, especially in homological algebra and other applications of abelian category theory, as well as in differential geometry and group theory...
s and each column is a complex
Chain complex
In mathematics, chain complex and cochain complex are constructs originally used in the field of algebraic topology. They are algebraic means of representing the relationships between the cycles and boundaries in various dimensions of some "space". Here the "space" could be a topological space or...
.
The zig-zag lemma asserts that there is a collection of boundary maps
that makes the following sequence exact:

The maps
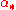 and
and 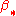 are the usual maps induced by homology. The boundary maps
are the usual maps induced by homology. The boundary maps 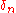 are explained below. The name of the lemma arises from the "zig-zag" behavior of the maps in the sequence. In an unfortunate overlap in terminology, this theorem is also commonly known as the "snake lemma
are explained below. The name of the lemma arises from the "zig-zag" behavior of the maps in the sequence. In an unfortunate overlap in terminology, this theorem is also commonly known as the "snake lemmaSnake lemma
The snake lemma is a tool used in mathematics, particularly homological algebra, to construct long exact sequences. The snake lemma is valid in every abelian category and is a crucial tool in homological algebra and its applications, for instance in algebraic topology...
," although there is another result in homological algebra with that name. Interestingly, the "other" snake lemma can be used to prove the zig-zag lemma, in a manner different from what is described below.
Construction of the boundary maps
The maps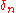 are defined using a standard diagram chasing argument. Let
are defined using a standard diagram chasing argument. Let  represent a class in
represent a class in 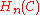 , so
, so  . Exactness of the row implies that
. Exactness of the row implies that  is surjective, so there must be some
is surjective, so there must be some  with
with 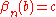 . By commutativity of the diagram,
. By commutativity of the diagram,
By exactness,
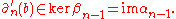
Thus, since
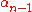 is injective, there is a unique element
is injective, there is a unique element 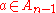 such that
such that 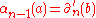 . This is a cycle, since
. This is a cycle, since 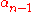 is injective and
is injective and
since
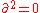 . That is,
. That is,  . This means
. This means  is a cycle, so it represents a class in
is a cycle, so it represents a class in 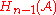 . We can now define
. We can now define
With the boundary maps defined, one can show that they are well-defined (that is, independent of the choices of c and b). The proof uses diagram chasing arguments similar to that above. Such arguments are also used to show that the sequence in homology is exact at each group.