
Invariant measure
Encyclopedia
In mathematics
, an invariant measure is a measure
that is preserved by some function
. Ergodic theory
is the study of invariant measures in dynamical systems. The Krylov–Bogolyubov theorem proves the existence of invariant measures under certain conditions on the function and space under consideration.
from X to itself. A measure μ on (X, Σ) is said to be invariant under f if, for every measurable set A in Σ,

In terms of the push forward
, this states that f∗(μ) = μ.
The collection of measures (usually probability measure
s) on X that are invariant under f is sometimes denoted Mf(X). The collection of ergodic measures
, Ef(X), is a subset of Mf(X). Moreover, any convex combination
of two invariant measures is also invariant, so Mf(X) is a convex set
; Ef(X) consists precisely of the extreme points of Mf(X).
In the case of a dynamical system
(X, T, φ), where (X, Σ) is a measurable space as before, T is a monoid
and φ : T × X → X is the flow map, a measure μ on (X, Σ) is said to be an invariant measure if it is an invariant measure for each map φt : X → X. Explicitly, μ is invariant if and only if
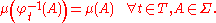
Put another way, μ is an invariant measure for a sequence of random variable
s (Zt)t≥0 (perhaps a Markov chain
or the solution to a stochastic differential equation
) if, whenever the initial condition Z0 is distributed according to μ, so is Zt for any later time t.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, an invariant measure is a measure
Measure (mathematics)
In mathematical analysis, a measure on a set is a systematic way to assign to each suitable subset a number, intuitively interpreted as the size of the subset. In this sense, a measure is a generalization of the concepts of length, area, and volume...
that is preserved by some function
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
. Ergodic theory
Ergodic theory
Ergodic theory is a branch of mathematics that studies dynamical systems with an invariant measure and related problems. Its initial development was motivated by problems of statistical physics....
is the study of invariant measures in dynamical systems. The Krylov–Bogolyubov theorem proves the existence of invariant measures under certain conditions on the function and space under consideration.
Definition
Let (X, Σ) be a measurable space and let f be a measurable functionMeasurable function
In mathematics, particularly in measure theory, measurable functions are structure-preserving functions between measurable spaces; as such, they form a natural context for the theory of integration...
from X to itself. A measure μ on (X, Σ) is said to be invariant under f if, for every measurable set A in Σ,

In terms of the push forward
Pushforward measure
In measure theory, a pushforward measure is obtained by transferring a measure from one measurable space to another using a measurable function.-Definition:...
, this states that f∗(μ) = μ.
The collection of measures (usually probability measure
Probability measure
In mathematics, a probability measure is a real-valued function defined on a set of events in a probability space that satisfies measure properties such as countable additivity...
s) on X that are invariant under f is sometimes denoted Mf(X). The collection of ergodic measures
Ergodic (adjective)
In mathematics, the term ergodic is used to describe a dynamical system which, broadly speaking, has the same behavior averaged over time as averaged over space. In physics the term is used to imply that a system satisfies the ergodic hypothesis of thermodynamics.-Etymology:The word ergodic is...
, Ef(X), is a subset of Mf(X). Moreover, any convex combination
Convex combination
In convex geometry, a convex combination is a linear combination of points where all coefficients are non-negative and sum up to 1....
of two invariant measures is also invariant, so Mf(X) is a convex set
Convex set
In Euclidean space, an object is convex if for every pair of points within the object, every point on the straight line segment that joins them is also within the object...
; Ef(X) consists precisely of the extreme points of Mf(X).
In the case of a dynamical system
Dynamical system (definition)
The dynamical system concept is a mathematical formalization for any fixed "rule" which describes the time dependence of a point's position in its ambient space...
(X, T, φ), where (X, Σ) is a measurable space as before, T is a monoid
Monoid
In abstract algebra, a branch of mathematics, a monoid is an algebraic structure with a single associative binary operation and an identity element. Monoids are studied in semigroup theory as they are naturally semigroups with identity. Monoids occur in several branches of mathematics; for...
and φ : T × X → X is the flow map, a measure μ on (X, Σ) is said to be an invariant measure if it is an invariant measure for each map φt : X → X. Explicitly, μ is invariant if and only if
If and only if
In logic and related fields such as mathematics and philosophy, if and only if is a biconditional logical connective between statements....
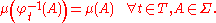
Put another way, μ is an invariant measure for a sequence of random variable
Random variable
In probability and statistics, a random variable or stochastic variable is, roughly speaking, a variable whose value results from a measurement on some type of random process. Formally, it is a function from a probability space, typically to the real numbers, which is measurable functionmeasurable...
s (Zt)t≥0 (perhaps a Markov chain
Markov chain
A Markov chain, named after Andrey Markov, is a mathematical system that undergoes transitions from one state to another, between a finite or countable number of possible states. It is a random process characterized as memoryless: the next state depends only on the current state and not on the...
or the solution to a stochastic differential equation
Stochastic differential equation
A stochastic differential equation is a differential equation in which one or more of the terms is a stochastic process, thus resulting in a solution which is itself a stochastic process....
) if, whenever the initial condition Z0 is distributed according to μ, so is Zt for any later time t.
Examples
- Consider the real lineReal lineIn mathematics, the real line, or real number line is the line whose points are the real numbers. That is, the real line is the set of all real numbers, viewed as a geometric space, namely the Euclidean space of dimension one...
R with its usual Borel σ-algebra; fix a ∈ R and consider the translation map Ta : R → R given by:
- Then one-dimensional Lebesgue measureLebesgue measureIn measure theory, the Lebesgue measure, named after French mathematician Henri Lebesgue, is the standard way of assigning a measure to subsets of n-dimensional Euclidean space. For n = 1, 2, or 3, it coincides with the standard measure of length, area, or volume. In general, it is also called...
λ is an invariant measure for Ta.
- More generally, on n-dimensional Euclidean spaceEuclidean spaceIn mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
Rn with its usual Borel σ-algebra, n-dimensional Lebesgue measure λn is an invariant measure for any isometryIsometryIn mathematics, an isometry is a distance-preserving map between metric spaces. Geometric figures which can be related by an isometry are called congruent.Isometries are often used in constructions where one space is embedded in another space...
of Euclidean space, i.e. a map T : Rn → Rn that can be written as
- for some n × n orthogonal matrixOrthogonal matrixIn linear algebra, an orthogonal matrix , is a square matrix with real entries whose columns and rows are orthogonal unit vectors ....
A ∈ O(n) and a vector b ∈ Rn.
- The invariant measure in the first example is unique up to trivial renormalization with a constant factor. This does not have to be necessarily the case: Consider a set consisting of just two points
 and the identity map
and the identity map 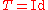 which leaves each point fixed. Then any probability measure
which leaves each point fixed. Then any probability measure  is invariant. Note that S trivially has a decomposition into T-invariant components {A} and {B}.
is invariant. Note that S trivially has a decomposition into T-invariant components {A} and {B}.



