
Equilibrium point
Encyclopedia
In mathematics
, the point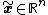 is an equilibrium point for the differential equation
is an equilibrium point for the differential equation
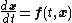
if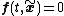 for all
for all  .
.
Similarly, the point is an equilibrium point (or fixed point
is an equilibrium point (or fixed point
) for the difference equation

if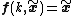 for
for 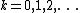 .
.
Equilibria can be classified by looking at the signs of the eigenvalues of the linearization of the equations about the equilibria. That is to say, by evaluating the Jacobian matrix at each of the equilibrium points of the system, and then finding the resulting eigenvalues, the equilibria can be categorized. Then the behavior of the system in the neighborhood of each equilibrium point can be qualitatively determined, (or even quantitatively determined, in some instances, by finding the eigenvector(s) associated with each eigenvalue).
An equilibrium point is hyperbolic if none of the eigenvalues have zero real part. If all eigenvalues have negative real part, the equilibrium is a stable node. If at least one has a positive real part, the equilibrium is an unstable node. If at least one eigenvalue has negative real part and at least one has positive real part, the equilibrium is a saddle point
.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, the point
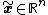 is an equilibrium point for the differential equation
is an equilibrium point for the differential equationDifferential equation
A differential equation is a mathematical equation for an unknown function of one or several variables that relates the values of the function itself and its derivatives of various orders...
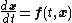
if
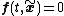 for all
for all  .
.Similarly, the point
 is an equilibrium point (or fixed point
is an equilibrium point (or fixed pointFixed point (mathematics)
In mathematics, a fixed point of a function is a point that is mapped to itself by the function. A set of fixed points is sometimes called a fixed set...
) for the difference equation

if
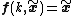 for
for 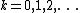 .
.Equilibria can be classified by looking at the signs of the eigenvalues of the linearization of the equations about the equilibria. That is to say, by evaluating the Jacobian matrix at each of the equilibrium points of the system, and then finding the resulting eigenvalues, the equilibria can be categorized. Then the behavior of the system in the neighborhood of each equilibrium point can be qualitatively determined, (or even quantitatively determined, in some instances, by finding the eigenvector(s) associated with each eigenvalue).
An equilibrium point is hyperbolic if none of the eigenvalues have zero real part. If all eigenvalues have negative real part, the equilibrium is a stable node. If at least one has a positive real part, the equilibrium is an unstable node. If at least one eigenvalue has negative real part and at least one has positive real part, the equilibrium is a saddle point
Saddle point
In mathematics, a saddle point is a point in the domain of a function that is a stationary point but not a local extremum. The name derives from the fact that in two dimensions the surface resembles a saddle that curves up in one direction, and curves down in a different direction...
.

