
Distance (graph theory)
Encyclopedia
In the mathematical
field of graph theory
, the distance between two vertices
in a graph
is the number of edges in a shortest path
connecting them. This is also known as the geodesic distance
because it is the length of the graph geodesic between those two vertices. If there is no path connecting the two vertices, i.e., if they belong to different connected component
s, then conventionally the distance is defined as infinite.
The vertex set (of an undirected graph) and the distance function form a metric space
, if and only if the graph is connected.
A metric
defined over a set of points in terms of distances in a graph defined over the set is called a graph metric.
There are a number of other measurements defined in terms of distance:
The eccentricity of a vertex
of a vertex  is the greatest geodesic distance between
is the greatest geodesic distance between  and any other vertex. It can be thought of as how far a node is from the node most distant from it in the graph.
and any other vertex. It can be thought of as how far a node is from the node most distant from it in the graph.
The radius of a graph is the minimum eccentricity of any vertex.
The diameter of a graph is the maximum eccentricity of any vertex in the graph. That is, it is the greatest distance between any pair of vertices. To find the diameter of a graph, first find the shortest path
between each pair of vertices
. The greatest length of any of these paths is the diameter of the graph.
A central vertex in a graph of radius is one whose eccentricity is
is one whose eccentricity is  —that is, a vertex that achieves the radius.
—that is, a vertex that achieves the radius.
A peripheral vertex in a graph of diameter is one that is distance
is one that is distance  from some other vertex—that is, a vertex that achieves the diameter.
from some other vertex—that is, a vertex that achieves the diameter.
A pseudo-peripheral vertex has the property that for any vertex
has the property that for any vertex  , if
, if  is as far away from
is as far away from  as possible, then
as possible, then  is as far away from
is as far away from  as possible. Formally, a vertex u is pseudo-peripheral,
as possible. Formally, a vertex u is pseudo-peripheral,
if for each vertex v with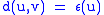 holds
holds 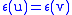 .
.
algorithms need a starting vertex with a high eccentricity. A peripheral vertex would be perfect, but is often hard to calculate. In most circumstances a pseudo-peripheral vertex can be used. A pseudo-peripheral vertex can easily be found with the following algorithm:
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
field of graph theory
Graph theory
In mathematics and computer science, graph theory is the study of graphs, mathematical structures used to model pairwise relations between objects from a certain collection. A "graph" in this context refers to a collection of vertices or 'nodes' and a collection of edges that connect pairs of...
, the distance between two vertices
Vertex (graph theory)
In graph theory, a vertex or node is the fundamental unit out of which graphs are formed: an undirected graph consists of a set of vertices and a set of edges , while a directed graph consists of a set of vertices and a set of arcs...
in a graph
Graph (mathematics)
In mathematics, a graph is an abstract representation of a set of objects where some pairs of the objects are connected by links. The interconnected objects are represented by mathematical abstractions called vertices, and the links that connect some pairs of vertices are called edges...
is the number of edges in a shortest path
Shortest path problem
In graph theory, the shortest path problem is the problem of finding a path between two vertices in a graph such that the sum of the weights of its constituent edges is minimized...
connecting them. This is also known as the geodesic distance
because it is the length of the graph geodesic between those two vertices. If there is no path connecting the two vertices, i.e., if they belong to different connected component
Connected component (graph theory)
In graph theory, a connected component of an undirected graph is a subgraph in which any two vertices are connected to each other by paths, and which is connected to no additional vertices. For example, the graph shown in the illustration on the right has three connected components...
s, then conventionally the distance is defined as infinite.
The vertex set (of an undirected graph) and the distance function form a metric space
Metric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
, if and only if the graph is connected.
A metric
Metric (mathematics)
In mathematics, a metric or distance function is a function which defines a distance between elements of a set. A set with a metric is called a metric space. A metric induces a topology on a set but not all topologies can be generated by a metric...
defined over a set of points in terms of distances in a graph defined over the set is called a graph metric.
There are a number of other measurements defined in terms of distance:
The eccentricity
 of a vertex
of a vertex  is the greatest geodesic distance between
is the greatest geodesic distance between  and any other vertex. It can be thought of as how far a node is from the node most distant from it in the graph.
and any other vertex. It can be thought of as how far a node is from the node most distant from it in the graph.The radius of a graph is the minimum eccentricity of any vertex.
The diameter of a graph is the maximum eccentricity of any vertex in the graph. That is, it is the greatest distance between any pair of vertices. To find the diameter of a graph, first find the shortest path
Shortest path problem
In graph theory, the shortest path problem is the problem of finding a path between two vertices in a graph such that the sum of the weights of its constituent edges is minimized...
between each pair of vertices
Vertex (graph theory)
In graph theory, a vertex or node is the fundamental unit out of which graphs are formed: an undirected graph consists of a set of vertices and a set of edges , while a directed graph consists of a set of vertices and a set of arcs...
. The greatest length of any of these paths is the diameter of the graph.
A central vertex in a graph of radius
 is one whose eccentricity is
is one whose eccentricity is  —that is, a vertex that achieves the radius.
—that is, a vertex that achieves the radius.A peripheral vertex in a graph of diameter
 is one that is distance
is one that is distance  from some other vertex—that is, a vertex that achieves the diameter.
from some other vertex—that is, a vertex that achieves the diameter.A pseudo-peripheral vertex
 has the property that for any vertex
has the property that for any vertex  , if
, if  is as far away from
is as far away from  as possible, then
as possible, then  is as far away from
is as far away from  as possible. Formally, a vertex u is pseudo-peripheral,
as possible. Formally, a vertex u is pseudo-peripheral,if for each vertex v with
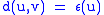 holds
holds 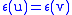 .
.Algorithm for finding pseudo-peripheral vertices
Often peripheral sparse matrixSparse matrix
In the subfield of numerical analysis, a sparse matrix is a matrix populated primarily with zeros . The term itself was coined by Harry M. Markowitz....
algorithms need a starting vertex with a high eccentricity. A peripheral vertex would be perfect, but is often hard to calculate. In most circumstances a pseudo-peripheral vertex can be used. A pseudo-peripheral vertex can easily be found with the following algorithm:
- Choose a vertex
 .
. - Among all the vertices that are as far from
 as possible, let
as possible, let  be one with minimal degreeDegree (graph theory)In graph theory, the degree of a vertex of a graph is the number of edges incident to the vertex, with loops counted twice. The degree of a vertex v is denoted \deg. The maximum degree of a graph G, denoted by Δ, and the minimum degree of a graph, denoted by δ, are the maximum and minimum degree...
be one with minimal degreeDegree (graph theory)In graph theory, the degree of a vertex of a graph is the number of edges incident to the vertex, with loops counted twice. The degree of a vertex v is denoted \deg. The maximum degree of a graph G, denoted by Δ, and the minimum degree of a graph, denoted by δ, are the maximum and minimum degree...
. - If
 then set
then set  and repeat with step 2, else
and repeat with step 2, else  is a pseudo-peripheral vertex.
is a pseudo-peripheral vertex.
See also
- Distance matrixDistance matrixIn mathematics, computer science and graph theory, a distance matrix is a matrix containing the distances, taken pairwise, of a set of points...
- Resistance distanceResistance distanceIn graph theory, the resistance distance between two vertices of a simple connected graph, G, is equal to the resistance between two equivalent points on an electrical network, constructed so as to correspond to G, with each edge being replaced by a 1 ohm resistance...
- Betweenness
- CentralityCentralityWithin graph theory and network analysis, there are various measures of the centrality of a vertex within a graph that determine the relative importance of a vertex within the graph...
- Closeness
- Degree diameter problem for graphGraph (mathematics)In mathematics, a graph is an abstract representation of a set of objects where some pairs of the objects are connected by links. The interconnected objects are represented by mathematical abstractions called vertices, and the links that connect some pairs of vertices are called edges...
s and digraphs

