
Arc length
Encyclopedia
Determining the length of an irregular arc segment is also called rectification of a curve
. Historically, many methods were used for specific curves. The advent of infinitesimal calculus
led to a general formula that provides closed-form solutions
in some cases.
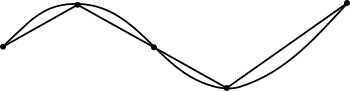 A curve
A curve
in the plane
can be approximated by connecting a finite number of points
on the curve using line segment
s to create a polygonal path
. Since it is straightforward to calculate the length
of each linear segment (using the Pythagorean theorem
in Euclidean space, for example), the total length of the approximation can be found by summing
the lengths of each linear segment.
If the curve is not already a polygonal path, better approximations to the curve can be obtained by following the shape of the curve increasingly more closely. The approach is to use an increasingly larger number of segments of smaller lengths. The lengths of the successive approximations do not decrease and will eventually keep increasing—possibly indefinitely, but for smooth curves this will tend to a limit as the lengths of the segments get arbitrarily small
.
For some curves there is a smallest number L that is an upper bound on the length of any polygonal approximation. If such a number exists, then the curve is said to be rectifiable and the curve is defined to have arc length L.
in Euclidean
(or, more generally, a metric
) space X = Rn, so C is the image
of a continuous function
f : [a, b] → X of the interval
[a, b] into X.
From a partition
a = t0 < t1 < ... < tn−1 < tn = b of the interval [a, b] we obtain a finite collection of points f(t0), f(t1), ..., f(tn−1), f(tn) on the curve C. Denote the distance
from f(ti) to f(ti+1) by d(f(ti), f(ti+1)), which is the length of the line segment
connecting the two points.
The arc length L of C is then defined to be

where the supremum
is taken over all possible partitions of [a, b] and n is unbounded.
The arc length L is either finite or infinite. If L < ∞ then we say that C is rectifiable, and is non-rectifiable otherwise. This definition of arc length does not require that C is defined by a differentiable
function. In fact in general, the notion of differentiability is not defined on a metric space.
A curve may be parameterized in many ways. Suppose C also has the parameterization g : [c, d] → X. Provided that f and g are injective, there is a continuous monotone function S from [a, b] to [c, d] so that g(S(t)) = f(t) and an inverse function S−1 from [c, d] to [a, b]. It is clear that any sum of the form
 can be made equal to a sum of the form
can be made equal to a sum of the form
 by taking
by taking  , and similarly a sum involving g can be made equal to a sum involving f. So the arc length is an intrinsic property of the curve, meaning that it does not depend on the choice of parameterization.
, and similarly a sum involving g can be made equal to a sum involving f. So the arc length is an intrinsic property of the curve, meaning that it does not depend on the choice of parameterization.
The definition of arc length for the curve is analogous to the definition of the total variation
of a real-valued function.
 such that
such that  and
and
 (its derivative with respect to x) are continuous
(its derivative with respect to x) are continuous
on [a, b]. The length s of the part of the graph of f between x = a and x = b can be found as follows:
Consider an infinitesimal part of the curve (or consider this as a limit in which the change in s approaches
(or consider this as a limit in which the change in s approaches  ). According to Pythagoras' theorem
). According to Pythagoras' theorem  , from which:
, from which:



If a curve is defined parametrically by x = X(t) and y = Y(t), then its arc length between t = a and t = b is

This is more clearly a consequence of the distance formula where instead of a and
and  , we take the limit. A useful mnemonic is
, we take the limit. A useful mnemonic is
If a function is defined in polar coordinates
by then the arc length is given by
then the arc length is given by

In most cases, including even simple curves, there are no closed-form solutions of arc length and numerical integration
is necessary.
Curves with closed-form solution for arc length include the catenary
, circle
, cycloid
, logarithmic spiral
, parabola
, semicubical parabola and (mathematically, a curve) straight line
. The lack of closed form solution for the arc length of an elliptic arc led to the development of the elliptic integral
s.
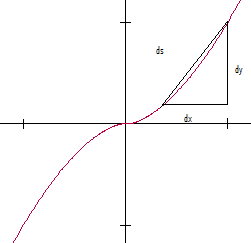 In order to approximate the arc length of the curve, it is split into many linear
In order to approximate the arc length of the curve, it is split into many linear
segments. To make the value exact, and not an approximation
, infinitely many linear elements are needed. This means that each element is infinitely small. This fact manifests itself later on when an integral
is used.
Begin by looking at a representative linear segment (see image) and observe that its length (element of the arc length) will be the differential
ds. We will call the horizontal element of this distance dx, and the vertical element dy.
The Pythagorean theorem
tells us that

Since the function is defined in time, segments (ds) are added up across infinitesimally small intervals of time (dt) yielding the integral

If y is a function of x, so that we could take t = x, then we have:

which is the arc length from x = a to x = b of the graph of the function ƒ.
For example, the curve in this figure is defined by

Subsequently, the arc length integral for values of t from -1 to 1 is

Using computational approximations, we can obtain a very accurate (but still approximate) arc length of 2.905. An expression in terms of the hypergeometric function can be obtained: it is
 , so that for each one an associated
, so that for each one an associated  exists. The length of any given hypotenuse is given by the Pythagorean Theorem
exists. The length of any given hypotenuse is given by the Pythagorean Theorem
:
The summation of the lengths of the hypotenuses approximates
hypotenuses approximates  :
:
Multiplying the radicand by produces:
produces:
Then, our previous result becomes:
As the length of these segments decreases, the approximation improves. The limit of the approximation, as
of these segments decreases, the approximation improves. The limit of the approximation, as  goes to zero, is equal to
goes to zero, is equal to  :
:
 . If we set the surface f(x,y) to 1, we will get arc length multiplied by 1, or
. If we set the surface f(x,y) to 1, we will get arc length multiplied by 1, or  . If x = t, and y = f(t), then y = f(x), from when x is a to when x is b. If we set these equations into our formula we get:
. If x = t, and y = f(t), then y = f(x), from when x is a to when x is b. If we set these equations into our formula we get:  (Note: If x = t then dt = dx). This is the arc length formula.
(Note: If x = t then dt = dx). This is the arc length formula.
is the central angle divided by 360° multiplied by the circumference
.
The circumference
of a circle is , where r is the radius, or
, where r is the radius, or  , where d is the diameter.
, where d is the diameter.
Arc lengths are denoted by s, since arcs "subtend" an angle.
If the angle measurement is in radians then where r is the radius and
where r is the radius and  is the subtended angle. The units of s will be the same as that of the radius.
is the subtended angle. The units of s will be the same as that of the radius.
In a semicircle
, .
.
, even the greatest thinkers considered it impossible to compute the length of an irregular arc. Although Archimedes
had pioneered a way of finding the area beneath a curve with his method of exhaustion
, few believed it was even possible for curves to have definite lengths, as do straight lines. The first ground was broken in this field, as it often has been in calculus
, by approximation
. People began to inscribe polygon
s within the curves and compute the length of the sides for a somewhat accurate measurement of the length. By using more segments, and by decreasing the length of each segment, they were able to obtain a more and more accurate approximation. In particular, by inscribing a polygon of many sides in a circle, they were able to find approximate values of π.
s: the logarithmic spiral
by Evangelista Torricelli
in 1645 (some sources say John Wallis in the 1650s), the cycloid
by Christopher Wren
in 1658, and the catenary
by Gottfried Leibniz
in 1691.
In 1659, Wallis credited William Neile
's discovery of the first rectification of a nontrivial algebraic curve
, the semicubical parabola.
and Pierre de Fermat
.
In 1659 van Heuraet published a construction showing that arc length could be interpreted as the area under a curve—this integral, in effect—and applied it to the parabola
. In 1660, Fermat published a more general theory containing the same result in his De linearum curvarum cum lineis rectis comparatione dissertatio geometrica.
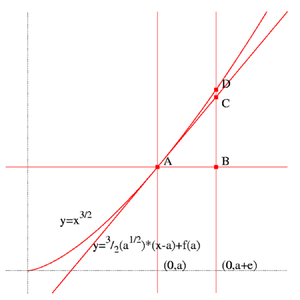 Building on his previous work with tangents, Fermat used the curve
Building on his previous work with tangents, Fermat used the curve

whose tangent
at x = a had a slope
of

so the tangent line would have the equation

Next, he increased a by a small amount to a + ε, making segment AC a relatively good approximation for the length of the curve from A to D. To find the length of the segment AC, he used the Pythagorean theorem
:
Curve
In mathematics, a curve is, generally speaking, an object similar to a line but which is not required to be straight...
. Historically, many methods were used for specific curves. The advent of infinitesimal calculus
Infinitesimal calculus
Infinitesimal calculus is the part of mathematics concerned with finding slope of curves, areas under curves, minima and maxima, and other geometric and analytic problems. It was independently developed by Gottfried Leibniz and Isaac Newton starting in the 1660s...
led to a general formula that provides closed-form solutions
Closed-form expression
In mathematics, an expression is said to be a closed-form expression if it can be expressed analytically in terms of a bounded number of certain "well-known" functions...
in some cases.
General approach

Curve
In mathematics, a curve is, generally speaking, an object similar to a line but which is not required to be straight...
in the plane
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
can be approximated by connecting a finite number of points
Point (geometry)
In geometry, topology and related branches of mathematics a spatial point is a primitive notion upon which other concepts may be defined. In geometry, points are zero-dimensional; i.e., they do not have volume, area, length, or any other higher-dimensional analogue. In branches of mathematics...
on the curve using line segment
Line segment
In geometry, a line segment is a part of a line that is bounded by two end points, and contains every point on the line between its end points. Examples of line segments include the sides of a triangle or square. More generally, when the end points are both vertices of a polygon, the line segment...
s to create a polygonal path
Polygonal chain
A polygonal chain, polygonal curve, polygonal path, or piecewise linear curve, is a connected series of line segments. More formally, a polygonal chain P is a curve specified by a sequence of points \scriptstyle called its vertices so that the curve consists of the line segments connecting the...
. Since it is straightforward to calculate the length
Length
In geometric measurements, length most commonly refers to the longest dimension of an object.In certain contexts, the term "length" is reserved for a certain dimension of an object along which the length is measured. For example it is possible to cut a length of a wire which is shorter than wire...
of each linear segment (using the Pythagorean theorem
Pythagorean theorem
In mathematics, the Pythagorean theorem or Pythagoras' theorem is a relation in Euclidean geometry among the three sides of a right triangle...
in Euclidean space, for example), the total length of the approximation can be found by summing
Summation
Summation is the operation of adding a sequence of numbers; the result is their sum or total. If numbers are added sequentially from left to right, any intermediate result is a partial sum, prefix sum, or running total of the summation. The numbers to be summed may be integers, rational numbers,...
the lengths of each linear segment.
If the curve is not already a polygonal path, better approximations to the curve can be obtained by following the shape of the curve increasingly more closely. The approach is to use an increasingly larger number of segments of smaller lengths. The lengths of the successive approximations do not decrease and will eventually keep increasing—possibly indefinitely, but for smooth curves this will tend to a limit as the lengths of the segments get arbitrarily small
Arbitrarily large
In mathematics, the phrase arbitrarily large, arbitrarily small, arbitrarily long is used in statements such as:which is shorthand for:This should not be confused with the phrase "sufficiently large"...
.
For some curves there is a smallest number L that is an upper bound on the length of any polygonal approximation. If such a number exists, then the curve is said to be rectifiable and the curve is defined to have arc length L.
Definition
Let C be a curveCurve
In mathematics, a curve is, generally speaking, an object similar to a line but which is not required to be straight...
in Euclidean
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
(or, more generally, a metric
Metric space
In mathematics, a metric space is a set where a notion of distance between elements of the set is defined.The metric space which most closely corresponds to our intuitive understanding of space is the 3-dimensional Euclidean space...
) space X = Rn, so C is the image
Image (mathematics)
In mathematics, an image is the subset of a function's codomain which is the output of the function on a subset of its domain. Precisely, evaluating the function at each element of a subset X of the domain produces a set called the image of X under or through the function...
of a continuous function
Continuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
f : [a, b] → X of the interval
Interval (mathematics)
In mathematics, a interval is a set of real numbers with the property that any number that lies between two numbers in the set is also included in the set. For example, the set of all numbers satisfying is an interval which contains and , as well as all numbers between them...
[a, b] into X.
From a partition
Partition of an interval
In mathematics, a partition, P of an interval [a, b] on the real line is a finite sequence of the formIn mathematics, a partition, P of an interval [a, b] on the real line is a finite sequence of the form...
a = t0 < t1 < ... < tn−1 < tn = b of the interval [a, b] we obtain a finite collection of points f(t0), f(t1), ..., f(tn−1), f(tn) on the curve C. Denote the distance
Distance
Distance is a numerical description of how far apart objects are. In physics or everyday discussion, distance may refer to a physical length, or an estimation based on other criteria . In mathematics, a distance function or metric is a generalization of the concept of physical distance...
from f(ti) to f(ti+1) by d(f(ti), f(ti+1)), which is the length of the line segment
Line segment
In geometry, a line segment is a part of a line that is bounded by two end points, and contains every point on the line between its end points. Examples of line segments include the sides of a triangle or square. More generally, when the end points are both vertices of a polygon, the line segment...
connecting the two points.
The arc length L of C is then defined to be

where the supremum
Supremum
In mathematics, given a subset S of a totally or partially ordered set T, the supremum of S, if it exists, is the least element of T that is greater than or equal to every element of S. Consequently, the supremum is also referred to as the least upper bound . If the supremum exists, it is unique...
is taken over all possible partitions of [a, b] and n is unbounded.
The arc length L is either finite or infinite. If L < ∞ then we say that C is rectifiable, and is non-rectifiable otherwise. This definition of arc length does not require that C is defined by a differentiable
Derivative
In calculus, a branch of mathematics, the derivative is a measure of how a function changes as its input changes. Loosely speaking, a derivative can be thought of as how much one quantity is changing in response to changes in some other quantity; for example, the derivative of the position of a...
function. In fact in general, the notion of differentiability is not defined on a metric space.
A curve may be parameterized in many ways. Suppose C also has the parameterization g : [c, d] → X. Provided that f and g are injective, there is a continuous monotone function S from [a, b] to [c, d] so that g(S(t)) = f(t) and an inverse function S−1 from [c, d] to [a, b]. It is clear that any sum of the form
 can be made equal to a sum of the form
can be made equal to a sum of the form by taking
by taking  , and similarly a sum involving g can be made equal to a sum involving f. So the arc length is an intrinsic property of the curve, meaning that it does not depend on the choice of parameterization.
, and similarly a sum involving g can be made equal to a sum involving f. So the arc length is an intrinsic property of the curve, meaning that it does not depend on the choice of parameterization.The definition of arc length for the curve is analogous to the definition of the total variation
Total variation
In mathematics, the total variation identifies several slightly different concepts, related to the structure of the codomain of a function or a measure...
of a real-valued function.
Finding arc lengths by integrating
Consider a real functionFunction (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
 such that
such that  and
and (its derivative with respect to x) are continuous
(its derivative with respect to x) are continuousContinuous function
In mathematics, a continuous function is a function for which, intuitively, "small" changes in the input result in "small" changes in the output. Otherwise, a function is said to be "discontinuous". A continuous function with a continuous inverse function is called "bicontinuous".Continuity of...
on [a, b]. The length s of the part of the graph of f between x = a and x = b can be found as follows:
Consider an infinitesimal part of the curve
 (or consider this as a limit in which the change in s approaches
(or consider this as a limit in which the change in s approaches  ). According to Pythagoras' theorem
). According to Pythagoras' theorem  , from which:
, from which:



If a curve is defined parametrically by x = X(t) and y = Y(t), then its arc length between t = a and t = b is

This is more clearly a consequence of the distance formula where instead of a
 and
and  , we take the limit. A useful mnemonic is
, we take the limit. A useful mnemonic is
If a function is defined in polar coordinates
Polar coordinate system
In mathematics, the polar coordinate system is a two-dimensional coordinate system in which each point on a plane is determined by a distance from a fixed point and an angle from a fixed direction....
by
 then the arc length is given by
then the arc length is given by
In most cases, including even simple curves, there are no closed-form solutions of arc length and numerical integration
Numerical integration
In numerical analysis, numerical integration constitutes a broad family of algorithms for calculating the numerical value of a definite integral, and by extension, the term is also sometimes used to describe the numerical solution of differential equations. This article focuses on calculation of...
is necessary.
Curves with closed-form solution for arc length include the catenary
Catenary
In physics and geometry, the catenary is the curve that an idealised hanging chain or cable assumes when supported at its ends and acted on only by its own weight. The curve is the graph of the hyperbolic cosine function, and has a U-like shape, superficially similar in appearance to a parabola...
, circle
Circle
A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....
, cycloid
Cycloid
A cycloid is the curve traced by a point on the rim of a circular wheel as the wheel rolls along a straight line.It is an example of a roulette, a curve generated by a curve rolling on another curve....
, logarithmic spiral
Logarithmic spiral
A logarithmic spiral, equiangular spiral or growth spiral is a special kind of spiral curve which often appears in nature. The logarithmic spiral was first described by Descartes and later extensively investigated by Jacob Bernoulli, who called it Spira mirabilis, "the marvelous...
, parabola
Parabola
In mathematics, the parabola is a conic section, the intersection of a right circular conical surface and a plane parallel to a generating straight line of that surface...
, semicubical parabola and (mathematically, a curve) straight line
Line (mathematics)
The notion of line or straight line was introduced by the ancient mathematicians to represent straight objects with negligible width and depth. Lines are an idealization of such objects...
. The lack of closed form solution for the arc length of an elliptic arc led to the development of the elliptic integral
Elliptic integral
In integral calculus, elliptic integrals originally arose in connection with the problem of giving the arc length of an ellipse. They were first studied by Giulio Fagnano and Leonhard Euler...
s.
Derivation

Linear
In mathematics, a linear map or function f is a function which satisfies the following two properties:* Additivity : f = f + f...
segments. To make the value exact, and not an approximation
Approximation
An approximation is a representation of something that is not exact, but still close enough to be useful. Although approximation is most often applied to numbers, it is also frequently applied to such things as mathematical functions, shapes, and physical laws.Approximations may be used because...
, infinitely many linear elements are needed. This means that each element is infinitely small. This fact manifests itself later on when an integral
Integral
Integration is an important concept in mathematics and, together with its inverse, differentiation, is one of the two main operations in calculus...
is used.
Begin by looking at a representative linear segment (see image) and observe that its length (element of the arc length) will be the differential
Differential (mathematics)
In mathematics, the term differential has several meanings.-Basic notions:* In calculus, the differential represents a change in the linearization of a function....
ds. We will call the horizontal element of this distance dx, and the vertical element dy.
The Pythagorean theorem
Pythagorean theorem
In mathematics, the Pythagorean theorem or Pythagoras' theorem is a relation in Euclidean geometry among the three sides of a right triangle...
tells us that

Since the function is defined in time, segments (ds) are added up across infinitesimally small intervals of time (dt) yielding the integral

If y is a function of x, so that we could take t = x, then we have:

which is the arc length from x = a to x = b of the graph of the function ƒ.
For example, the curve in this figure is defined by

Subsequently, the arc length integral for values of t from -1 to 1 is

Using computational approximations, we can obtain a very accurate (but still approximate) arc length of 2.905. An expression in terms of the hypergeometric function can be obtained: it is
Another way to obtain the integral formula
Suppose that there exists a rectifiable curve given by a function f(x). To approximate the arc length S along f between two points a and b in that curve, construct a series of right triangles whose concatenated hypotenuses "cover" the arc of curve chosen as shown in the figure. For convenience, the bases of all those triangles can be set equal to , so that for each one an associated
, so that for each one an associated  exists. The length of any given hypotenuse is given by the Pythagorean Theorem
exists. The length of any given hypotenuse is given by the Pythagorean TheoremPythagorean theorem
In mathematics, the Pythagorean theorem or Pythagoras' theorem is a relation in Euclidean geometry among the three sides of a right triangle...
:
The summation of the lengths of the
 hypotenuses approximates
hypotenuses approximates  :
:Multiplying the radicand by
 produces:
produces:Then, our previous result becomes:
As the length
 of these segments decreases, the approximation improves. The limit of the approximation, as
of these segments decreases, the approximation improves. The limit of the approximation, as  goes to zero, is equal to
goes to zero, is equal to  :
:Another proof
We know that the formula for a line integral is . If we set the surface f(x,y) to 1, we will get arc length multiplied by 1, or
. If we set the surface f(x,y) to 1, we will get arc length multiplied by 1, or  . If x = t, and y = f(t), then y = f(x), from when x is a to when x is b. If we set these equations into our formula we get:
. If x = t, and y = f(t), then y = f(x), from when x is a to when x is b. If we set these equations into our formula we get:  (Note: If x = t then dt = dx). This is the arc length formula.
(Note: If x = t then dt = dx). This is the arc length formula.Arcs of circles
The length of an arc of a circleCircle
A circle is a simple shape of Euclidean geometry consisting of those points in a plane that are a given distance from a given point, the centre. The distance between any of the points and the centre is called the radius....
is the central angle divided by 360° multiplied by the circumference
Circumference
The circumference is the distance around a closed curve. Circumference is a special perimeter.-Circumference of a circle:The circumference of a circle is the length around it....
.
The circumference
Circumference
The circumference is the distance around a closed curve. Circumference is a special perimeter.-Circumference of a circle:The circumference of a circle is the length around it....
of a circle is
 , where r is the radius, or
, where r is the radius, or  , where d is the diameter.
, where d is the diameter.Arc lengths are denoted by s, since arcs "subtend" an angle.
If the angle measurement is in radians then
 where r is the radius and
where r is the radius and  is the subtended angle. The units of s will be the same as that of the radius.
is the subtended angle. The units of s will be the same as that of the radius.In a semicircle
Semicircle
In mathematics , a semicircle is a two-dimensional geometric shape that forms half of a circle. Being half of a circle's 360°, the arc of a semicircle always measures 180° or a half turn...
,
 .
.Ancient
For much of the history of mathematicsHistory of mathematics
The area of study known as the history of mathematics is primarily an investigation into the origin of discoveries in mathematics and, to a lesser extent, an investigation into the mathematical methods and notation of the past....
, even the greatest thinkers considered it impossible to compute the length of an irregular arc. Although Archimedes
Archimedes
Archimedes of Syracuse was a Greek mathematician, physicist, engineer, inventor, and astronomer. Although few details of his life are known, he is regarded as one of the leading scientists in classical antiquity. Among his advances in physics are the foundations of hydrostatics, statics and an...
had pioneered a way of finding the area beneath a curve with his method of exhaustion
Method of exhaustion
The method of exhaustion is a method of finding the area of a shape by inscribing inside it a sequence of polygons whose areas converge to the area of the containing shape. If the sequence is correctly constructed, the difference in area between the n-th polygon and the containing shape will...
, few believed it was even possible for curves to have definite lengths, as do straight lines. The first ground was broken in this field, as it often has been in calculus
Calculus
Calculus is a branch of mathematics focused on limits, functions, derivatives, integrals, and infinite series. This subject constitutes a major part of modern mathematics education. It has two major branches, differential calculus and integral calculus, which are related by the fundamental theorem...
, by approximation
Approximation
An approximation is a representation of something that is not exact, but still close enough to be useful. Although approximation is most often applied to numbers, it is also frequently applied to such things as mathematical functions, shapes, and physical laws.Approximations may be used because...
. People began to inscribe polygon
Polygon
In geometry a polygon is a flat shape consisting of straight lines that are joined to form a closed chain orcircuit.A polygon is traditionally a plane figure that is bounded by a closed path, composed of a finite sequence of straight line segments...
s within the curves and compute the length of the sides for a somewhat accurate measurement of the length. By using more segments, and by decreasing the length of each segment, they were able to obtain a more and more accurate approximation. In particular, by inscribing a polygon of many sides in a circle, they were able to find approximate values of π.
1600s
In the 17th century, the method of exhaustion led to the rectification by geometrical methods of several transcendental curveTranscendental curve
In mathematics, a transcendental curve is a curve that is not an algebraic curve. Here for a curve C what matters is the point set underlying C, not a given parametrisation...
s: the logarithmic spiral
Logarithmic spiral
A logarithmic spiral, equiangular spiral or growth spiral is a special kind of spiral curve which often appears in nature. The logarithmic spiral was first described by Descartes and later extensively investigated by Jacob Bernoulli, who called it Spira mirabilis, "the marvelous...
by Evangelista Torricelli
Evangelista Torricelli
Evangelista Torricelli was an Italian physicist and mathematician, best known for his invention of the barometer.-Biography:Evangelista Torricelli was born in Faenza, part of the Papal States...
in 1645 (some sources say John Wallis in the 1650s), the cycloid
Cycloid
A cycloid is the curve traced by a point on the rim of a circular wheel as the wheel rolls along a straight line.It is an example of a roulette, a curve generated by a curve rolling on another curve....
by Christopher Wren
Christopher Wren
Sir Christopher Wren FRS is one of the most highly acclaimed English architects in history.He used to be accorded responsibility for rebuilding 51 churches in the City of London after the Great Fire in 1666, including his masterpiece, St. Paul's Cathedral, on Ludgate Hill, completed in 1710...
in 1658, and the catenary
Catenary
In physics and geometry, the catenary is the curve that an idealised hanging chain or cable assumes when supported at its ends and acted on only by its own weight. The curve is the graph of the hyperbolic cosine function, and has a U-like shape, superficially similar in appearance to a parabola...
by Gottfried Leibniz
Gottfried Leibniz
Gottfried Wilhelm Leibniz was a German philosopher and mathematician. He wrote in different languages, primarily in Latin , French and German ....
in 1691.
In 1659, Wallis credited William Neile
William Neile
William Neile was an English mathematician and founder member of the Royal Society. His major mathematical work, the rectification of the semicubical parabola, was carried out when he was aged nineteen, and was published by John Wallis...
's discovery of the first rectification of a nontrivial algebraic curve
Algebraic curve
In algebraic geometry, an algebraic curve is an algebraic variety of dimension one. The theory of these curves in general was quite fully developed in the nineteenth century, after many particular examples had been considered, starting with circles and other conic sections.- Plane algebraic curves...
, the semicubical parabola.
Integral form
Before the full formal development of the calculus, the basis for the modern integral form for arc length was independently discovered by Hendrik van HeuraetHendrik van Heuraet
Hendrik van Heuraet was a Dutch mathematician. He was noted as one of the founders of the integral. From [1653 he studied at Leiden University where he interacted with Frans van Schooten, Johannes Hudde, and Christiaan Huygens. In 1658 he and Hudde left for Saumur in France. He returned to Leiden...
and Pierre de Fermat
Pierre de Fermat
Pierre de Fermat was a French lawyer at the Parlement of Toulouse, France, and an amateur mathematician who is given credit for early developments that led to infinitesimal calculus, including his adequality...
.
In 1659 van Heuraet published a construction showing that arc length could be interpreted as the area under a curve—this integral, in effect—and applied it to the parabola
Parabola
In mathematics, the parabola is a conic section, the intersection of a right circular conical surface and a plane parallel to a generating straight line of that surface...
. In 1660, Fermat published a more general theory containing the same result in his De linearum curvarum cum lineis rectis comparatione dissertatio geometrica.


whose tangent
Tangent
In geometry, the tangent line to a plane curve at a given point is the straight line that "just touches" the curve at that point. More precisely, a straight line is said to be a tangent of a curve at a point on the curve if the line passes through the point on the curve and has slope where f...
at x = a had a slope
Slope
In mathematics, the slope or gradient of a line describes its steepness, incline, or grade. A higher slope value indicates a steeper incline....
of

so the tangent line would have the equation

Next, he increased a by a small amount to a + ε, making segment AC a relatively good approximation for the length of the curve from A to D. To find the length of the segment AC, he used the Pythagorean theorem
Pythagorean theorem
In mathematics, the Pythagorean theorem or Pythagoras' theorem is a relation in Euclidean geometry among the three sides of a right triangle...
:
-

which, when solved, yields

In order to approximate the length, Fermat would sum up a sequence of short segments.
Curves with infinite length
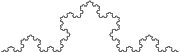 As mentioned above, some curves are non-rectifiable, that is, there is no upper bound on the lengths of polygonal approximations; the length can be made arbitrarily large. Informally, such curves are said to have infinite length. There are continuous curves on which every arc (other than a single-point arc) has infinite length. An example of such a curve is the Koch curve
As mentioned above, some curves are non-rectifiable, that is, there is no upper bound on the lengths of polygonal approximations; the length can be made arbitrarily large. Informally, such curves are said to have infinite length. There are continuous curves on which every arc (other than a single-point arc) has infinite length. An example of such a curve is the Koch curve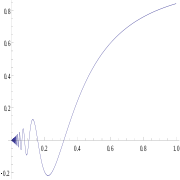 Koch snowflakeThe Koch snowflake is a mathematical curve and one of the earliest fractal curves to have been described...
Koch snowflakeThe Koch snowflake is a mathematical curve and one of the earliest fractal curves to have been described...
. Another example of a curve with infinite length is the graph of the function defined by f(x) = x sin(1/x) for any open set with 0 as one of its delimiters and f(0) = 0. Sometimes the Hausdorff dimensionHausdorff dimensionthumb|450px|Estimating the Hausdorff dimension of the coast of Great BritainIn mathematics, the Hausdorff dimension is an extended non-negative real number associated with any metric space. The Hausdorff dimension generalizes the notion of the dimension of a real vector space...
and Hausdorff measureHausdorff measureIn mathematics a Hausdorff measure is a type of outer measure, named for Felix Hausdorff, that assigns a number in [0,∞] to each set in Rn or, more generally, in any metric space. The zero dimensional Hausdorff measure is the number of points in the set or ∞ if the set is infinite...
are used to "measure" the size of infinite-length curves.
Generalization to (pseudo-)Riemannian manifolds
Let M be a (pseudo-)Riemannian manifoldPseudo-Riemannian manifoldIn differential geometry, a pseudo-Riemannian manifold is a generalization of a Riemannian manifold. It is one of many mathematical objects named after Bernhard Riemann. The key difference between a Riemannian manifold and a pseudo-Riemannian manifold is that on a pseudo-Riemannian manifold the...
, γ : [0, 1] → M a curve in M and g the (pseudo-) metric tensor.
The length of γ is defined to be

where γ'(t) ∈ Tγ(t)M is the tangent vector of γ at t. The sign in the square root is chosen once for a given curve, to ensure that the square root is a real number. The positive sign is chosen for spacelike curves; in a pseudo-Riemannian manifold, the negative sign may be chosen for timelike curves.
In theory of relativityTheory of relativityThe theory of relativity, or simply relativity, encompasses two theories of Albert Einstein: special relativity and general relativity. However, the word relativity is sometimes used in reference to Galilean invariance....
, arc-length of timelike curves (world lineWorld lineIn physics, the world line of an object is the unique path of that object as it travels through 4-dimensional spacetime. The concept of "world line" is distinguished from the concept of "orbit" or "trajectory" by the time dimension, and typically encompasses a large area of spacetime wherein...
s) is the proper timeProper timeIn relativity, proper time is the elapsed time between two events as measured by a clock that passes through both events. The proper time depends not only on the events but also on the motion of the clock between the events. An accelerated clock will measure a smaller elapsed time between two...
elapsed along the world line.
See also
- Arc (geometry)Arc (geometry)In geometry, an arc is a closed segment of a differentiable curve in the two-dimensional plane; for example, a circular arc is a segment of the circumference of a circle...
- Integral approximationsNumerical integrationIn numerical analysis, numerical integration constitutes a broad family of algorithms for calculating the numerical value of a definite integral, and by extension, the term is also sometimes used to describe the numerical solution of differential equations. This article focuses on calculation of...
- GeodesicGeodesicIn mathematics, a geodesic is a generalization of the notion of a "straight line" to "curved spaces". In the presence of a Riemannian metric, geodesics are defined to be the shortest path between points in the space...
s - Meridian arcMeridian arcIn geodesy, a meridian arc measurement is a highly accurate determination of the distance between two points with the same longitude. Two or more such determinations at different locations then specify the shape of the reference ellipsoid which best approximates the shape of the geoid. This...
External links
- Math Before Calculus
- The History of Curvature
- Arc Length by Ed Pegg, Jr.Ed Pegg, Jr.Ed Pegg, Jr. is an expert on mathematical puzzles and is a self-described recreational mathematician. He creates puzzles for the Mathematical Association of America online at Ed Pegg, Jr.'s Math Games. His puzzles have also been used by Will Shortz on the puzzle segment of NPR's Weekend Edition...
, The Wolfram Demonstrations Project, 2007. - Calculus Study Guide – Arc Length (Rectification)
- Famous Curves Index The MacTutor History of Mathematics archive
- Arc Length Approximation by Chad Pierson, Josh Fritz, and Angela Sharp, The Wolfram Demonstrations Project.
- Length of a Curve Experiment Illustrates numerical solution of finding length of a curve.
- Arc (geometry)







