
Non-linear least squares
Encyclopedia
Non-linear least squares is the form of least squares
analysis which is used to fit a set of m observations with a model that is non-linear in n unknown parameters (m > n). It is used in some forms of non-linear regression. The basis of the method is to approximate the model by a linear one and to refine the parameters by successive iterations. There are many similarities to linear least squares
, but also some significant differences.
 data points,
data points, 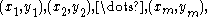 and a curve (model function)
and a curve (model function) 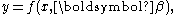 that in addition to the variable
that in addition to the variable  also depends on
also depends on  parameters,
parameters,  with
with  It is desired to find the vector
It is desired to find the vector 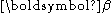 of parameters such that the curve fits best the given data in the least squares sense, that is, the sum of squares
of parameters such that the curve fits best the given data in the least squares sense, that is, the sum of squares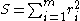
is minimized, where the residuals
(errors) ri are given by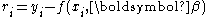
for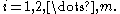
The minimum
value of S occurs when the gradient
is zero. Since the model contains n parameters there are n gradient equations:
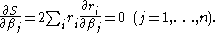
In a non-linear system, the derivatives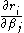 are functions of both the independent variable and the parameters, so these gradient equations do not have a closed solution. Instead, initial values must be chosen for the parameters. Then, the parameters are refined iteratively, that is, the values are obtained by successive approximation,
are functions of both the independent variable and the parameters, so these gradient equations do not have a closed solution. Instead, initial values must be chosen for the parameters. Then, the parameters are refined iteratively, that is, the values are obtained by successive approximation,
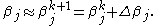
Here, k is an iteration number and the vector of increments,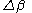 is known as the shift vector. At each iteration the model is linearized by approximation to a first-order Taylor series
is known as the shift vector. At each iteration the model is linearized by approximation to a first-order Taylor series
expansion about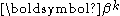
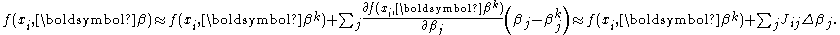
The Jacobian
, J, is a function of constants, the independent variable and the parameters, so it changes from one iteration to the next. Thus, in terms of the linearized model,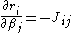 and the residuals are given by
and the residuals are given by
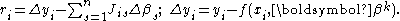
Substituting these expressions into the gradient equations, they become
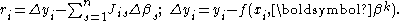
which, on rearrangement, become n simultaneous linear equations, the normal equations
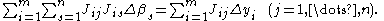
The normal equations are written in matrix notation as
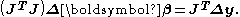
When the observations are not equally reliable, a weighted sum of squares may be minimized,

Each element of the diagonal
weight matrix, W should, ideally, be equal to the reciprocal of the variance
of the measurement.
The normal equations are then

These equations form the basis for the Gauss-Newton algorithm
for a non-linear least squares problem.
, S, is a quadratic function of the parameters.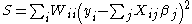
When there is only one parameter the graph of S with respect to that parameter will be a parabola
. With two or more parameters the contours of S with respect to any pair of parameters will be concentric ellipse
s (assuming that the normal equations matrix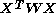 is positive definite). The minimum parameter values are to be found at the centre of the ellipses. The geometry of the general objective function can be described as paraboloid elliptical.
is positive definite). The minimum parameter values are to be found at the centre of the ellipses. The geometry of the general objective function can be described as paraboloid elliptical.
In NLLSQ the objective function is quadratic with respect to the parameters only in a region close to its minimum value, where the truncated Taylor series is a good approximation to the model.
The more the parameter values differ from their optimal values, the more the contours deviate from elliptical shape. A consequence of this is that initial parameter estimates should be as close as practicable to their (unknown!) optimal values. It also explains how divergence can come about as the Gauss-Newton algorithm is convergent only when the objective function is approximately quadratic in the parameters.
. Both the observed and calculated data are displayed on a screen. The parameters of the model are adjusted by hand until the agreement between observed and calculated data is reasonably good. Although this will be a subjective judgment, it is sufficient to find a good starting point for the non-linear refinement.
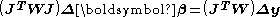
may be solved for by Cholesky decomposition
by Cholesky decomposition
, as described in linear least squares. The parameters are updated iteratively
where k is an iteration number. While this method may be adequate for simple models, it will fail if divergence occurs. Therefore protection against divergence is essential.
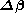 , by a fraction, f
, by a fraction, f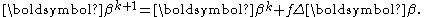
For example the length of the shift vector may be successively halved until the new value of the objective function is less than its value at the last iteration. The fraction, f could be optimized by a line search. As each trial value of f requires the objective function to be re-calculated it is not worth optimizing its value too stringently.
When using shift-cutting, the direction of the shift vector remains unchanged. This limits the applicability of the method to situations where the direction of the shift vector is not very different from what it would be if the objective function were approximately quadratic in the parameters,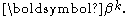

where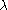 is the Marquardt parameter and I is an identity matrix. Increasing the value of
is the Marquardt parameter and I is an identity matrix. Increasing the value of 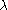 has the effect of changing both the direction and the length of the shift vector. The shift vector is rotated towards the direction of steepest descent
has the effect of changing both the direction and the length of the shift vector. The shift vector is rotated towards the direction of steepest descent
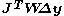 is the steepest descent vector. So, when
is the steepest descent vector. So, when 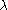 becomes very large, the shift vector becomes a small fraction of the steepest descent vector.
becomes very large, the shift vector becomes a small fraction of the steepest descent vector.
Various strategies have been proposed for the determination of the Marquardt parameter. As with shift-cutting, it is wasteful to optimize this parameter too stringently. Rather, once a value has been found that brings about a reduction in the value of the objective function, that value of the parameter is carried to the next iteration, reduced if possible, or increased if need be. When reducing the value of the Marquardt parameter, there is a cut-off value below which it is safe to set it to zero, that is, to continue with the unmodified Gauss-Newton method. The cut-off value may be set equal to the smallest singular value of the Jacobian. A bound for this value is given by .
.

The Jacobian is subjected to an orthogonal decomposition; the QR decomposition
will serve to illustrate the process.
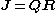
where Q is an orthogonal
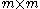 matrix and R is an
matrix and R is an 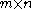 matrix which is partitioned
matrix which is partitioned
into a block,
block, 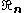 , and a
, and a 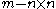 zero block.
zero block. 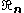 is upper triangular.
is upper triangular.

The residual vector is left-multiplied by .
.
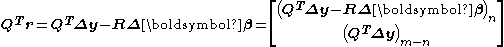
This has no effect on the sum of squares since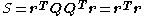 because Q is orthogonal
because Q is orthogonal
The minimum value of S is attained when the upper block is zero. Therefore the shift vector is found by solving
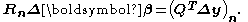
These equations are easily solved as R is upper triangular.
, in which R is diagonalized by further orthogonal transformations.
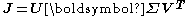
where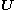 is orthogonal,
is orthogonal, 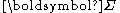 is a diagonal matrix of singular values and
is a diagonal matrix of singular values and 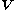 is the orthogonal matrix of the eigenvectors of
is the orthogonal matrix of the eigenvectors of 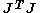 or equivalently the right singular vectors of
or equivalently the right singular vectors of 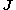 . In this case the shift vector is given by
. In this case the shift vector is given by
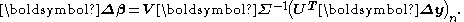
The relative simplicity of this expression is very useful in theoretical analysis of non-linear least squares. The application of singular value decomposition is discussed in detail in Lawson and Hanson.

The value 0.0001 is somewhat arbitrary and may need to changed. In particular it may need to be increased when experimental errors are large. An alternative criterion is
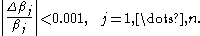
Again, the numerical value is somewhat arbitrary; 0.001 is equivalent to specifying that each parameter should be refined to 0.1% precision. This is reasonable when it is less than the largest relative standard deviation on the parameters.
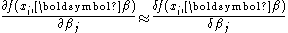
is obtained by calculation of for
for 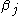 and
and 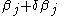 . The increment,
. The increment,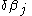 , size should be chosen so the numerical derivative is not subject to approximation error by being too large, or round-off error by being too small.
, size should be chosen so the numerical derivative is not subject to approximation error by being too large, or round-off error by being too small.
where is the height,
is the height,  is the position and
is the position and 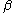 is the half-width at half height, there are two solutions for the half-width,
is the half-width at half height, there are two solutions for the half-width, 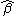 and
and 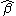 which give the same optimal value for the objective function.
which give the same optimal value for the objective function.
Not all multiple minima have equal values of the objective function. False minima, also known as local minima, occur when the objective function value is greater than its value at the so-called global minimum. To be certain that the minimum found is the global minimum, the refinement should be started with widely differing initial values of the parameters. When the same minimum is found regardless of starting point, it is likely to be the global minimum.
When multiple minima exist there is an important consequence: the objective function will have a maximum value somewhere between two minima. The normal equations matrix is not positive definite at a maximum in the objective function, as the gradient is zero and no unique direction of descent exists. Refinement from a point (a set of parameter values) close to a maximum will be ill-conditioned and should be avoided as a starting point. For example, when fitting a Lorentzian the normal equations matrix is not positive definite when the half-width of the band is zero.
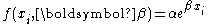
it can be transformed into a linear model by taking logarithms.
The sum of squares becomes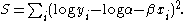
This procedure should be avoided unless the errors are multiplicative and log-normally distributed because it can give misleading results. This comes from the fact that whatever the experimental errors on y might be, the errors on log y are different. Therefore, when the transformed sum of squares is minimized different results will be obtained both for the parameter values and their calculated standard deviations. However, with multiplicative errors that are log-normally distributed, this procedure gives unbiased and consistent parameter estimates.
Another example is furnished by Michaelis–Menten kinetics, used to determine two parameters .
.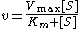
The Lineweaver–Burk plot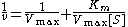
of 1/v against [S] is very sensitive to data error and it is strongly biased toward fitting the data in a particular range of the independent variable, [S].
The matrix H is known as the Hessian matrix
. Although this model has better convergence properties near to the minimum, it is much worse when the parameters are far from their optimal values. Calculation of the Hessian adds to the complexity of the algorithm. This method is not in general use.
More detailed descriptions of these, and other, methods are available, in Numerical Recipes
, together with computer code in various languages.
Least squares
The method of least squares is a standard approach to the approximate solution of overdetermined systems, i.e., sets of equations in which there are more equations than unknowns. "Least squares" means that the overall solution minimizes the sum of the squares of the errors made in solving every...
analysis which is used to fit a set of m observations with a model that is non-linear in n unknown parameters (m > n). It is used in some forms of non-linear regression. The basis of the method is to approximate the model by a linear one and to refine the parameters by successive iterations. There are many similarities to linear least squares
Linear least squares
In statistics and mathematics, linear least squares is an approach to fitting a mathematical or statistical model to data in cases where the idealized value provided by the model for any data point is expressed linearly in terms of the unknown parameters of the model...
, but also some significant differences.
Theory
Consider a set of data points,
data points, 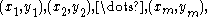 and a curve (model function)
and a curve (model function) 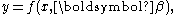 that in addition to the variable
that in addition to the variable  also depends on
also depends on  parameters,
parameters,  with
with  It is desired to find the vector
It is desired to find the vector 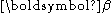 of parameters such that the curve fits best the given data in the least squares sense, that is, the sum of squares
of parameters such that the curve fits best the given data in the least squares sense, that is, the sum of squares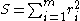
is minimized, where the residuals
Errors and residuals in statistics
In statistics and optimization, statistical errors and residuals are two closely related and easily confused measures of the deviation of a sample from its "theoretical value"...
(errors) ri are given by
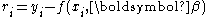
for
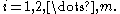
The minimum
Maxima and minima
In mathematics, the maximum and minimum of a function, known collectively as extrema , are the largest and smallest value that the function takes at a point either within a given neighborhood or on the function domain in its entirety .More generally, the...
value of S occurs when the gradient
Gradient
In vector calculus, the gradient of a scalar field is a vector field that points in the direction of the greatest rate of increase of the scalar field, and whose magnitude is the greatest rate of change....
is zero. Since the model contains n parameters there are n gradient equations:
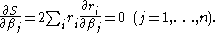
In a non-linear system, the derivatives
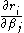 are functions of both the independent variable and the parameters, so these gradient equations do not have a closed solution. Instead, initial values must be chosen for the parameters. Then, the parameters are refined iteratively, that is, the values are obtained by successive approximation,
are functions of both the independent variable and the parameters, so these gradient equations do not have a closed solution. Instead, initial values must be chosen for the parameters. Then, the parameters are refined iteratively, that is, the values are obtained by successive approximation,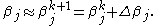
Here, k is an iteration number and the vector of increments,
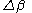 is known as the shift vector. At each iteration the model is linearized by approximation to a first-order Taylor series
is known as the shift vector. At each iteration the model is linearized by approximation to a first-order Taylor seriesTaylor series
In mathematics, a Taylor series is a representation of a function as an infinite sum of terms that are calculated from the values of the function's derivatives at a single point....
expansion about
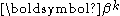
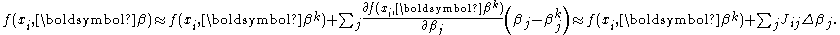
The Jacobian
Jacobian
In vector calculus, the Jacobian matrix is the matrix of all first-order partial derivatives of a vector- or scalar-valued function with respect to another vector. Suppose F : Rn → Rm is a function from Euclidean n-space to Euclidean m-space...
, J, is a function of constants, the independent variable and the parameters, so it changes from one iteration to the next. Thus, in terms of the linearized model,
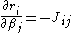 and the residuals are given by
and the residuals are given by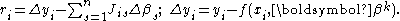
Substituting these expressions into the gradient equations, they become
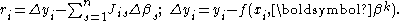
which, on rearrangement, become n simultaneous linear equations, the normal equations
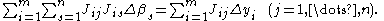
The normal equations are written in matrix notation as
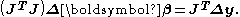
When the observations are not equally reliable, a weighted sum of squares may be minimized,

Each element of the diagonal
Diagonal
A diagonal is a line joining two nonconsecutive vertices of a polygon or polyhedron. Informally, any sloping line is called diagonal. The word "diagonal" derives from the Greek διαγώνιος , from dia- and gonia ; it was used by both Strabo and Euclid to refer to a line connecting two vertices of a...
weight matrix, W should, ideally, be equal to the reciprocal of the variance
Variance
In probability theory and statistics, the variance is a measure of how far a set of numbers is spread out. It is one of several descriptors of a probability distribution, describing how far the numbers lie from the mean . In particular, the variance is one of the moments of a distribution...
of the measurement.
The normal equations are then

These equations form the basis for the Gauss-Newton algorithm
Gauss-Newton algorithm
The Gauss–Newton algorithm is a method used to solve non-linear least squares problems. It can be seen as a modification of Newton's method for finding a minimum of a function...
for a non-linear least squares problem.
Geometrical interpretation
In linear least squares the objective functionOptimization (mathematics)
In mathematics, computational science, or management science, mathematical optimization refers to the selection of a best element from some set of available alternatives....
, S, is a quadratic function of the parameters.
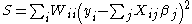
When there is only one parameter the graph of S with respect to that parameter will be a parabola
Parabola
In mathematics, the parabola is a conic section, the intersection of a right circular conical surface and a plane parallel to a generating straight line of that surface...
. With two or more parameters the contours of S with respect to any pair of parameters will be concentric ellipse
Ellipse
In geometry, an ellipse is a plane curve that results from the intersection of a cone by a plane in a way that produces a closed curve. Circles are special cases of ellipses, obtained when the cutting plane is orthogonal to the cone's axis...
s (assuming that the normal equations matrix
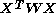 is positive definite). The minimum parameter values are to be found at the centre of the ellipses. The geometry of the general objective function can be described as paraboloid elliptical.
is positive definite). The minimum parameter values are to be found at the centre of the ellipses. The geometry of the general objective function can be described as paraboloid elliptical.In NLLSQ the objective function is quadratic with respect to the parameters only in a region close to its minimum value, where the truncated Taylor series is a good approximation to the model.

The more the parameter values differ from their optimal values, the more the contours deviate from elliptical shape. A consequence of this is that initial parameter estimates should be as close as practicable to their (unknown!) optimal values. It also explains how divergence can come about as the Gauss-Newton algorithm is convergent only when the objective function is approximately quadratic in the parameters.
Initial parameter estimates
Problems of ill-conditioning and divergence can be ameliorated by finding initial parameter estimates that are near to the optimal values. A good way to do this is by computer simulationComputer simulation
A computer simulation, a computer model, or a computational model is a computer program, or network of computers, that attempts to simulate an abstract model of a particular system...
. Both the observed and calculated data are displayed on a screen. The parameters of the model are adjusted by hand until the agreement between observed and calculated data is reasonably good. Although this will be a subjective judgment, it is sufficient to find a good starting point for the non-linear refinement.
Gauss–Newton method
The normal equations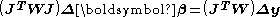
may be solved for
 by Cholesky decomposition
by Cholesky decompositionCholesky decomposition
In linear algebra, the Cholesky decomposition or Cholesky triangle is a decomposition of a Hermitian, positive-definite matrix into the product of a lower triangular matrix and its conjugate transpose. It was discovered by André-Louis Cholesky for real matrices...
, as described in linear least squares. The parameters are updated iteratively

where k is an iteration number. While this method may be adequate for simple models, it will fail if divergence occurs. Therefore protection against divergence is essential.
Shift-cutting
If divergence occurs, a simple expedient is to reduce the length of the shift vector,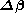 , by a fraction, f
, by a fraction, f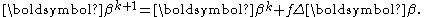
For example the length of the shift vector may be successively halved until the new value of the objective function is less than its value at the last iteration. The fraction, f could be optimized by a line search. As each trial value of f requires the objective function to be re-calculated it is not worth optimizing its value too stringently.
When using shift-cutting, the direction of the shift vector remains unchanged. This limits the applicability of the method to situations where the direction of the shift vector is not very different from what it would be if the objective function were approximately quadratic in the parameters,
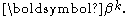
Marquardt parameter
If divergence occurs and the direction of the shift vector is so far from its "ideal" direction that shift-cutting is not very effective, that is, the fraction, f required to avoid divergence is very small, the direction must be changed. This can achieved by using the Marquardt parameter. In this method the normal equations are modified
where
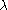 is the Marquardt parameter and I is an identity matrix. Increasing the value of
is the Marquardt parameter and I is an identity matrix. Increasing the value of 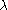 has the effect of changing both the direction and the length of the shift vector. The shift vector is rotated towards the direction of steepest descent
has the effect of changing both the direction and the length of the shift vector. The shift vector is rotated towards the direction of steepest descent
- when

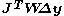 is the steepest descent vector. So, when
is the steepest descent vector. So, when 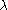 becomes very large, the shift vector becomes a small fraction of the steepest descent vector.
becomes very large, the shift vector becomes a small fraction of the steepest descent vector.Various strategies have been proposed for the determination of the Marquardt parameter. As with shift-cutting, it is wasteful to optimize this parameter too stringently. Rather, once a value has been found that brings about a reduction in the value of the objective function, that value of the parameter is carried to the next iteration, reduced if possible, or increased if need be. When reducing the value of the Marquardt parameter, there is a cut-off value below which it is safe to set it to zero, that is, to continue with the unmodified Gauss-Newton method. The cut-off value may be set equal to the smallest singular value of the Jacobian. A bound for this value is given by
 .
.QR decomposition
The minimum in the sum of squares can be found by a method that does not involve forming the normal equations. The residuals with the linearized model can be written as
The Jacobian is subjected to an orthogonal decomposition; the QR decomposition
QR decomposition
In linear algebra, a QR decomposition of a matrix is a decomposition of a matrix A into a product A=QR of an orthogonal matrix Q and an upper triangular matrix R...
will serve to illustrate the process.
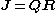
where Q is an orthogonal
Orthogonal matrix
In linear algebra, an orthogonal matrix , is a square matrix with real entries whose columns and rows are orthogonal unit vectors ....
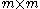 matrix and R is an
matrix and R is an 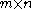 matrix which is partitioned
matrix which is partitionedBlock matrix
In the mathematical discipline of matrix theory, a block matrix or a partitioned matrix is a matrix broken into sections called blocks. Looking at it another way, the matrix is written in terms of smaller matrices. We group the rows and columns into adjacent 'bunches'. A partition is the rectangle...
into a
 block,
block, 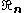 , and a
, and a 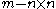 zero block.
zero block. 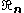 is upper triangular.
is upper triangular.
The residual vector is left-multiplied by
 .
.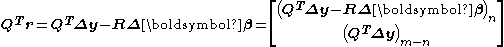
This has no effect on the sum of squares since
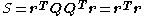 because Q is orthogonal
because Q is orthogonalThe minimum value of S is attained when the upper block is zero. Therefore the shift vector is found by solving
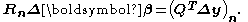
These equations are easily solved as R is upper triangular.
Singular value decomposition
A variant of the method of orthogonal decomposition involves singular value decompositionSingular value decomposition
In linear algebra, the singular value decomposition is a factorization of a real or complex matrix, with many useful applications in signal processing and statistics....
, in which R is diagonalized by further orthogonal transformations.
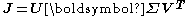
where
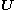 is orthogonal,
is orthogonal, 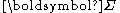 is a diagonal matrix of singular values and
is a diagonal matrix of singular values and 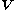 is the orthogonal matrix of the eigenvectors of
is the orthogonal matrix of the eigenvectors of 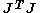 or equivalently the right singular vectors of
or equivalently the right singular vectors of 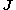 . In this case the shift vector is given by
. In this case the shift vector is given by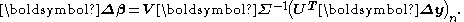
The relative simplicity of this expression is very useful in theoretical analysis of non-linear least squares. The application of singular value decomposition is discussed in detail in Lawson and Hanson.
Convergence criteria
The common sense criterion for convergence is that the sum of squares does not decrease from one iteration to the next. However this criterion is often difficult to implement in practice, for various reasons. A useful convergence criterion is
The value 0.0001 is somewhat arbitrary and may need to changed. In particular it may need to be increased when experimental errors are large. An alternative criterion is
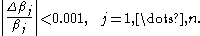
Again, the numerical value is somewhat arbitrary; 0.001 is equivalent to specifying that each parameter should be refined to 0.1% precision. This is reasonable when it is less than the largest relative standard deviation on the parameters.
Calculation of the Jacobian by numerical approximation
There are models for which it is either very difficult or even impossible to derive analytical expressions for the elements of the Jacobian. Then, the numerical approximation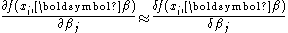
is obtained by calculation of
 for
for 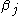 and
and 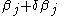 . The increment,
. The increment,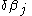 , size should be chosen so the numerical derivative is not subject to approximation error by being too large, or round-off error by being too small.
, size should be chosen so the numerical derivative is not subject to approximation error by being too large, or round-off error by being too small.Parameter errors, confidence limits, residuals etc.
For details concerning these topics see linear least squares#Parameter errors, correlation and confidence limitsMultiple minima
Multiple minima can occur in a variety of circumstances some of which are:- A parameter is raised to a power of two or more. For example, when fitting data to a LorentzianLorentzianLorentzian may refer to* Cauchy–Lorentz distribution, also known as the Lorentz distribution, Lorentzian function, or Cauchy distribution* Lorentz transformation* Lorentzian inner product* Lorentzian manifoldThe name Lorentz may refer to*Hendrik Lorentz...
curve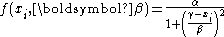
where
 is the height,
is the height,  is the position and
is the position and 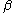 is the half-width at half height, there are two solutions for the half-width,
is the half-width at half height, there are two solutions for the half-width, 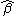 and
and 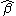 which give the same optimal value for the objective function.
which give the same optimal value for the objective function.
- Two parameters can be interchanged without changing the value of the model. A simple example is when the model contains the product of two parameters, since
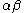 will give the same value as
will give the same value as 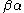 .
. - A parameter is in a trigonometric function, such as
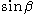 , which has identical values at
, which has identical values at 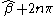 . See Levenberg–Marquardt algorithm for an example.
. See Levenberg–Marquardt algorithm for an example.
Not all multiple minima have equal values of the objective function. False minima, also known as local minima, occur when the objective function value is greater than its value at the so-called global minimum. To be certain that the minimum found is the global minimum, the refinement should be started with widely differing initial values of the parameters. When the same minimum is found regardless of starting point, it is likely to be the global minimum.
When multiple minima exist there is an important consequence: the objective function will have a maximum value somewhere between two minima. The normal equations matrix is not positive definite at a maximum in the objective function, as the gradient is zero and no unique direction of descent exists. Refinement from a point (a set of parameter values) close to a maximum will be ill-conditioned and should be avoided as a starting point. For example, when fitting a Lorentzian the normal equations matrix is not positive definite when the half-width of the band is zero.
Transformation to a linear model
A non-linear model can sometimes be transformed into a linear one. For example, when the model is a simple exponential function,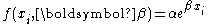
it can be transformed into a linear model by taking logarithms.

The sum of squares becomes
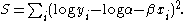
This procedure should be avoided unless the errors are multiplicative and log-normally distributed because it can give misleading results. This comes from the fact that whatever the experimental errors on y might be, the errors on log y are different. Therefore, when the transformed sum of squares is minimized different results will be obtained both for the parameter values and their calculated standard deviations. However, with multiplicative errors that are log-normally distributed, this procedure gives unbiased and consistent parameter estimates.
Another example is furnished by Michaelis–Menten kinetics, used to determine two parameters
 .
.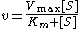
The Lineweaver–Burk plot
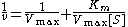
of 1/v against [S] is very sensitive to data error and it is strongly biased toward fitting the data in a particular range of the independent variable, [S].
Gradient methods
There are many examples in the scientific literature where different methods have been used for non-linear data-fitting problems.- Inclusion of second derivatives in The Taylor series expansion of the model function. This is Newton's method in optimizationNewton's method in optimizationIn mathematics, Newton's method is an iterative method for finding roots of equations. More generally, Newton's method is used to find critical points of differentiable functions, which are the zeros of the derivative function.-Method:...
.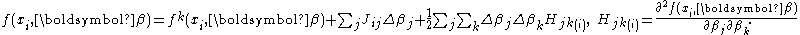
The matrix H is known as the Hessian matrix
Hessian matrix
In mathematics, the Hessian matrix is the square matrix of second-order partial derivatives of a function; that is, it describes the local curvature of a function of many variables. The Hessian matrix was developed in the 19th century by the German mathematician Ludwig Otto Hesse and later named...
. Although this model has better convergence properties near to the minimum, it is much worse when the parameters are far from their optimal values. Calculation of the Hessian adds to the complexity of the algorithm. This method is not in general use.
- Davidon-Fletcher-Powell methodDavidon-Fletcher-Powell formulaThe Davidon–Fletcher–Powell formula finds the solution to the secant equation that is closest to the current estimate and satisfies the curvature condition . It was the first quasi-Newton method which generalize the secant method to a multidimensional problem...
. This method, a form of pseudo-Newton method, is similar to the one above but calculates the Hessian by successive approximation, to avoid having to use analytical expressions for the second derivatives. - Steepest descent. Although a reduction in the sum of squares is guaranteed when the shift vector points in the direction of steepest descent, this method often performs poorly. When the parameter values are far from optimal the direction of the steepest descent vector, which is normal (perpendicular) to the contours of the objective function, is very different from the direction of the Gauss-Newton vector. This makes divergence much more likely, especially as the minimum along the direction of steepest descent may correspond to a small fraction of the length of the steepest descent vector. When the contours of the objective function are very eccentric, due to there being high correlation between parameters. the steepest descent iterations, with shift-cutting, follow a slow, zig-zag trajectory towards the minimum.
- Conjugate gradient searchConjugate gradient methodIn mathematics, the conjugate gradient method is an algorithm for the numerical solution of particular systems of linear equations, namely those whose matrix is symmetric and positive-definite. The conjugate gradient method is an iterative method, so it can be applied to sparse systems that are too...
. This is an improved steepest descent based method with good theoretical convergence properties, although it can fail on finite-precision digital computers even when used on quadratic problems.
Direct search methods
Direct search methods depend on evaluations of the objective function at a variety of parameter values and do not use derivatives at all. They offer alternatives to the use of numerical derivatives in the Gauss-Newton method and gradient methods.- Alternating variable search. Each parameter is varied in turn by adding a fixed or variable increment to it and retaining the value that brings about a reduction in the sum of squares. The method is simple and effective when the parameters are not highly correlated. It has very poor convergence properties, but may be useful for finding initial parameter estimates.
- Nelder-Mead (Simplex) searchNelder-Mead methodThe Nelder–Mead method or downhill simplex method or amoeba method is a commonly used nonlinear optimization technique, which is a well-defined numerical method for twice differentiable and unimodal problems...
A simplexSimplexIn geometry, a simplex is a generalization of the notion of a triangle or tetrahedron to arbitrary dimension. Specifically, an n-simplex is an n-dimensional polytope which is the convex hull of its n + 1 vertices. For example, a 2-simplex is a triangle, a 3-simplex is a tetrahedron,...
in this context is a polytopePolytopeIn elementary geometry, a polytope is a geometric object with flat sides, which exists in any general number of dimensions. A polygon is a polytope in two dimensions, a polyhedron in three dimensions, and so on in higher dimensions...
of n + 1 vertices in n dimensions; a triangle on a plane, a tetrahedron in three-dimensional space and so forth. Each vertex corresponds to a value of the objective function for a particular set of parameters. The shape and size of the simplex is adjusted by varying the parameters in such a way that the value of the objective function at the highest vertex always decreases. Although the sum of squares may initially decrease rapidly, it can converge to a nonstationary point on quasiconvex problems, by an example of M. J. D. Powell.
More detailed descriptions of these, and other, methods are available, in Numerical Recipes
Numerical Recipes
Numerical Recipes is the generic title of a series of books on algorithms and numerical analysis by William H. Press, Saul Teukolsky, William Vetterling and Brian Flannery. In various editions, the books have been in print since 1986...
, together with computer code in various languages.
See also
- Least squares support vector machineLeast squares support vector machineLeast squares support vector machines are least squares versions of support vector machines , which are a set of related supervised learning methods that analyze data and recognize patterns, and which are used for classification and regression analysis...
- Curve fittingCurve fittingCurve fitting is the process of constructing a curve, or mathematical function, that has the best fit to a series of data points, possibly subject to constraints. Curve fitting can involve either interpolation, where an exact fit to the data is required, or smoothing, in which a "smooth" function...
- Nonlinear programmingNonlinear programmingIn mathematics, nonlinear programming is the process of solving a system of equalities and inequalities, collectively termed constraints, over a set of unknown real variables, along with an objective function to be maximized or minimized, where some of the constraints or the objective function are...
- Optimization (mathematics)Optimization (mathematics)In mathematics, computational science, or management science, mathematical optimization refers to the selection of a best element from some set of available alternatives....
- Levenberg–Marquardt algorithm

