
Center of gravity
Encyclopedia
In physics
, a center of gravity of a material body is a point that may be used for a summary description of gravitational interactions. In a uniform gravitational field, the center of mass
serves as the center of gravity. This is a very good approximation for smaller bodies near the surface of Earth, so there is no practical need to distinguish "center of gravity" from "center of mass" in most applications, such as engineering and medicine.
In a non-uniform field, gravitational effects such as potential energy
, force
, and torque
can no longer be calculated using the center of mass alone. In particular, a non-uniform gravitational field can produce a torque on an object, causing it to rotate. The center of gravity seeks to explain this effect. Formally, a center of gravity is an application point of the resultant gravitational force on the body. Such a point may not exist, and if it exists, it is not unique. One can further define a unique center of gravity by approximating the field as either parallel or spherically symmetric.
The concept of a center of gravity as distinct from the center of mass is rarely used in applications, even in celestial mechanics
, where non-uniform fields are important. Since the center of gravity depends on the external field, its motion is harder to determine than the motion of the center of mass. The common method to deal with gravitational torques is a field theory.
.
characterize the center of gravity as a point about which there is no torque. In other words, the center of gravity is a point of application for the resultant force. Under this formulation, the center of gravity is defined as a point that satisfies the equation

where and are the total force and torque on the body due to gravity.
One complication concerning is that its defining equation is not generally solvable. If and are not orthogonal, then there is no solution; the force of gravity does not have a resultant and cannot be replaced by a single force at any point. There are some important special cases where and are guaranteed to be orthogonal, such as if all forces lie in a single plane or are aligned with a single point.
If the equation is solvable, there is another complication: its solutions are not unique. Instead, there are infinitely many solutions; the set of all solutions is known as the line of action
of the force. This line is parallel to the weight . In general, there is no way to choose a particular point as the unique center of gravity. A single point may still be chosen in some special cases, such as if the gravitational field is parallel or spherically symmetric. These cases are considered below.
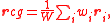
where is the (scalar) weight of the th particle and is the (scalar) total weight of all the particles. This equation always has a unique solution, and in the parallel-field approximation, it is compatible with the torque requirement.
A common illustration concerns the Moon
in the field of the Earth
. Using the weighted-average definition, the Moon has a center of gravity that is lower (closer to the Earth) than its center of mass, because its lower portion is more strongly influenced by the Earth's gravity.
:
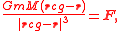
where is the gravitational constant
and is the mass of the body. As long as the total force is nonzero, this equation has a unique solution, and it satisfies the torque requirement. A convenient feature of this definition is that if the body is itself spherically symmetric, then lies at its center of mass. In general, as the distance between and the body increases, the center of gravity approaches the center of mass.
Another way to view this definition is to consider the gravitational field of the body; then is the apparent source of gravitational attraction for an observer located at . For this reason, is sometimes referred to as the center of gravity of relative to the point .
When it is necessary to consider a gravitational torque, it is easier to represent gravity as a force acting at the center of mass, plus an orientation-dependent couple
. The latter is best approached by treating the gravitational potential as a field
.
Physics
Physics is a natural science that involves the study of matter and its motion through spacetime, along with related concepts such as energy and force. More broadly, it is the general analysis of nature, conducted in order to understand how the universe behaves.Physics is one of the oldest academic...
, a center of gravity of a material body is a point that may be used for a summary description of gravitational interactions. In a uniform gravitational field, the center of mass
Center of mass
In physics, the center of mass or barycenter of a system is the average location of all of its mass. In the case of a rigid body, the position of the center of mass is fixed in relation to the body...
serves as the center of gravity. This is a very good approximation for smaller bodies near the surface of Earth, so there is no practical need to distinguish "center of gravity" from "center of mass" in most applications, such as engineering and medicine.
In a non-uniform field, gravitational effects such as potential energy
Potential energy
In physics, potential energy is the energy stored in a body or in a system due to its position in a force field or due to its configuration. The SI unit of measure for energy and work is the Joule...
, force
Force
In physics, a force is any influence that causes an object to undergo a change in speed, a change in direction, or a change in shape. In other words, a force is that which can cause an object with mass to change its velocity , i.e., to accelerate, or which can cause a flexible object to deform...
, and torque
Torque
Torque, moment or moment of force , is the tendency of a force to rotate an object about an axis, fulcrum, or pivot. Just as a force is a push or a pull, a torque can be thought of as a twist....
can no longer be calculated using the center of mass alone. In particular, a non-uniform gravitational field can produce a torque on an object, causing it to rotate. The center of gravity seeks to explain this effect. Formally, a center of gravity is an application point of the resultant gravitational force on the body. Such a point may not exist, and if it exists, it is not unique. One can further define a unique center of gravity by approximating the field as either parallel or spherically symmetric.
The concept of a center of gravity as distinct from the center of mass is rarely used in applications, even in celestial mechanics
Celestial mechanics
Celestial mechanics is the branch of astronomy that deals with the motions of celestial objects. The field applies principles of physics, historically classical mechanics, to astronomical objects such as stars and planets to produce ephemeris data. Orbital mechanics is a subfield which focuses on...
, where non-uniform fields are important. Since the center of gravity depends on the external field, its motion is harder to determine than the motion of the center of mass. The common method to deal with gravitational torques is a field theory.
Center of mass
One way to define the center of gravity of a body is as the unique point in the body, if it exists, that satisfies the following requirement: There is no torque about the point for any positioning of the body in the field of force in which it is placed. This center of gravity exists only when the force is uniform, in which case it coincides with the center of mass. This approach dates back to ArchimedesArchimedes
Archimedes of Syracuse was a Greek mathematician, physicist, engineer, inventor, and astronomer. Although few details of his life are known, he is regarded as one of the leading scientists in classical antiquity. Among his advances in physics are the foundations of hydrostatics, statics and an...
.
Centers of gravity in a field
When a body is affected by a non-uniform external gravitational field, one can sometimes define a center of gravity relative to that field that will act as a point where the gravitational force is applied. Textbooks such as the The Feynman Lectures on PhysicsThe Feynman Lectures on Physics
The Feynman Lectures on Physics is a 1964 physics textbook by Richard P. Feynman, Robert B. Leighton and Matthew Sands, based upon the lectures given by Feynman to undergraduate students at the California Institute of Technology in 1961–63. It includes lectures on mathematics, electromagnetism,...
characterize the center of gravity as a point about which there is no torque. In other words, the center of gravity is a point of application for the resultant force. Under this formulation, the center of gravity is defined as a point that satisfies the equation

where and are the total force and torque on the body due to gravity.
One complication concerning is that its defining equation is not generally solvable. If and are not orthogonal, then there is no solution; the force of gravity does not have a resultant and cannot be replaced by a single force at any point. There are some important special cases where and are guaranteed to be orthogonal, such as if all forces lie in a single plane or are aligned with a single point.
If the equation is solvable, there is another complication: its solutions are not unique. Instead, there are infinitely many solutions; the set of all solutions is known as the line of action
Line of action
In physics, the line of action of a force F expresses the geometry of how F is applied. It is the line through the point at which F is applied and along the direction in which F is applied....
of the force. This line is parallel to the weight . In general, there is no way to choose a particular point as the unique center of gravity. A single point may still be chosen in some special cases, such as if the gravitational field is parallel or spherically symmetric. These cases are considered below.
Parallel fields
Some of the inhomogeneity in a gravitational field may be modeled by a variable put parallel field: , where is some constant unit vector. Although a non-uniform gravitational field cannot be exactly parallel, this approximation can be valid if the body is sufficiently small. The center of gravity may then be defined as a certain weighted average of the locations of the particles composing the body. Whereas the center of mass averages over the mass of each particle, the center of gravity averages over the weight of each particle: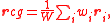
where is the (scalar) weight of the th particle and is the (scalar) total weight of all the particles. This equation always has a unique solution, and in the parallel-field approximation, it is compatible with the torque requirement.
A common illustration concerns the Moon
Moon
The Moon is Earth's only known natural satellite,There are a number of near-Earth asteroids including 3753 Cruithne that are co-orbital with Earth: their orbits bring them close to Earth for periods of time but then alter in the long term . These are quasi-satellites and not true moons. For more...
in the field of the Earth
Earth
Earth is the third planet from the Sun, and the densest and fifth-largest of the eight planets in the Solar System. It is also the largest of the Solar System's four terrestrial planets...
. Using the weighted-average definition, the Moon has a center of gravity that is lower (closer to the Earth) than its center of mass, because its lower portion is more strongly influenced by the Earth's gravity.
Spherically symmetric fields
If the external gravitational field is spherically symmetric, then it is equivalent to the field of a point mass at the center of symmetry . In this case, the center of gravity can be defined as the point at which the total force on the body is given by Newton's LawNewton's law of universal gravitation
Newton's law of universal gravitation states that every point mass in the universe attracts every other point mass with a force that is directly proportional to the product of their masses and inversely proportional to the square of the distance between them...
:
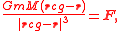
where is the gravitational constant
Gravitational constant
The gravitational constant, denoted G, is an empirical physical constant involved in the calculation of the gravitational attraction between objects with mass. It appears in Newton's law of universal gravitation and in Einstein's theory of general relativity. It is also known as the universal...
and is the mass of the body. As long as the total force is nonzero, this equation has a unique solution, and it satisfies the torque requirement. A convenient feature of this definition is that if the body is itself spherically symmetric, then lies at its center of mass. In general, as the distance between and the body increases, the center of gravity approaches the center of mass.
Another way to view this definition is to consider the gravitational field of the body; then is the apparent source of gravitational attraction for an observer located at . For this reason, is sometimes referred to as the center of gravity of relative to the point .
Usage
The centers of gravity defined above are not fixed points on the body; rather, they change as the position and orientation of the body changes. This characteristic makes the center of gravity difficult to work with, so the concept has little practical use.When it is necessary to consider a gravitational torque, it is easier to represent gravity as a force acting at the center of mass, plus an orientation-dependent couple
Couple (mechanics)
In mechanics, a couple is a system of forces with a resultant moment but no resultant force. Another term for a couple is a pure moment. Its effect is to create rotation without translation, or more generally without any acceleration of the centre of mass.The resultant moment of a couple is called...
. The latter is best approached by treating the gravitational potential as a field
Field (physics)
In physics, a field is a physical quantity associated with each point of spacetime. A field can be classified as a scalar field, a vector field, a spinor field, or a tensor field according to whether the value of the field at each point is a scalar, a vector, a spinor or, more generally, a tensor,...
.

