
Great-circle distance
Encyclopedia
The great-circle distance or orthodromic distance is the shortest distance
between any two point
s on the surface of a sphere
measured along a path on the surface of the sphere (as opposed to going through the sphere's interior). Because spherical geometry
is rather different from ordinary Euclidean geometry
, the equations for distance take on a different form. The distance between two points in Euclidean space
is the length of a straight line from one point to the other. On the sphere, however, there are no straight lines. In non-Euclidean geometry
, straight lines are replaced with geodesic
s. Geodesics on the sphere are the great circle
s (circles on the sphere whose centers are coincident with the center of the sphere).
Between any two different points on a sphere which are not directly opposite each other
, there is a unique great circle. The two points separate the great circle into two arcs. The length of the shorter arc is the great-circle distance between the points. A great circle endowed with such a distance is the Riemannian circle
.
Between two points which are directly opposite each other, called antipodal point
s, there are infinitely many great circles, but all great circle arcs between antipodal points have the same length, i.e. half the circumference
of the circle, or , where r is the radius
, where r is the radius
of the sphere
.
Because the Earth is nearly spherical (see Earth radius
) equations for great-circle distance can be used to roughly calculate the shortest distance between points on the surface of the Earth (as the crow flies
), and so have applications in navigation
.
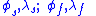 be the geographical latitude
be the geographical latitude
and longitude
of two points (a base "standpoint" and the destination "forepoint"), respectively, and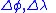 their differences; then
their differences; then  , the central angle
, the central angle
between them, is given by the spherical law of cosines:

The distance d, i.e. the arc length
, for a sphere of radius r and given in radian
given in radian
s, is then:

This arccosine formula above can have large rounding errors if the distance is small (if the two points are a kilometer apart the cosine of the central angle comes out 0.99999999). An equation known as the haversine formula
is numerically better-conditioned
for small distances:

Historically, the use of this formula was simplified by the availability of tables for the haversine function: hav(θ) = sin2 (θ/2).
Although this formula is accurate for most distances on a sphere, it too suffers from rounding errors for the special (and somewhat unusual) case of antipodal point
s (on opposite ends of the sphere). A more complicated formula that is accurate for all distances is the following special case (a sphere, which is an ellipsoid with equal major and minor axes) of the Vincenty formula
(which more generally is a method to compute distances on ellipsoids):

When programming a computer, one should use the unambiguously in all quadrants.
unambiguously in all quadrants.
If r is the great-circle radius of the sphere, then the great-circle distance is .
.
instead of latitude/longitude to describe the positions, is found by means of 3D vector algebra, i.e. utilizing the dot product
, cross product
, or a combination:

where and
and  are the n-vectors representing the two positions s and f. Similarly to the equations above based on latitude and longitude, the expression based on arctan is the only one that is well-conditioned for all angles. If the two positions are originally given as latitudes and longitudes, a conversion to n-vectors must first be performed.
are the n-vectors representing the two positions s and f. Similarly to the equations above based on latitude and longitude, the expression based on arctan is the only one that is well-conditioned for all angles. If the two positions are originally given as latitudes and longitudes, a conversion to n-vectors must first be performed.
between the two points can be determined from the chord length. The great circle distance is proportional to the central angle.
The great circle chord length may be calculated as follows for the corresponding unit sphere, by means of Cartesian subtraction
:

The central angle is:
The great circle distance is:

closely resembles a flattened sphere (a spheroid
) with equatorial radius of 6,378.137 km; distance
of 6,378.137 km; distance  from the center of the spheroid to each pole is 6356.752 km. When calculating the length of a short north-south line at the equator, the sphere that best approximates that part of the spheroid has a radius of
from the center of the spheroid to each pole is 6356.752 km. When calculating the length of a short north-south line at the equator, the sphere that best approximates that part of the spheroid has a radius of  , or 6,335.439 km, while the spheroid at the poles is best approximated by a sphere of radius
, or 6,335.439 km, while the spheroid at the poles is best approximated by a sphere of radius  , or 6,399.594 km, a 1% difference. So as long as we're assuming a spherical Earth, any single formula for distance on the Earth is only guaranteed correct within 0.5% (though we can do better if our formula is only intended to apply to a limited area). The average radius for a spherical approximation of the figure of the Earth
, or 6,399.594 km, a 1% difference. So as long as we're assuming a spherical Earth, any single formula for distance on the Earth is only guaranteed correct within 0.5% (though we can do better if our formula is only intended to apply to a limited area). The average radius for a spherical approximation of the figure of the Earth
with respect to surface is approximately 6371.01 km, while the quadratic mean or root mean square
approximation of the average great-circle circumference
derives a radius of about 6372.8 km.
and longitude
of two airports:
First convert the co-ordinates to decimal degrees
Plug these values into the spherical law of cosines:

 comes out to be 25.958 degrees, or 0.45306 radians, and the great-circle distance is the assumed radius times that angle:
comes out to be 25.958 degrees, or 0.45306 radians, and the great-circle distance is the assumed radius times that angle:

So assuming a spherical earth, distance between LAX and BNA is about 2887 km or 1794 statute miles (× 0.621371) or 1559 nautical miles (× 0.539957). Geodesic distance between the given coordinates on the GRS 80
/WGS 84 spheroid is 2892.777 km.
Distance
Distance is a numerical description of how far apart objects are. In physics or everyday discussion, distance may refer to a physical length, or an estimation based on other criteria . In mathematics, a distance function or metric is a generalization of the concept of physical distance...
between any two point
Point (geometry)
In geometry, topology and related branches of mathematics a spatial point is a primitive notion upon which other concepts may be defined. In geometry, points are zero-dimensional; i.e., they do not have volume, area, length, or any other higher-dimensional analogue. In branches of mathematics...
s on the surface of a sphere
Sphere
A sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...
measured along a path on the surface of the sphere (as opposed to going through the sphere's interior). Because spherical geometry
Spherical geometry
Spherical geometry is the geometry of the two-dimensional surface of a sphere. It is an example of a geometry which is not Euclidean. Two practical applications of the principles of spherical geometry are to navigation and astronomy....
is rather different from ordinary Euclidean geometry
Euclidean geometry
Euclidean geometry is a mathematical system attributed to the Alexandrian Greek mathematician Euclid, which he described in his textbook on geometry: the Elements. Euclid's method consists in assuming a small set of intuitively appealing axioms, and deducing many other propositions from these...
, the equations for distance take on a different form. The distance between two points in Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
is the length of a straight line from one point to the other. On the sphere, however, there are no straight lines. In non-Euclidean geometry
Non-Euclidean geometry
Non-Euclidean geometry is the term used to refer to two specific geometries which are, loosely speaking, obtained by negating the Euclidean parallel postulate, namely hyperbolic and elliptic geometry. This is one term which, for historical reasons, has a meaning in mathematics which is much...
, straight lines are replaced with geodesic
Geodesic
In mathematics, a geodesic is a generalization of the notion of a "straight line" to "curved spaces". In the presence of a Riemannian metric, geodesics are defined to be the shortest path between points in the space...
s. Geodesics on the sphere are the great circle
Great circle
A great circle, also known as a Riemannian circle, of a sphere is the intersection of the sphere and a plane which passes through the center point of the sphere, as opposed to a general circle of a sphere where the plane is not required to pass through the center...
s (circles on the sphere whose centers are coincident with the center of the sphere).
Between any two different points on a sphere which are not directly opposite each other
Antipodal point
In mathematics, the antipodal point of a point on the surface of a sphere is the point which is diametrically opposite to it — so situated that a line drawn from the one to the other passes through the centre of the sphere and forms a true diameter....
, there is a unique great circle. The two points separate the great circle into two arcs. The length of the shorter arc is the great-circle distance between the points. A great circle endowed with such a distance is the Riemannian circle
Riemannian circle
In metric space theory and Riemannian geometry, the Riemannian circle is a great circle equipped with its great-circle distance...
.
Between two points which are directly opposite each other, called antipodal point
Antipodal point
In mathematics, the antipodal point of a point on the surface of a sphere is the point which is diametrically opposite to it — so situated that a line drawn from the one to the other passes through the centre of the sphere and forms a true diameter....
s, there are infinitely many great circles, but all great circle arcs between antipodal points have the same length, i.e. half the circumference
Circumference
The circumference is the distance around a closed curve. Circumference is a special perimeter.-Circumference of a circle:The circumference of a circle is the length around it....
of the circle, or
 , where r is the radius
, where r is the radiusRadius
In classical geometry, a radius of a circle or sphere is any line segment from its center to its perimeter. By extension, the radius of a circle or sphere is the length of any such segment, which is half the diameter. If the object does not have an obvious center, the term may refer to its...
of the sphere
Sphere
A sphere is a perfectly round geometrical object in three-dimensional space, such as the shape of a round ball. Like a circle in two dimensions, a perfect sphere is completely symmetrical around its center, with all points on the surface lying the same distance r from the center point...
.
Because the Earth is nearly spherical (see Earth radius
Earth radius
Because the Earth is not perfectly spherical, no single value serves as its natural radius. Distances from points on the surface to the center range from 6,353 km to 6,384 km...
) equations for great-circle distance can be used to roughly calculate the shortest distance between points on the surface of the Earth (as the crow flies
As the crow flies
"As the crow flies" or beelining is an idiom for the shortest route between two points; the geodesic distance.An example is the great-circle distance between Key West and Pensacola, at either end of the U.S...
), and so have applications in navigation
Navigation
Navigation is the process of monitoring and controlling the movement of a craft or vehicle from one place to another. It is also the term of art used for the specialized knowledge used by navigators to perform navigation tasks...
.
Formulas
Let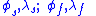 be the geographical latitude
be the geographical latitudeLatitude
In geography, the latitude of a location on the Earth is the angular distance of that location south or north of the Equator. The latitude is an angle, and is usually measured in degrees . The equator has a latitude of 0°, the North pole has a latitude of 90° north , and the South pole has a...
and longitude
Longitude
Longitude is a geographic coordinate that specifies the east-west position of a point on the Earth's surface. It is an angular measurement, usually expressed in degrees, minutes and seconds, and denoted by the Greek letter lambda ....
of two points (a base "standpoint" and the destination "forepoint"), respectively, and
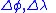 their differences; then
their differences; then  , the central angle
, the central angleCentral angle
A central angle is an angle which vertex is the center of a circle, and whose sides pass through a pair of points on the circle, thereby subtending an arc between those two points whose angle is equal to the central angle itself...
between them, is given by the spherical law of cosines:

The distance d, i.e. the arc length
Arc length
Determining the length of an irregular arc segment is also called rectification of a curve. Historically, many methods were used for specific curves...
, for a sphere of radius r and
 given in radian
given in radianRadian
Radian is the ratio between the length of an arc and its radius. The radian is the standard unit of angular measure, used in many areas of mathematics. The unit was formerly a SI supplementary unit, but this category was abolished in 1995 and the radian is now considered a SI derived unit...
s, is then:

This arccosine formula above can have large rounding errors if the distance is small (if the two points are a kilometer apart the cosine of the central angle comes out 0.99999999). An equation known as the haversine formula
Haversine formula
The haversine formula is an equation important in navigation, giving great-circle distances between two points on a sphere from their longitudes and latitudes...
is numerically better-conditioned
Condition number
In the field of numerical analysis, the condition number of a function with respect to an argument measures the asymptotically worst case of how much the function can change in proportion to small changes in the argument...
for small distances:

Historically, the use of this formula was simplified by the availability of tables for the haversine function: hav(θ) = sin2 (θ/2).
Although this formula is accurate for most distances on a sphere, it too suffers from rounding errors for the special (and somewhat unusual) case of antipodal point
Antipodal point
In mathematics, the antipodal point of a point on the surface of a sphere is the point which is diametrically opposite to it — so situated that a line drawn from the one to the other passes through the centre of the sphere and forms a true diameter....
s (on opposite ends of the sphere). A more complicated formula that is accurate for all distances is the following special case (a sphere, which is an ellipsoid with equal major and minor axes) of the Vincenty formula
Vincenty's formulae
Vincenty's formulae are two related iterative methods used in geodesy to calculate the distance between two points on the surface of a spheroid, developed by Thaddeus Vincenty They are based on the assumption that the figure of the Earth is an oblate spheroid, and hence are more accurate than...
(which more generally is a method to compute distances on ellipsoids):

When programming a computer, one should use the
atan2Atan2In trigonometry, the two-argument function atan2 is a variation of the arctangent function. For any real arguments and not both equal to zero, is the angle in radians between the positive -axis of a plane and the point given by the coordinates on it...
function rather than the ordinary arctangent function (atan), in order to simplify handling of the case where the denominator is zero, and to compute  unambiguously in all quadrants.
unambiguously in all quadrants.If r is the great-circle radius of the sphere, then the great-circle distance is
 .
.Vector version
Another representation of similar formulas, but using n-vectorN-vector
n-vector is a three parameter non-singular horizontal position representation well-suited for replacing latitude and longitude in mathematical calculations and computer algorithms. Geometrically, it is a unit vector that is normal to the reference ellipsoid. The vector is decomposed in an Earth...
instead of latitude/longitude to describe the positions, is found by means of 3D vector algebra, i.e. utilizing the dot product
Dot product
In mathematics, the dot product or scalar product is an algebraic operation that takes two equal-length sequences of numbers and returns a single number obtained by multiplying corresponding entries and then summing those products...
, cross product
Cross product
In mathematics, the cross product, vector product, or Gibbs vector product is a binary operation on two vectors in three-dimensional space. It results in a vector which is perpendicular to both of the vectors being multiplied and normal to the plane containing them...
, or a combination:

where
 and
and  are the n-vectors representing the two positions s and f. Similarly to the equations above based on latitude and longitude, the expression based on arctan is the only one that is well-conditioned for all angles. If the two positions are originally given as latitudes and longitudes, a conversion to n-vectors must first be performed.
are the n-vectors representing the two positions s and f. Similarly to the equations above based on latitude and longitude, the expression based on arctan is the only one that is well-conditioned for all angles. If the two positions are originally given as latitudes and longitudes, a conversion to n-vectors must first be performed.From chord length
A line through three-dimensional space between points of interest on a spherical Earth is the chord of the great circle between the points. The central angleCentral angle
A central angle is an angle which vertex is the center of a circle, and whose sides pass through a pair of points on the circle, thereby subtending an arc between those two points whose angle is equal to the central angle itself...
between the two points can be determined from the chord length. The great circle distance is proportional to the central angle.
The great circle chord length may be calculated as follows for the corresponding unit sphere, by means of Cartesian subtraction
Cartesian coordinate system
A Cartesian coordinate system specifies each point uniquely in a plane by a pair of numerical coordinates, which are the signed distances from the point to two fixed perpendicular directed lines, measured in the same unit of length...
:

The central angle is:

The great circle distance is:

Spherical cosine for sides derivation
By using Cartesian products rather than differences, the origin of the spherical cosine for sides becomes apparent:
Radius for spherical Earth
The shape of the EarthGeoid
The geoid is that equipotential surface which would coincide exactly with the mean ocean surface of the Earth, if the oceans were in equilibrium, at rest , and extended through the continents . According to C.F...
closely resembles a flattened sphere (a spheroid
Spheroid
A spheroid, or ellipsoid of revolution is a quadric surface obtained by rotating an ellipse about one of its principal axes; in other words, an ellipsoid with two equal semi-diameters....
) with equatorial radius
 of 6,378.137 km; distance
of 6,378.137 km; distance  from the center of the spheroid to each pole is 6356.752 km. When calculating the length of a short north-south line at the equator, the sphere that best approximates that part of the spheroid has a radius of
from the center of the spheroid to each pole is 6356.752 km. When calculating the length of a short north-south line at the equator, the sphere that best approximates that part of the spheroid has a radius of  , or 6,335.439 km, while the spheroid at the poles is best approximated by a sphere of radius
, or 6,335.439 km, while the spheroid at the poles is best approximated by a sphere of radius  , or 6,399.594 km, a 1% difference. So as long as we're assuming a spherical Earth, any single formula for distance on the Earth is only guaranteed correct within 0.5% (though we can do better if our formula is only intended to apply to a limited area). The average radius for a spherical approximation of the figure of the Earth
, or 6,399.594 km, a 1% difference. So as long as we're assuming a spherical Earth, any single formula for distance on the Earth is only guaranteed correct within 0.5% (though we can do better if our formula is only intended to apply to a limited area). The average radius for a spherical approximation of the figure of the EarthFigure of the Earth
The expression figure of the Earth has various meanings in geodesy according to the way it is used and the precision with which the Earth's size and shape is to be defined. The actual topographic surface is most apparent with its variety of land forms and water areas. This is, in fact, the surface...
with respect to surface is approximately 6371.01 km, while the quadratic mean or root mean square
Root mean square
In mathematics, the root mean square , also known as the quadratic mean, is a statistical measure of the magnitude of a varying quantity. It is especially useful when variates are positive and negative, e.g., sinusoids...
approximation of the average great-circle circumference
Great circle
A great circle, also known as a Riemannian circle, of a sphere is the intersection of the sphere and a plane which passes through the center point of the sphere, as opposed to a general circle of a sphere where the plane is not required to pass through the center...
derives a radius of about 6372.8 km.
Worked example
For an example of the formula in practice, take the latitudeLatitude
In geography, the latitude of a location on the Earth is the angular distance of that location south or north of the Equator. The latitude is an angle, and is usually measured in degrees . The equator has a latitude of 0°, the North pole has a latitude of 90° north , and the South pole has a...
and longitude
Longitude
Longitude is a geographic coordinate that specifies the east-west position of a point on the Earth's surface. It is an angular measurement, usually expressed in degrees, minutes and seconds, and denoted by the Greek letter lambda ....
of two airports:
- Nashville International Airport (BNA) in Nashville, TN, USA: N 36°7.2', W 86°40.2'
- Los Angeles International Airport (LAX) in Los Angeles, CA, USA: N 33°56.4', W 118°24.0'
First convert the co-ordinates to decimal degrees
Geographic coordinate conversion
-Ways of writing coordinates:All of the following are valid and acceptable ways to write geographic coordinates:* 40:26:46N,79:56:55W* 40:26:46.302N 79:56:55.903W* 40°26′47″N 79°58′36″W* 40d 26′ 47″ N 79d 58′ 36″ W* 40.446195N 79.948862W...
- BNA:

- LAX:

Plug these values into the spherical law of cosines:

 comes out to be 25.958 degrees, or 0.45306 radians, and the great-circle distance is the assumed radius times that angle:
comes out to be 25.958 degrees, or 0.45306 radians, and the great-circle distance is the assumed radius times that angle:
So assuming a spherical earth, distance between LAX and BNA is about 2887 km or 1794 statute miles (× 0.621371) or 1559 nautical miles (× 0.539957). Geodesic distance between the given coordinates on the GRS 80
GRS 80
GRS 80, or Geodetic Reference System 1980, is a geodetic reference system consisting of a global reference ellipsoid and a gravity field model.-Geodesy:...
/WGS 84 spheroid is 2892.777 km.
See also
- Air navigationAir navigationThe basic principles of air navigation are identical to general navigation, which includes the process of planning, recording, and controlling the movement of a craft from one place to another....
- Central angleCentral angleA central angle is an angle which vertex is the center of a circle, and whose sides pass through a pair of points on the circle, thereby subtending an arc between those two points whose angle is equal to the central angle itself...
- CircumnavigationCircumnavigationCircumnavigation – literally, "navigation of a circumference" – refers to travelling all the way around an island, a continent, or the entire planet Earth.- Global circumnavigation :...
- Flight planningFlight planningFlight planning is the process of producing a flight plan to describe a proposed aircraft flight. It involves two safety-critical aspects: fuel calculation, to ensure that the aircraft can safely reach the destination, and compliance with air traffic control requirements, to minimise the risk of...
- GeodesyGeodesyGeodesy , also named geodetics, a branch of earth sciences, is the scientific discipline that deals with the measurement and representation of the Earth, including its gravitational field, in a three-dimensional time-varying space. Geodesists also study geodynamical phenomena such as crustal...
- Geodetic systemGeodetic systemGeodetic systems or geodetic data are used in geodesy, navigation, surveying by cartographers and satellite navigation systems to translate positions indicated on their products to their real position on earth....
- Geographical distanceGeographical distanceGeographical distance is the distance measured along the surface of the earth. The formulae in this article calculate distances between points which are defined by geographical coordinates in terms of latitude and longitude.-An abstraction:...
- Great-circle navigationGreat-circle navigationGreat-circle navigation is the practice of navigating a vessel along a track that follows a great circle. A great circle track is the shortest distance between two points on the surface of a planetary body, assuming a perfect spherical model.-Methods:In order to construct a great circle track,...
- Haversine formulaHaversine formulaThe haversine formula is an equation important in navigation, giving great-circle distances between two points on a sphere from their longitudes and latitudes...
- Meridian arcMeridian arcIn geodesy, a meridian arc measurement is a highly accurate determination of the distance between two points with the same longitude. Two or more such determinations at different locations then specify the shape of the reference ellipsoid which best approximates the shape of the geoid. This...
- Spherical EarthSpherical EarthThe concept of a spherical Earth dates back to ancient Greek philosophy from around the 6th century BC, but remained a matter of philosophical speculation until the 3rd century BC when Hellenistic astronomy established the spherical shape of the earth as a physical given...
- Spherical geometrySpherical geometrySpherical geometry is the geometry of the two-dimensional surface of a sphere. It is an example of a geometry which is not Euclidean. Two practical applications of the principles of spherical geometry are to navigation and astronomy....
- Spherical trigonometrySpherical trigonometrySpherical trigonometry is a branch of spherical geometry which deals with polygons on the sphere and the relationships between the sides and the angles...
- Vincenty's formulaeVincenty's formulaeVincenty's formulae are two related iterative methods used in geodesy to calculate the distance between two points on the surface of a spheroid, developed by Thaddeus Vincenty They are based on the assumption that the figure of the Earth is an oblate spheroid, and hence are more accurate than...
External links
- GreatCircle at MathWorldMathWorldMathWorld is an online mathematics reference work, created and largely written by Eric W. Weisstein. It is sponsored by and licensed to Wolfram Research, Inc. and was partially funded by the National Science Foundation's National Science Digital Library grant to the University of Illinois at...
- Global Distance Calculator at Infoplease (Warning: website uses pop-under ads).
- Haversine formula in JavaScript Haversine and other formulae for calculating distances, bearings, etc.
- Distance Between Two Cities Site uses Haversine Formulae and integrates Road distances too
- Distance Between Two Cities Places On Map.
- Distance Between Cities Calculator
- 3D First and Second Problem 3D javascript interactive tool (Google ChromeGoogle ChromeGoogle Chrome is a web browser developed by Google that uses the WebKit layout engine. It was first released as a beta version for Microsoft Windows on September 2, 2008, and the public stable release was on December 11, 2008. The name is derived from the graphical user interface frame, or...
, Firefox).

