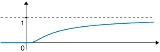
Non-analytic smooth function
Encyclopedia
In mathematics
, smooth function
s (also called infinitely differentiable functions) and analytic function
s are two very important types of functions
. One can easily prove that any analytic function of a real
argument is smooth. The converse
is not true, with this article constructing a counterexample
.
One of the most important applications of smooth functions with compact support is the construction of so-called mollifier
s, which are important in theories of generalized function
s, like e.g. Laurent Schwartz
's theory of distribution
s.
The existence of smooth but non-analytic functions represents one of the main differences between differential geometry and analytic geometry
. In terms of sheaf theory, this difference can be stated as follows: the sheaf of differentiable functions on a differentiable manifold
is fine, in contrast with the analytic case.
The functions below are generally used to build up partitions of unity on differentiable manifolds.
 Consider the function
Consider the function

defined for every real number
x.
, given by

where pn(x) is a polynomial of degree n − 1 given recursively by p1(x) = 1 and

m including zero,

which implies that all f (n) are continuous and differentiable at x = 0, because


because all the positive terms for n ≠ m + 1 are added. Therefore, using the functional equation
of the exponential function
,

We now prove the formula for the nth derivative of f by mathematical induction
. Using the chain rule
, the reciprocal rule
, and the fact that the derivative of the exponential function is again the exponential function, we see that the formula is correct for the first derivative of f for all x > 0 and that p1(x) is a polynomial of degree 0. Of course, the derivative of f is zero for x < 0.
It remains to show that the right-hand side derivative of f at x = 0 is zero. Using the above limit, we see that

The induction step from n to n + 1 is similar. For x > 0 we get for the derivative
where pn+1(x) is a polynomial of degree n = (n + 1) − 1. Of course, the (n + 1)st derivative of f is zero for x < 0. For the right-hand side derivative of f (n) at x = 0 we obtain with the above limit

are 0. Therefore, the Taylor series
of f at the origin converges everywhere to the zero function,

and so the Taylor series does not equal f(x) for x > 0. Consequently, f is not analytic
at the origin. This pathology cannot occur with differentiable functions of a complex variable
rather than of a real variable. Indeed, all holomorphic functions are analytic
, so that the failure of f to be analytic in spite of its being infinitely differentiable is an indication of one of the most dramatic differences between real-variable and complex-variable analysis.
Note that although the function f has derivatives of all orders over the real line, the analytic continuation
of f from the positive half-line x > 0 to the complex plane
, that is, the function

has an essential singularity
at the origin, and hence is not even continuous, much less analytic. By the great Picard theorem, it attains every complex value (with the exception of zero) infinitely often in every neighbourhood of the origin.
as follows. Let A:={2n : n ∈ N } be the set of all powers of 2, and define for all x ∈ R
Since the series converge for all n ∈ N, this function is easily seen to be of class C∞, by a standard inductive application of the Weierstrass M-test, and of the theorem of limit under the sign of derivative.
converge for all n ∈ N, this function is easily seen to be of class C∞, by a standard inductive application of the Weierstrass M-test, and of the theorem of limit under the sign of derivative.
Moreover, for any dyadic rational
multiple of π, that is x:=π p/q with p ∈ N and q ∈ A, and for all order of derivation n ∈ A , n ≥ 4 and n > q we have

where we used the fact that cos(kx)=1 for all k > q. As a consequence, at any such x ∈ R

so that the radius of convergence
of the Taylor series
of f at x is 0 by the Cauchy-Hadamard formula . Since the set of analyticity of a function is an open set, and since dyadic rationals are dense, we conclude that f is nowhere analytic in R.

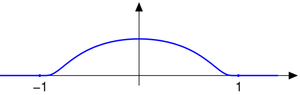
has a strictly positive denominator everywhere on the real line, hence g is also smooth. Furthermore, g(x) = 0 for x ≤ 0 and g(x) = 1 for x ≥ 1, hence it provides a smooth transition from the level 0 to the level 1 in the unit interval
[ 0,1] . To have the smooth transition in the real interval [ a,b] with a < b, consider the function

For real numbers , the smooth function

equals 1 on the closed interval[ b,c] and vanishes outside the open interval (a,d).
of a smooth function. This result is known as Borel's lemma
, after Émile Borel
.
With the smooth transition function g as above, define

This function h is also smooth; it equals 1 on the closed interval[ −1,1] and vanishes outside the open interval (−2,2). Using h, define for every natural number n (including zero) the smooth function

which agrees with the monomial
xn on[ −1,1] and vanishes outside the interval (−2,2). Hence, the k-th derivative of ψn at the origin satisfies

and the boundedness theorem implies that ψn and every derivative of ψn is bounded. Therefore, the constants

involving the supremum norm of ψn and its first n derivatives, are well-defined real numbers. Define the scaled functions

By repeated application of the chain rule
,

and, using the previous result for the k-th derivative of ψn at zero,

It remains to show that the function

is well defined and can be differentiated term-by-term infinitely often. To this end, observe that for every k

where the remaining infinite series converges by the ratio test.
 For every radius r > 0,
For every radius r > 0,

with Euclidean norm ||x|| defines a smooth function on n-dimensional Euclidean space
with support
in the ball
of radius r.
Mathematics
Mathematics is the study of quantity, space, structure, and change. Mathematicians seek out patterns and formulate new conjectures. Mathematicians resolve the truth or falsity of conjectures by mathematical proofs, which are arguments sufficient to convince other mathematicians of their validity...
, smooth function
Smooth function
In mathematical analysis, a differentiability class is a classification of functions according to the properties of their derivatives. Higher order differentiability classes correspond to the existence of more derivatives. Functions that have derivatives of all orders are called smooth.Most of...
s (also called infinitely differentiable functions) and analytic function
Analytic function
In mathematics, an analytic function is a function that is locally given by a convergent power series. There exist both real analytic functions and complex analytic functions, categories that are similar in some ways, but different in others...
s are two very important types of functions
Function (mathematics)
In mathematics, a function associates one quantity, the argument of the function, also known as the input, with another quantity, the value of the function, also known as the output. A function assigns exactly one output to each input. The argument and the value may be real numbers, but they can...
. One can easily prove that any analytic function of a real
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
argument is smooth. The converse
Converse (logic)
In logic, the converse of a categorical or implicational statement is the result of reversing its two parts. For the implication P → Q, the converse is Q → P. For the categorical proposition All S is P, the converse is All P is S. In neither case does the converse necessarily follow from...
is not true, with this article constructing a counterexample
Counterexample
In logic, and especially in its applications to mathematics and philosophy, a counterexample is an exception to a proposed general rule. For example, consider the proposition "all students are lazy"....
.
One of the most important applications of smooth functions with compact support is the construction of so-called mollifier
Mollifier
In mathematics, mollifiers are smooth functions with special properties, used in distribution theory to create sequences of smooth functions approximating nonsmooth functions, via convolution...
s, which are important in theories of generalized function
Generalized function
In mathematics, generalized functions are objects generalizing the notion of functions. There is more than one recognized theory. Generalized functions are especially useful in making discontinuous functions more like smooth functions, and describing physical phenomena such as point charges...
s, like e.g. Laurent Schwartz
Laurent Schwartz
Laurent-Moïse Schwartz was a French mathematician. He pioneered the theory of distributions, which gives a well-defined meaning to objects such as the Dirac delta function. He was awarded the Fields medal in 1950 for his work...
's theory of distribution
Distribution (mathematics)
In mathematical analysis, distributions are objects that generalize functions. Distributions make it possible to differentiate functions whose derivatives do not exist in the classical sense. In particular, any locally integrable function has a distributional derivative...
s.
The existence of smooth but non-analytic functions represents one of the main differences between differential geometry and analytic geometry
Complex manifold
In differential geometry, a complex manifold is a manifold with an atlas of charts to the open unit disk in Cn, such that the transition maps are holomorphic....
. In terms of sheaf theory, this difference can be stated as follows: the sheaf of differentiable functions on a differentiable manifold
Differentiable manifold
A differentiable manifold is a type of manifold that is locally similar enough to a linear space to allow one to do calculus. Any manifold can be described by a collection of charts, also known as an atlas. One may then apply ideas from calculus while working within the individual charts, since...
is fine, in contrast with the analytic case.
The functions below are generally used to build up partitions of unity on differentiable manifolds.
Definition of the function


defined for every real number
Real number
In mathematics, a real number is a value that represents a quantity along a continuum, such as -5 , 4/3 , 8.6 , √2 and π...
x.
The function is smooth
The function f has continuous derivatives of all orders in all points x of the real lineReal line
In mathematics, the real line, or real number line is the line whose points are the real numbers. That is, the real line is the set of all real numbers, viewed as a geometric space, namely the Euclidean space of dimension one...
, given by

where pn(x) is a polynomial of degree n − 1 given recursively by p1(x) = 1 and

Outline of proof
The proof, by induction, is based on the fact that for any natural numberNatural number
In mathematics, the natural numbers are the ordinary whole numbers used for counting and ordering . These purposes are related to the linguistic notions of cardinal and ordinal numbers, respectively...
m including zero,

which implies that all f (n) are continuous and differentiable at x = 0, because

Detailed proof
By the power series representation of the exponential function, we have for every natural number m (including zero)
because all the positive terms for n ≠ m + 1 are added. Therefore, using the functional equation
Functional equation
In mathematics, a functional equation is any equation that specifies a function in implicit form.Often, the equation relates the value of a function at some point with its values at other points. For instance, properties of functions can be determined by considering the types of functional...
of the exponential function
Exponential function
In mathematics, the exponential function is the function ex, where e is the number such that the function ex is its own derivative. The exponential function is used to model a relationship in which a constant change in the independent variable gives the same proportional change In mathematics,...
,

We now prove the formula for the nth derivative of f by mathematical induction
Mathematical induction
Mathematical induction is a method of mathematical proof typically used to establish that a given statement is true of all natural numbers...
. Using the chain rule
Chain rule
In calculus, the chain rule is a formula for computing the derivative of the composition of two or more functions. That is, if f is a function and g is a function, then the chain rule expresses the derivative of the composite function in terms of the derivatives of f and g.In integration, the...
, the reciprocal rule
Reciprocal rule
In calculus, the reciprocal rule is a shorthand method of finding the derivative of a function that is the reciprocal of a differentiable function, without using the quotient rule or chain rule....
, and the fact that the derivative of the exponential function is again the exponential function, we see that the formula is correct for the first derivative of f for all x > 0 and that p1(x) is a polynomial of degree 0. Of course, the derivative of f is zero for x < 0.
It remains to show that the right-hand side derivative of f at x = 0 is zero. Using the above limit, we see that

The induction step from n to n + 1 is similar. For x > 0 we get for the derivative

where pn+1(x) is a polynomial of degree n = (n + 1) − 1. Of course, the (n + 1)st derivative of f is zero for x < 0. For the right-hand side derivative of f (n) at x = 0 we obtain with the above limit

The function is not analytic
As seen earlier, the function f is smooth, and all its derivatives at the originOrigin (mathematics)
In mathematics, the origin of a Euclidean space is a special point, usually denoted by the letter O, used as a fixed point of reference for the geometry of the surrounding space. In a Cartesian coordinate system, the origin is the point where the axes of the system intersect...
are 0. Therefore, the Taylor series
Taylor series
In mathematics, a Taylor series is a representation of a function as an infinite sum of terms that are calculated from the values of the function's derivatives at a single point....
of f at the origin converges everywhere to the zero function,

and so the Taylor series does not equal f(x) for x > 0. Consequently, f is not analytic
Analytic function
In mathematics, an analytic function is a function that is locally given by a convergent power series. There exist both real analytic functions and complex analytic functions, categories that are similar in some ways, but different in others...
at the origin. This pathology cannot occur with differentiable functions of a complex variable
Complex analysis
Complex analysis, traditionally known as the theory of functions of a complex variable, is the branch of mathematical analysis that investigates functions of complex numbers. It is useful in many branches of mathematics, including number theory and applied mathematics; as well as in physics,...
rather than of a real variable. Indeed, all holomorphic functions are analytic
Holomorphic functions are analytic
In complex analysis, a branch of mathematics, a complex-valued function ƒ of a complex variable z.*is said to be holomorphic at a point a if it is differentiable at every point within some open disk centered at a, and...
, so that the failure of f to be analytic in spite of its being infinitely differentiable is an indication of one of the most dramatic differences between real-variable and complex-variable analysis.
Note that although the function f has derivatives of all orders over the real line, the analytic continuation
Analytic continuation
In complex analysis, a branch of mathematics, analytic continuation is a technique to extend the domain of a given analytic function. Analytic continuation often succeeds in defining further values of a function, for example in a new region where an infinite series representation in terms of which...
of f from the positive half-line x > 0 to the complex plane
Complex plane
In mathematics, the complex plane or z-plane is a geometric representation of the complex numbers established by the real axis and the orthogonal imaginary axis...
, that is, the function

has an essential singularity
Essential singularity
In complex analysis, an essential singularity of a function is a "severe" singularity near which the function exhibits extreme behavior.The category essential singularity is a "left-over" or default group of singularities that are especially unmanageable: by definition they fit into neither of the...
at the origin, and hence is not even continuous, much less analytic. By the great Picard theorem, it attains every complex value (with the exception of zero) infinitely often in every neighbourhood of the origin.
A smooth function which is nowhere real analytic
A more pathological example, of an infinitely differentiable function which is not analytic at any point can be constructed by means of a Fourier seriesFourier series
In mathematics, a Fourier series decomposes periodic functions or periodic signals into the sum of a set of simple oscillating functions, namely sines and cosines...
as follows. Let A:={2n : n ∈ N } be the set of all powers of 2, and define for all x ∈ R

Since the series
 converge for all n ∈ N, this function is easily seen to be of class C∞, by a standard inductive application of the Weierstrass M-test, and of the theorem of limit under the sign of derivative.
converge for all n ∈ N, this function is easily seen to be of class C∞, by a standard inductive application of the Weierstrass M-test, and of the theorem of limit under the sign of derivative.Moreover, for any dyadic rational
Dyadic rational
In mathematics, a dyadic fraction or dyadic rational is a rational number whose denominator is a power of two, i.e., a number of the form a/2b where a is an integer and b is a natural number; for example, 1/2 or 3/8, but not 1/3...
multiple of π, that is x:=π p/q with p ∈ N and q ∈ A, and for all order of derivation n ∈ A , n ≥ 4 and n > q we have

where we used the fact that cos(kx)=1 for all k > q. As a consequence, at any such x ∈ R

so that the radius of convergence
Radius of convergence
In mathematics, the radius of convergence of a power series is a quantity, either a non-negative real number or ∞, that represents a domain in which the series will converge. Within the radius of convergence, a power series converges absolutely and uniformly on compacta as well...
of the Taylor series
Taylor series
In mathematics, a Taylor series is a representation of a function as an infinite sum of terms that are calculated from the values of the function's derivatives at a single point....
of f at x is 0 by the Cauchy-Hadamard formula . Since the set of analyticity of a function is an open set, and since dyadic rationals are dense, we conclude that f is nowhere analytic in R.
Smooth transition functions
The function
has a strictly positive denominator everywhere on the real line, hence g is also smooth. Furthermore, g(x) = 0 for x ≤ 0 and g(x) = 1 for x ≥ 1, hence it provides a smooth transition from the level 0 to the level 1 in the unit interval
Unit interval
In mathematics, the unit interval is the closed interval , that is, the set of all real numbers that are greater than or equal to 0 and less than or equal to 1...

For real numbers , the smooth function

equals 1 on the closed interval
Application to Taylor series
For every sequence α0, α1, α2, . . . of real or complex numbers, the following construction shows the existence of a smooth function F on the real line which has these numbers as derivatives at the origin. In particular, every sequence of numbers can appear as the coefficients of the Taylor seriesTaylor series
In mathematics, a Taylor series is a representation of a function as an infinite sum of terms that are calculated from the values of the function's derivatives at a single point....
of a smooth function. This result is known as Borel's lemma
Borel's lemma
In mathematics, Borel's lemma is an important result about partial differential equations named after Émile Borel.Suppose U is an open set in the Euclidean space Rn, and suppose that f_0, f_1, ... is a sequence of smooth, complex-valued functions on U...
, after Émile Borel
Émile Borel
Félix Édouard Justin Émile Borel was a French mathematician and politician.Borel was born in Saint-Affrique, Aveyron. Along with René-Louis Baire and Henri Lebesgue, he was among the pioneers of measure theory and its application to probability theory. The concept of a Borel set is named in his...
.
With the smooth transition function g as above, define

This function h is also smooth; it equals 1 on the closed interval

which agrees with the monomial
Monomial
In mathematics, in the context of polynomials, the word monomial can have one of two different meanings:*The first is a product of powers of variables, or formally any value obtained by finitely many multiplications of a variable. If only a single variable x is considered, this means that any...
xn on

and the boundedness theorem implies that ψn and every derivative of ψn is bounded. Therefore, the constants

involving the supremum norm of ψn and its first n derivatives, are well-defined real numbers. Define the scaled functions

By repeated application of the chain rule
Chain rule
In calculus, the chain rule is a formula for computing the derivative of the composition of two or more functions. That is, if f is a function and g is a function, then the chain rule expresses the derivative of the composite function in terms of the derivatives of f and g.In integration, the...
,

and, using the previous result for the k-th derivative of ψn at zero,

It remains to show that the function

is well defined and can be differentiated term-by-term infinitely often. To this end, observe that for every k

where the remaining infinite series converges by the ratio test.
Application to higher dimensions


with Euclidean norm ||x|| defines a smooth function on n-dimensional Euclidean space
Euclidean space
In mathematics, Euclidean space is the Euclidean plane and three-dimensional space of Euclidean geometry, as well as the generalizations of these notions to higher dimensions...
with support
Support (mathematics)
In mathematics, the support of a function is the set of points where the function is not zero, or the closure of that set . This concept is used very widely in mathematical analysis...
in the ball
Ball (mathematics)
In mathematics, a ball is the space inside a sphere. It may be a closed ball or an open ball ....
of radius r.

